24 Модуль деформации грунтов. Методы определения

МД ГР исп-ся в качестве деф-го пок-ля и хар-т упругие и остат деф-и. МД явл-ся важн хар-кой, исп-мой для расч основ-й и сооружений по деф-м. МД опр-ся в пол-х и лаб-х усл-х. Наиб распр-н способ лаборат опред - проведения компресс-х исп-й в одометрахс последующей их обработкой. В этом случае МД

E= β* (1+e(н))/m(0)

β— безразмерный коэффициент, определяемый в зависимости от коэффициента поперечного расширения v

β=1-2(ν^2)/(1-ν) – коэф расшир. ν-Пуас. .

где е — коэффициент пористости грунта в природном состоянии;

m0 - коэффициент сжимаемости (уплотнения) МП -1;

Для крупнообл-х ГР β = 0,8; песка и супесей - 0,74, сугл-в - 0,62, глин - 0,93.

Значение МД грунта, найденное с исп-м компр-х кривых, отл-ся от действ-го, так как при отборе образцов ГР происходит нарушение его природной структуры. Поэтому для опред-я МД исп-т полевой метод испытания грунта статической нагрузкой. По результатам испытаний строится график зависимости осадки от нагрузки

Рис. Испыт ГР стат нагр в шурфе. А- схема установки, Б – завис-ть ос-ки от инт-ти давл

1 – дно шурфа, 2 – нагр-ка,

3 – платформа, 4 – штамп.

Сущ-т так же прессиомет-рический метод (погруж в

скважину резинов цилиндр баллон, заполнен жидкостью).

Значение МД мо-но опред-ть так же на стабилометре. Иногда его прин-т по таблицам СниП (СНБ) исходя из простейших физическ характеристик грунта.

25 . Завис-ть между деф-и и напр-ми в условиях комп сж.

1 – ветвь сжатия, 2 – ветвь набухания.

e (i)=e(н) – (1+е(н))s(i)/h

е(i)=e(н) – p(i)tg(a), где

tg(a)=m(0) – коэф-т сжим-ти Г(МПа-1)

tg(a)=(e(н)-е(к))/(p(k)-p(н))

m(v)=m(0)/(1+e(н)) – коэф-т относит сжим-ти грунта

В усл-х компр-го сжатия появл-ся зав-ть между деф-ми и напряжениями, хар-ся МД-и (Е) и коэф-м сжим-ти (m0).

β=1-2(ν^2)/(1-ν) – коэф расшир. ν-Пуас.

E= β/m(ν) – модуль деформаций. E= β* (1+e(н))/m(0)

β— безразмерный коэффициент, определяемый в зависимости от коэффициента поперечного расширения v

m0 - коэффициент сжимаемости (уплотнения) МПа -1;

При провед компр-х испыт в одометрах образец грунта, наход-сь в жестк кольце, не м-т расш-ся в стор-ны. При этом он оказ-т на стенки кольца горизонт давление, кот-е соотв-т

гор-м напр-м σ(x)= σ(y). Вертик норм напр-е σ(z) = инт-ти прилож нагр-ки p(σ(z)=p). Поск-ку бок-е расшир отсут, относит горизонт деф-и ε(х)= ε(у)=0.

Т.к. в пред-х небольш измен давл ГР м-но рассм-ть, как лин деф-е тела, аналог-е выр-е м-но напис-ть и для зав-ти м-ду напр-ми и деф-ми гр-та в одометре. В таком сл-е имеем:

ε(х)= σ(x)/E(0)-(ν/E(0))/(σ(x)+ σ(z)).E – мод деф, ν- к Пуас.

Т.к σ(x)= σ(y), σ(z)= p, ε(x)=0 и произведя преобр получим:

σ(x)= σ(y)=(ν/(1- ν))*p=ξ*p. Где ξ – коэф-т бок давл грунта, при отсут гор-х перемещ.

26 Определение осадки методом послойного суммирования.

В методе послойного суммирования принят ряд допущений:

– осадка основания вызывается дополнительным давлением р₀, равным полному давлению под подошвой фундамента р за вычетом вертикального нормального напряжения от собственного веса грунта на уровне подошвы фундамента: р₀ = р – σ_zg,0 (при планировке срезкой принимается 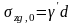, при отсутствии планировки или планировке подсыпкой 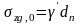, где – удельный вес грунта, расположенного выше подошвы; d и d_n – глубина заложения фундамента от уровня планировки и природного рельефа);

– распределение дополнительных вертикальных нормальных напряжений σ_zp от внешнего давления р₀ по глубине принимается по теории линейно-деформируемой среды как для однородного основания;

– при подсчете осадок основание делят на «элементарные» слои толщиной до 0,4b (b – ширина фундамента) и определяют сжатие их от дополнительного вертикального нормального напряжения σ_zp, действующего по оси фундамента в середине рассматриваемого слоя. Величина напряжения σ_zp на любой глубине определяется выражением , где α – коэффициент, зависящий от формы фундамента и относительной глубины рассматриваемой точки. Значения α приведены в таблице 1.9;

– положение нижней границы сжимаемой толщи принимается на глубине Н_с, где выполняется условие .

Если найденная по этому условию нижняя граница сжимаемой толщи попадает в слой грунта с модулем деформации Е < 5 МПа или такой слой залегает непосредственно ниже глубины Н_с, то нижняя граница сжимаемой толщи определяется исходя из условия .

Осадка фундамента s методом послойного суммирования определяется по формуле

где β – безразмерный коэффициент, равный 0,8; σ_zp,i – среднее значение дополнительного вертикального нормального напряжения в i-м слое грунта; h_i и Е_i – соответственно толщина и модуль деформации i-го слоя грунта; п – количество слоев, на которое разбита сжимаемая толща основания.