7.2 Задания для самостоятельной работы.

1. 1. № 223, № 224, № 230, № 238, № 242, № 295, № 299, № 320 [5]

2. Даны координаты вершин некоторого треугольника АВС. Найти:

а) уравнение стороны АВ; б) уравнение и длину высоты, проведенной из точки С; в) уравнение медианы, проведенной из точки А; г) точку пересечения медианы АЕ и высоты СД ; д) уравнение прямой, проходящей через точку С параллельно стороне АВ.

1. А(7; 1), В(-5; -4), С(-9; -2) 2. А(0; 5), В(12; 0), С(-8; 8)

3. А(8; 0), В(-4; -5), С(-8; 1) 4. А(1; 5), В(7; 0), С(-1; 8)

5. А(6; 1), В(-6; -4), С(2; 6) 6. А(-1; 5), В(5; 0), С(2; -8)

Рекомендуемая литература: [7] стр. 68-73, [4] стр. 31-38.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 8

Тема: Задачи на определение линий второго порядка на плоскости. Построение линий второго порядка.

8.1 Краткие сведения из теории и примеры решения задач.

Линии второго порядка

- уравнение окружности с центром в точке С(α;β) радиусом R.

– каноническое уравнение эллипса.

– каноническое уравнение гиперболы.

, – канонические уравнения параболы.

Уравнением кривой второго порядка в общем виде является выражение , левая часть которого есть многочлен второго порядка относительно х, у. При этом – квадратичная форма, – линейная форма, F – свободный член.

Пример 1.

Установить вид кривой второго порядка, заданной уравнением .

Преобразуем уравнение

, дополняя до полного квадрата слагаемые, содержащие х и у.

,

, разделим обе части уравнения на 16.

.

Обозначим , . Получим уравнение эллипса в системе координат , начало которой находится в точке О^/(3;-1): .

Построим обе системы координат и эллипс. Полуоси эллипса равны 4 и 2 (рис. 2).

Пример 2.

Составить уравнение и построить линию, каждая точка которой находится вдвое ближе к точке А(1;0), чем к точке В(-2;0).

Решение: Рассмотрим произвольную точку М(х;у), принадлежащую линии. Геометрическое свойство линии по условию задачи .Выразим это свойство через координаты точек А, В и М (рис. 3).

Е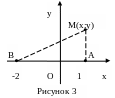 сли известны координаты двух точек М₁(х₁;у₁) и М₂(х₂;у₂) , то расстояние между ними определяется по формуле: . Используя эту формулу, находим:

;

.

Составляем уравнение для искомой линии , т.е

.

Преобразуем это уравнение. Возведем обе части в квадрат, раскроем скобки, приведем подобные члены, получим:

.

Дополним члены, содержащие х, до полного квадрата: ; .

Получили уравнение окружности с центром в точке С(2; 0) и радиусом r=2.

Построим эту окружность (рис. 4).

Пример 3.

П утем параллельного переноса системы координат привести уравнение кривой к каноническому виду. Построить обе системы координат и кривую

.

Решение: Преобразуем уравнение

.

Обозначим , . Получим .

Это уравнение параболы в системе координат , начало которой находится в точке О^'(1;2). Сделаем схематический чертеж (рис. 5).

8.2 Задания для самостоятельной работы.

1. Составить уравнение окружности в каждом из следующих случаев:

а) центр окружности совпадает с началом координат и ее радиус R=3;

б) центр окружности совпадает с точкой С(2; -3) и ее радиус R=7;

в) окружность проходит через начало координат и ее центр совпадает с точкой С(6; -8);

г) окружность проходит через три точки А(1; 1), В(1; -1) и С(2; 0).

2. № 385, № 397, № 398, № 444, № 447, № 449, № 471 [5]

3. № 517, № 541, № 584, № 596 – 598 [5]

4. Путем параллельного переноса системы координат привести уравнение к каноническому виду. Построить обе системы координат и кривую.

	а)	б)
	в)	г)
	д)	е)
	ж)	з)
	и)	к)

Рекомендуемая литература: [7] стр. 74-86, [4] стр. 41-56.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 9

Тема: Контрольная работа № 1

Контрольная работа выполняется по темам «Элементы линейной алгебры», «Элементы векторной алгебры», «Аналитическая геометрия на плоскости». Время выполнения 2 часа.

Примерные задания контрольной работы.

1. Решить систему линейных уравнений

2. Дано: вектор , две точки К(-6; 5; 1) и М(-6; 6; -2).

Найти:

а) длину вектора ;

б) координаты вектора ;

с) ;

д) скалярное произведение ;

е) векторное произведение .

3. Даны вершины треугольника А(6; 1), В(-6; 4) и С(-10; 2). Найти:

а) длину стороны АВ

б) уравнение и длину высоты, опущенной из вершины С

в) уравнение медианы, опущенной из вершины А

г) уравнение прямой, проходящей через точку С параллельно стороне АВ

4. Установить тип кривой, построить кривую .

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 10

Тема: Предел функции. Раскрытие неопределенностей , , .