2. Задания для самостоятельной работы.

1. Векторы заданы в пространстве своими координатами. Найти длину вектора .

а)	б)
в)	г)

2. № 372, № 373, № 387, № 398, № 396 [6]

3. № 749 – 752, № 754, № 758, № 775 – 778, № 782, № 785 [5]

Рекомендуемая литература: [7] стр. 39-45, [4] стр. 70-78.

Практическое занятие № 5

Тема: Скалярное произведение векторов. Векторное произведение векторов и его свойства. Смешанное произведение векторов.

5.1 Краткие сведения из теории и примеры решения задач.

Скалярное произведение векторов.

Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначается , ∙ . Итак, по определению , где .

Свойства скалярного произведения.

1. Скалярное произведение обладает переместительным свойством: .

2. Скалярное произведение обладает сочетательным свойством относительно скалярного множителя: .

3. Скалярное произведение обладает распределительным свойством: .

4. Скалярный квадрат вектора равен квадрату его длины: .

.

В частности: .

Если векторы и (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т.е. если , то . Справедливо и обратное утверждение: если и , то .

В частности: .

Скалярное произведение векторов равно сумме произведений их одноименных координат .

Некоторые приложения скалярного произведения

Угол между векторами

Определение угла φ между ненулевыми векторам и :

, т.е. .

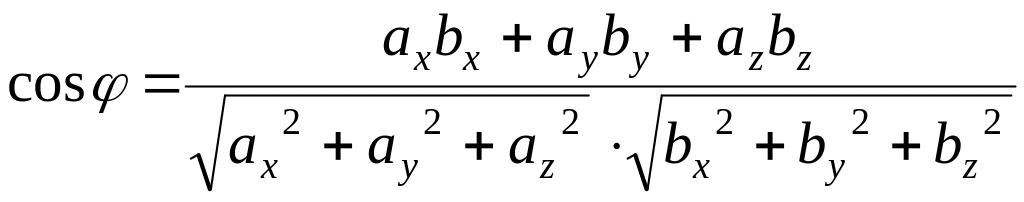Отсюда следует условие перпендикулярности ненулевых векторов и :

.

Работа постоянной силы

Пусть материальная точка перемещается прямолинейно из положения А в положение В под действием силы , образующей угол φ с перемещением .

И з физики известно, что работа силы при перемещении равна , т.е. . Таким образом, работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.

Пример 1. Вычислить работу, произведенную силой , если точка ее приложения перемещается прямолинейно из положения А(2;4;6) в положение В(4;2;7). Под каким углом к АВ направлена сила ?

Решение. Находим . Стало быть,

(ед. работы).

Угол φ между и находим по формуле .

, .

Пример 2. Векторы заданы в пространстве своими координатами. , , .

Найти: косинус угла между векторами и .

Решение.

Найдем векторы: ,

.

Найдем длины и скалярное произведение векторов:

,

,

.

Косинус угла между полученными векторами находим по формуле

.

Векторное произведение векторов

В екторным произведением вектора на вектор называется вектор , который:

1) перпендикулярен векторам и , т.е. и ;

2) имеет длину, численно равную произведению модулей векторов и на синус угла между ними т.е. , где ;

3) векторы , и образуют правую тройку.

Векторное произведение обозначается × или .

Из определения векторного произведения непосредственно вытекаеют следующие соотношения между ортами , и : , , .

Свойства векторного произведения.

1. При перестановке сомножителей векторное произведение меняет знак, т.е. .

2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т.е. .

3. Два ненулевых вектора и коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т.е. || .

В частности .

Векторное произведение обладает распределительным свойством:

.

Выражение векторного произведения через координаты.

или .

Некоторые приложения векторного произведения.

Установление коллинеарности векторов.

Если || , то (и наоборот), т.е.

|| .

Нахождение площади параллелограмма или треугольника.

Согласно определению векторного произведения векторов и , т.е. . И, значит, .

Пример. Даны координаты трех точек А(2; -1; -2), В(1; 2; 1), С(2; 3; 0). Найти косинус угла при вершине А, площадь треугольника АВС.

Решение. Найдем координаты векторов , .

1. Косинус угла находим по формуле

.

2. Площадь треугольника АВС вычисляем, используя формулу .

Находим векторное произведение:

Находим площадь:

(кв.ед.).

Смешанное произведение векторов

Смешанным произведением векторов называется скалярное произведение вектора на вектор . Смешанное произведение обозначается или и представляет собой некоторое число.

Выражение смешанного произведения через координаты.

Пусть заданы векторы , , . Смешанное произведение векторов вычисляется по формуле .

Некоторые приложения смешанного произведения.

1. Определение взаимной ориентации векторов в пространстве: если , то - правая тройка, если , то – левая тройка.

2. Установление компланарности векторов: векторы компланарны тогда и только тогда, когда их смешанное произведение равно нулю ( ).

векторы компланарны.

Объем параллелепипеда, построенного на векторах вычисляется как , а объем треугольной пирамиды, построенной на этих же векторах, равен .

Пример. Вершинами пирамиды служат точки А(1;2;3), В(0;-1;1), С(2;5;2) и D(3;0;2). Найти объем пирамиды.

Решение. Находим векторы .

.

Находим :

.

Следовательно, куб. ед.