3.2 Задания для самостоятельной работы.

Решить систему уравнений по формулам Крамера и методом Гаусса.

1. Ответ: х=1; y=5; z=-2.

5. № 1236-1243, № 1244-1246. [5]

6. № 615 - № 622. [6]

Индивидуальная домашняя работа по теме «Системы линейных уравнений»

1. Решить систему уравнений тремя методами: с помощью формул Крамера, методами матричного исчисления, методом Гаусса. (N- номер варианта, указывает преподаватель)

а) б)

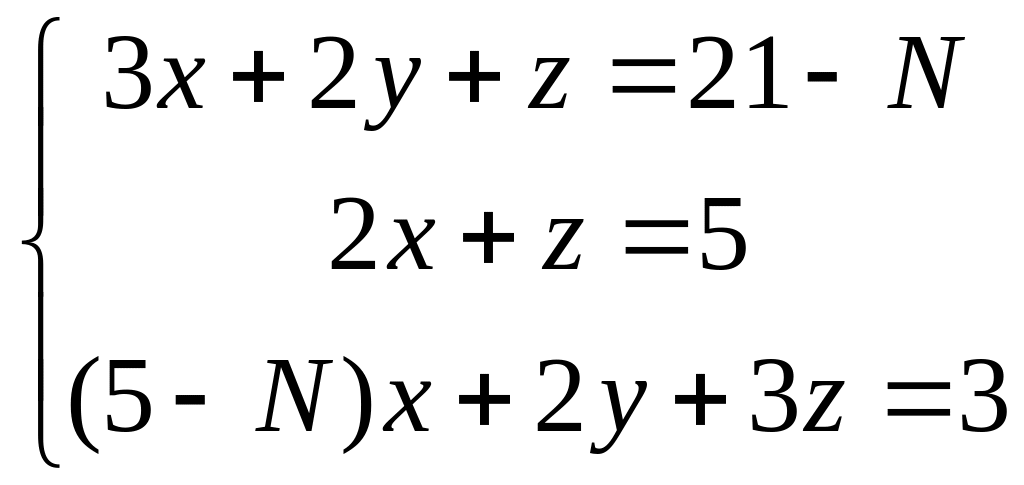
2. Решить систему линейных уравнений с помощью формул Крамера и методом Гаусса.

Рекомендуемая литература: [7] стр. 32-37, [4] стр. 65-69.

Практическое занятие № 4 Тема: Векторы. Действия над векторами, заданными проекциями.

1. Краткие сведения из теории и примеры решения задач.

Векторы

Вектор – это направленный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. Обозначается символом или .

Длина отрезка АВ называется длиной или модулем вектора и обозначается .

Вектор, длина которого равна единице, называется единичным вектором и обозначается . Единичный вектор называют ортом.

Два вектора называются равными, если они параллельны, направлены в одну сторону и имеют одинаковые длины.

Векторы и , параллельные одной и той же прямой, называются коллинеарными.

Векторы, лежащие в одной плоскости или в параллельных плоскостях, называются компланарными.

Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.

Формула

является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа а_х ,а_у и а_z называются координатами вектора, т.е. координаты вектора есть его проекции на соответствующие координатные оси. Это векторное равенство часто записывают в символическом виде .

Зная проекции вектора , можно легко найти модуль вектора и направляющие косинусы:

;

, , .

Числа , , называются направляющими косинусами вектора . Для направляющих косинусов справедливо соотношение

.

Действия над векторами, заданными координатами

Пусть векторы и заданы своими проекциями на оси координат Ох, Оу, Оz или, что то же самое

.

Линейные операции над векторами

1. ,

или коротко . То есть при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).

2. или короче .

То есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.

Равенство векторов

Два вектора и равны тогда и только тогда, когда выполняются равенства , т.е.

.

Коллинеарность векторов

или .

Проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: векторы, имеющие пропорциональные координаты, коллинеарны.

Координаты вектора, заданного точками

Если известны координаты точек А(х₁;у₁;z₁) и В(х₂;у₂;z₂), то координаты вектора равны разностям соответствующих координат его конца и начала: .

Пример 1. Даны точки А₁(2; -1; -2), А₂(1; 2; 1). Найти модуль вектора и направляющие косинусы.

Решение.

Найдем координаты вектора . Находим модуль и направляющие косинусы , , , .

Пример 2. Векторы заданы в пространстве своими координатами. , , .

Найти: длину вектора .

Решение.

Найдем векторы: , , .

Выполним сложение:

.

Найдем модуль (длину) полученного вектора

лин. ед.