Решение систем линейных алгебраических уравнений матричным методом
Рассмотрим систему из трех уравнений с тремя неизвестными (m=n):
Матрица
,
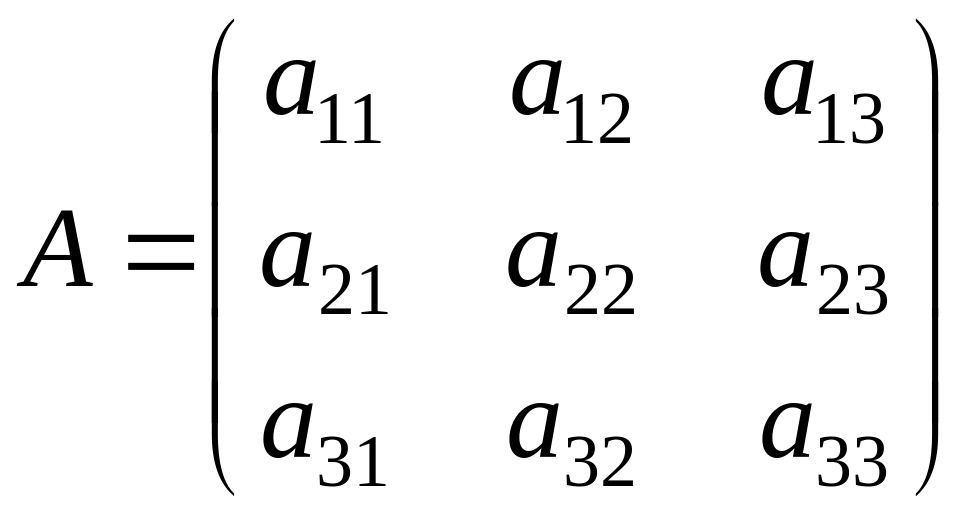составленная из коэффициентов, стоящих
перед неизвестными, называется матрицей
системы или главной матрицей.
-
матрица-столбец неизвестных,
-
матрица-столбец свободных членов.
Систему алгебраических уравнений можно
представить в виде матричного уравнения
.
Это уравнение имеет решение, если матрица
А невырожденная , т.е.
.
В этом случае для матрицы А существует
обратная А-1. Умножим
матричное уравнение слева на матрицу
А-1 .
,
так как
,
то получаем
- решение матричного уравнения.
Таким образом, чтобы найти матрицу неизвестных Х, надо найти обратную матрицу к главной матрице А и умножить ее на матрицу свободных членов В.
.
Пример: Пусть дана система уравнений
.
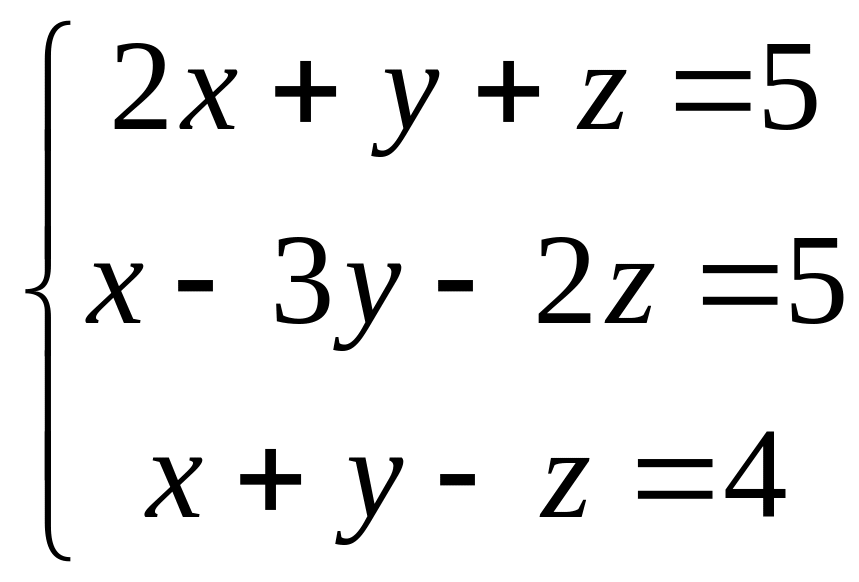Обозначим
.
Находим определитель главной матрицы:
Для отыскания обратной матрицы находим алгебраические дополнения
Составляем обратную матрицу
Находим неизвестную матрицу Х:
.
Ответ:
Сделаем проверку. Подставив в каждое уравнение системы полученные значения неизвестных, должны получить тождества.
2.2 Задания для самостоятельной работы:
Найти обратные матрицы к данным, сделать проверку.
1.
.
2.
.
3.
.
Ответ:
,
4.
.
Ответ:
.
Решить систему уравнений матричным методом.
Ответ: х=1; y=5;
z=-2.
№ 1238, № 1239, № 1240 [5]
Рекомендуемая литература: [3] стр. 522-538, [7] стр. 24, 29-30.
Практическое занятие № 3 Тема: Решение систем линейных алгебраических уравнений с помощью формул Крамера и методом Гаусса.
3.1 Краткие сведения из теории и примеры решения задач.
Метод Крамера
Теорема Крамера. Если определитель
матрицы системы n-го
порядка отличен от нуля
,
то система совместна и имеет единственное
решение, которое определяется по формулам
.
-
вспомогательный определитель, полученный
из главного путем замены столбца
коэффициентов при хi
на столбец свободных членов. В
частности, для матрицы 3-го порядка
.
Пример. Решить систему уравнений с помощью формул Крамера:
Находим определитель системы и вспомогательные определители:
Находим неизвестные по формулам Крамера:
Решение систем линейных уравнений методом Гаусса.
Наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, в основе которого лежит идея последовательного исключения неизвестных из уравнений системы. Методом Гаусса решаются произвольные системы.
Рассмотрим для примера конкретную систему третьего порядка:
Переставим уравнения 1 и 2 (так удобнее для вычислительного процесса):
Из второй строки вычтем первую, умноженную на 3 (коэффициент при х), а из третьей – первую, умноженную на 4 (также коэффициент при х в третьем уравнении), получим систему уравнений, в которой неизвестная величина х присутствует только в первом уравнении (уже отсюда ясно, для чего в первом уравнении исходной системы коэффициент при х желательно иметь равным единице – удобнее подбирать множители перед вычитанием из последующих уравнений)
.
Затем вторую строку умножим на 5 и вычтем из третьей
.
В итоге получаем систему ступенчатого типа, решение которой (начиная с последнего уравнения) не представляет труда.
Получаем:
Замечания:
1. Для удобства вычислений в качестве первого уравнения и исключаемого неизвестного удобно взять то, где коэффициент аij=1.
2. Практически удобнее приводить к ступенчатому виду не саму систему уравнений, а матрицу из коэффициентов при неизвестных и свободных членов. Вычитание строк матриц равносильно вычитанию уравнений. Такая матрица обычно называется расширенной.
С помощью метода Гаусса можно установить, совместна система или несовместна:
- если при последовательном исключении
переменных получили хотя бы одно
уравнение вида 0=b,
т.е.
(
),
то система несовместна;
- если получили уравнение вида 0=0, т.е.
,
то система является совместной и
неопределенной, т.е. имеет множество
решений.
Пример: Найти все решения системы линейных уравнений
Определитель главной матрицы равен
нулю
.
Систему решим методом Гаусса.
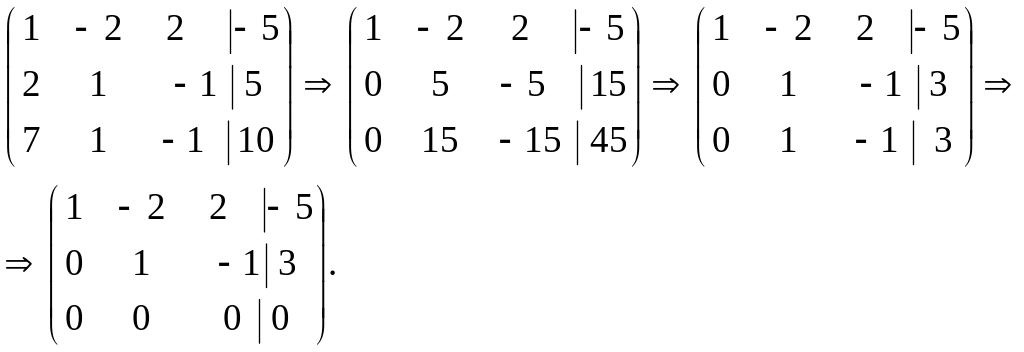
Очевидно, что такая система допускает множество решений.
Из второй строки имеем:
.
Из первой строки:
.
Получили множество решений:
,
z –любое
действительное число. Получим несколько
частных решений: z=1,
x=1, y=4;
z=-1, x=1,
y=2.