Свойства определителей:

1. Определитель не изменится, если его строки заменить столбцами и наоборот.

2. При перестановке двух соседних строк (столбцов) определитель меняет знак на противоположный.

3. Определитель с двумя одинаковыми строками (столбцами) равен 0.

4. Общий множитель всех элементов некоторой строки (столбца) определителя можно вынести за знак определителя.

5. Определитель не изменится, если к элементам одного из его столбцов (строки) прибавить соответствующие элементы любого другого столбца (строки), умноженные на некоторое число.

1Если некоторый столбец (или строка) состоит из нулей, то определитель равен 0.

2. Задания для самостоятельной работы

1. . Найти .

2. . Найти .

3. . Найти .

4. . Можно ли данные матрицы сложить, умножить?

5. Найти линейную комбинацию матриц 2А+3В, где

. Ответ:

6. Дано . Найти произведение АВ и ВА.

Ответ: ; ВА – не существует.

6. Найти произведение матриц АА^Т и А^ТА.

Ответ: , .

8. Вычислить определители данных матриц.

а) б)

в) г)

9. Вычислить определители:

а) б) в)

Ответ: а) -3; б) 2; в) 63.

10. № 586 - № 593, № 596, № 597. [6]

11. № 1204, № 1211- № 1216, №1252-1255. [5]

Рекомендуемая литература: [7] стр. 16-22, [4] стр. 60-64.

Практическое занятие № 2

Тема: Обратная матрица. Матричный метод решения систем линейных алгебраических уравнений.

2.1 Краткие сведения из теории и примеры решения задач.

Обратная матрица

Пусть А квадратная матрица n–го порядка.

Квадратная матрица А называется невырожденной, если ее определитель не равен нулю (Δ≠0). В противном случае (Δ=0) матрица называется вырожденной.

Присоединенной матрицей к матрице А, называется матрица

, где А_ij – алгебраическое дополнение элемента а_ij данной матрицы А.

А^* получается транспонированием матрицы, составленной из алгебраических дополнений А_ij к элементам а_ij (А^*=(А_ij)^Т).

Квадратная матрица А^-1 называется обратной по отношению к матрице А того же порядка, если выполняется условие АА^-1 = А^-1А = Е.

Обратная матрица определяется по формуле .

Алгоритм вычисления элементов обратной матрицы А^-1 таков:

1. Вычисляем определитель матрицы А, ΔА≠0.

2. Вычисляем алгебраическое дополнение к каждому элементу матрицы А.

3. Составляем матрицу из алгебраических дополнений (А_ij).

4. Транспонировав полученную матрицу, получаем присоединенную матрицу А^*=(А_ij)^Т.

5. Все элементы матрицы а* делим на величину определителя матрицы а.

Пример. Найти матрицу, обратную заданной матрице А:

;

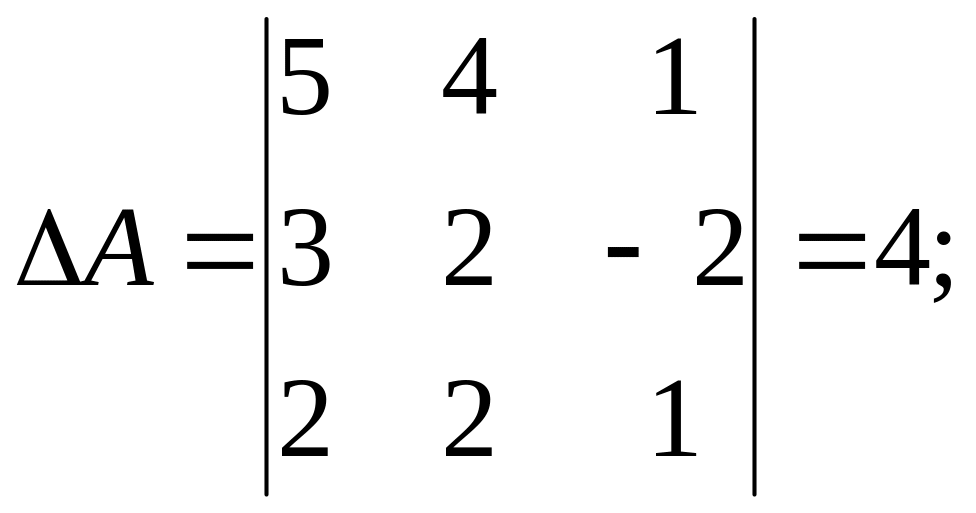
Вычислим алгебраические дополнения:

Составляем присоединенную матрицу и находим обратную:

; .

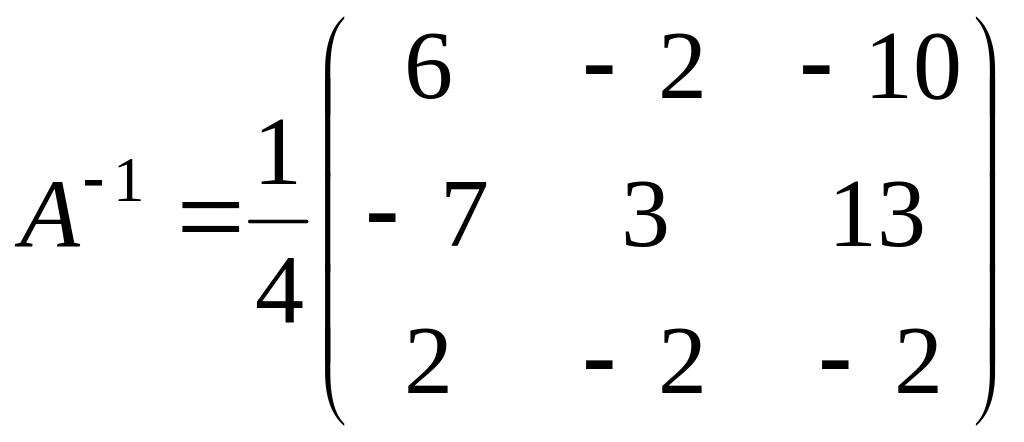Проверку правильности нахождения обратной матрицы легко выполнить, учитывая, что произведение исходной матрицы на обратную дает единичную матрицу, т.е. АА^-1 = А^-1А = Е.

Проверка:

Замечание. Нахождение обратной матрицы второго порядка (и только второго порядка) можно выполнить следующим простым способом:

1. найти определитель исходной матрицы А;

2. в исходной матрице А поменять местами элементы, стоящие на главной диагонали, изменить знаки на противоположные у элементов побочной диагонали, т.е. получить присоединенную матрицу.

3. Разделить элементы присоединенной матрицы на величину определителя.

Например, если , то и .