21.1 Краткие сведения из теории и примеры решения задач.

Мнимой единицей называется число, квадрат которого равен -1. Обозначается .

Комплексным числом называется выражение , где х и у действительные числа, i - мнимая единица. Если х=0, то называется чисто мнимым числом, если у=0, то является действительным числом, т.е. множество R действительных чисел является подмножеством множества комплексных чисел С ( ).

Комплексные числа и называются сопряженными.

Сложение, вычитание, умножение комплексных числе осуществляется по правилам действия над многочленами. После каждого действия выделяют действительную и мнимую часть. Пусть ;

1.

2.

В частном случае, когда z₁ и z₂ сопряженные числа, получим: , т.е. произведение двух сопряженных чисел равно действительному числу. Этим пользуются при делении комплексных чисел.

3. При делении комплексных чисел числитель и знаменатель следует умножить на число, сопряженное знаменателю, и в полученном результате выделить действительную и мнимую часть.

_{Различные формы комплексных чисел.}

- алгебраическая форма комплексного числа.

- тригонометрическая форма комплексного числа, где r - модуль, φ - аргумент комплексного числа.

показательная форма комплексного числа.

Пример 1. Записать в тригонометрической и показательной форме следующие комплексные числа: а) ; б) ; в) .

Решение.

а)

_{Изобразим данное число на комплексной плоскости (рис. 11).}

_{Н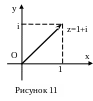 айдем модуль и аргумент этого комплексного числа.}

_{Аргумент комплексного числа удобно определить из формул:}

Угол, для которого , находится в первой четверти .

Итак, данное число можно записать в следующей тригонометрической форме .

Показательная форма: .

б) z=-2 ; x=-2; y=0. (рис. 12).

Тригонометрическая форма данного числа: .

П оказательная форма: .

в) (рис. 12).

Тригонометрическая форма: .

Показательная форма: .

Пример 2. Дано комплексное число .

1) Записать это число в алгебраической, тригонометрической и показательной формах.

Решение.

1) Чтобы записать число z в алгебраической форме , умножим числитель и знаменатель на число, сопряженное знаменателю

.

Итак, алгебраическая форма числа: .

Запишем данное число в тригонометрической форме .

И меем . Получим ,

Угол, для которого косинус положителен, а синус отрицателен, находится в четвертой четверти. В этом можно убедиться, если изобразить данное число на комплексной плоскости (рис. 13). Следовательно, .

Число z в тригонометрической форме запишется в виде .

Показательная форма: .

2. Задания для самостоятельной работы.

1. Выполнить действия

а) б)

в) г)

2. Дано комплексное число z. Требуется: записать число z в алгебраической, тригонометрической и показательной форме, изобразить число на комплексной плоскости.

а)		б)
в)		г)
д)		е)

3. № 631, № 632, № 633, № 650, № 651, № 652 [6]

Рекомендуемая литература: [2] стр. 218-225, [7] стр. 218-224.

ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭЕКЗАМЕНУ

1. Определители, их вычисление и свойства.

2. Матрицы. Виды матриц. Сложение, умножение матриц.

3. Минор. Алгебраическое дополнение. Обратная матрица. Алгоритм нахождения обратной матрицы.

4. Решение систем линейных алгебраических уравнений матричным методом.

5. Решение системы линейных алгебраических уравнений с помощью формул Крамера и методом Гаусса.

6. Скалярное произведение двух векторов. Нахождение угла между двумя векторами.

7. Векторное произведение двух векторов. Смешанное произведение векторов.

8. Расстояние между двумя точками на плоскости.

9. Уравнение прямой с угловым коэффициентом.

10. Уравнение прямой, проходящей через данную точку и уравнение прямой в отрезках на осях.

11. Уравнение прямой, проходящей через две заданные точки.

12. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых.

13. Линии второго порядка. Уравнение окружности.

14. Каноническое уравнение эллипса и его основные соотношения.

15. Канонические уравнения гиперболы и параболы.

16. Предел функции. Бесконечно большие и бесконечно малые величины.

17. Первый замечательный предел.

18. Второй замечательный предел.

19. Частные случаи вычисления пределов.

20. Непрерывность функций. Точки разрыва их классификация.

21. Производная, ее геометрический и механический смыл.

22. Производная суммы, произведения и частного двух функций.

23. Производные элементарных функций.

24. Производные сложных, неявных и параметрически заданных функций.

25. Производные обратных функций.

26. Производные высших порядков.

27. Правило Лопиталя.

28. Нахождение экстремумов функций и их асимптот.

29. Выпуклость и вогнутость кривых. Точки перегиба.

30. Исследование графиков функций.

31. Понятие о функции нескольких переменных.

32. Частные производные функции нескольких переменных.

33. Метод наименьших квадратов.

34. Понятие комплексного числа. Алгебраическая и тригонометрическая формы комплексных чисел.

35. Сложение, умножение комплексных чисел. Возведение в степень. Формула Муавра.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 –х ч. Ч. I: Учеб. пособие для втузов./П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова – Москва: ОНИКС: Мир и Образование, 2009 – 368с.

2. Пискунов Н.С. Дифференциальное и интегральное исчисления. В 2-х томах, том 1: учеб. пособие для втузов./ Н.С. Пискунов – М.: изд. «Наука», 1972 .– 456 с.

3. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. В 2-х томах, том 2: учеб. Пособие для втузов../ Н.С. Пискунов –М.: изд. «Наука»,1972 .– 456 с.

4. Слободская В.А. Краткий курс высшей математики. Изд. 2-е, переработ. и доп. Учеб. пособие для втузов./ В.А. Слободская – М.: Высш. шк., 1969.– 544с.

5. Клетеник Д.В. Сборник задач по аналитической геометрии: Уч. пособие для втузов./ Д.В.Клетеник – СПб., Изд-во «Профессия», 2007. – 199 стр., ил.

6. Минорский В.П. Сборник задач по высшей математике./В.П. Минорский – М.: изд. «Наука», 1969.- 352 с.:ил.

Дополнительная литература:

7. Письменный Д.Т. Конспект лекций по высшей математике: полный курс.–4-е изд./ Д.Т. Письменный –М.: Айрис-пресс, 2006.–608 с. – (Высшее образование).

8. Каплан И.А. Практические занятия по высшей математике. Часть 1,2./ И.А. Каплан - Издательство Харьковского государственного университета, 1966 г., 236 с.

© Ирина Александровна Драчева

Методические указания (часть 1)

к практическим занятиям

для студентов дневной и заочной форм обучения

направления 26.05.06 «Эксплуатация судовых энергетических установок»

Тираж ___экз. Подписано к печати ________________________

Заказ № ___________. Объем 2,1 п.л.

Изд-во «Керченский государственный морской технологический университет»