
- •Драчева и.А. Математика
- •Часть 1
- •Методические указания
- •Содержание
- •Краткие сведения из теории и примеры решения задач.
- •Основные типы матриц:
- •Умножение матрицы на число. Все элементы исходной матрицы умножаются на заданное число. Например, .
- •Определители. Вычисление определителей.
- •Свойства определителей:
- •1Если некоторый столбец (или строка) состоит из нулей, то определитель равен 0.
- •Задания для самостоятельной работы
- •Практическое занятие № 2
- •2.1 Краткие сведения из теории и примеры решения задач.
- •5. Все элементы матрицы а* делим на величину определителя матрицы а.
- •Решение систем линейных алгебраических уравнений матричным методом
- •2.2 Задания для самостоятельной работы:
- •Практическое занятие № 3 Тема: Решение систем линейных алгебраических уравнений с помощью формул Крамера и методом Гаусса.
- •3.1 Краткие сведения из теории и примеры решения задач.
- •Решение систем линейных уравнений методом Гаусса.
- •3.2 Задания для самостоятельной работы.
- •Индивидуальная домашняя работа по теме «Системы линейных уравнений»
- •Практическое занятие № 4 Тема: Векторы. Действия над векторами, заданными проекциями.
- •Краткие сведения из теории и примеры решения задач.
- •Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
- •Задания для самостоятельной работы.
- •Практическое занятие № 5
- •5.1 Краткие сведения из теории и примеры решения задач.
- •5.2 Задания для самостоятельной работы.
- •6.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •7.1 Краткие сведения из теории и примеры решения задач.
- •7.2 Задания для самостоятельной работы.
- •8.1 Краткие сведения из теории и примеры решения задач.
- •8.2 Задания для самостоятельной работы.
- •10.1 Краткие сведения из теории и примеры решения задач.
- •10.2 Задания для самостоятельной работы.
- •11.1 Краткие сведения из теории и примеры решения задач.
- •11.2 Задания для самостоятельной работы.
- •12.1 Краткие сведения из теории и примеры решения задач.
- •12.2 Задания для самостоятельной работы.
- •13.1 Краткие сведения из теории и примеры решения задач.
- •13.2 Задания для самостоятельной работы
- •14.1 Краткие сведения из теории и примеры решения задач.
- •14.2 Задания для самостоятельной работы
- •15.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •16.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •17.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •18.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •Краткие сведения из теории и примеры решения задач.
- •19.2 Задания для самостоятельной работы
- •21.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •98309, Г. Керчь, Орджоникидзе, 82
Задания для самостоятельной работы.
Найти экстремумы функции, интервалы убывания, возрастания функции.
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
д)
![]() е)
е)
![]()
2. Найти интервалы выпуклости, вогнутости, точки перегиба
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
3. Найти наименьшее и наибольшее значение
функции
на отрезке
![]() .
.
-
а)
 [1; 4]
[1; 4]б)
 [1; 9]
[1; 9]в)
 [1; 4]
[1; 4]г)
 [0;
[0;
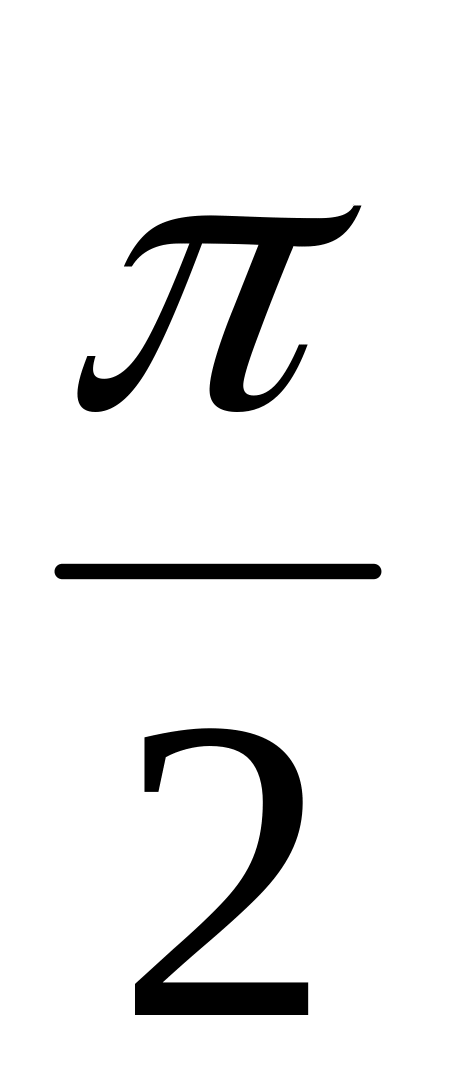 ]
]д)
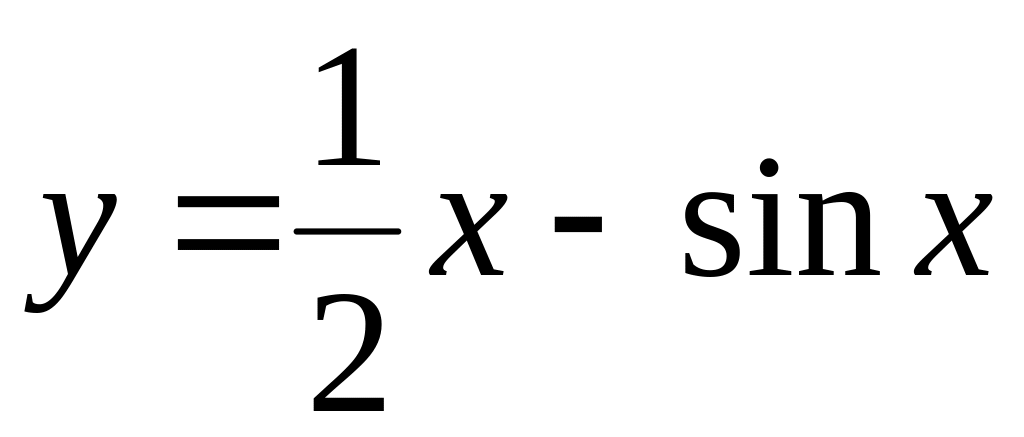 [0;
]
[0;
]е)
 [0; 4]
[0; 4]ж)
 [-4; -1]
[-4; -1]з)
 [1; 4]
[1; 4]
4. № 1055, № 1058, № 1060, № 1064, № 1067, № 1086 [1]
Рекомендуемая литература: [2] стр. 152-167, 172, [7] стр. 200-211, [4] стр. 226-253.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 18
Тема: Функции двух переменных. Частные производные.
18.1 Краткие сведения из теории и примеры решения задач.
Пусть даны два непустых множества D
и V. Если каждой паре
действительных чисел (x,
y) из множества
D по некоторому правилу
ставится в соответствие определенный
элемент z из множества
V, то говорят, что на
множестве D задана
функция. Ее обозначают
![]() .
.
При этом x и y называются независимыми переменными (аргументами) , а z – зависимой переменной (функцией). D – область определения функции, V –множество ее значений.
Если существует конечный предел
![]() ,
то он называется частной производной
функции
по
независимой переменной x.
Вычисляется в предположении, что y
- постоянная. Обозначается
,
то он называется частной производной
функции
по
независимой переменной x.
Вычисляется в предположении, что y
- постоянная. Обозначается
![]()
Если существует конечный предел
![]() ,
то он называется частной производной
функции
по
независимой переменной y.
Вычисляется в предположении, что x
- постоянная. Обозначается
,
то он называется частной производной
функции
по
независимой переменной y.
Вычисляется в предположении, что x
- постоянная. Обозначается
![]()
Частные производные находят по формулам и правилам вычисления производных функции одной переменной.
Пример1.
![]() .
Найти
.
Найти
![]() и
и
![]() .
.
Решение. Рассматривая y как постоянную, получим:
![]() .
.
В предположении, что x постоянная, находим частную производную по у:
![]() .
.
Пример 2.
![]() .
Найти
и
.
.
Найти
и
.
Решение.
![]()
![]() .
.
Пример 3.
![]() .
Найти
и
.
.
Найти
и
.
Решение.
![]()
![]() .
.
Задания для самостоятельной работы.
№ 1197 – 1200, № 1203, № 1216, № 1219 [1]
№ 1230 - 1235, № 1238, № 1241, № 1278 [1]
Найти частные производные первого и второго порядка:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
д)
![]() е)
е)
![]()
4. Найти частную производную
![]() функции
функции
![]()
5. Найти частную производную
![]() функции
функции
![]()
6. Найти частную производную
![]() функции
функции
![]()
7. Найти частную производную
![]() функции
функции
![]()
8. Найти частную производную
![]() функции
функции
![]()
9. Найти частную производную
функции
![]()
10. Найти частную производную
функции
![]()
Рекомендуемая литература: [2] стр. 243-253, [7] стр. 304-310, [4] стр. 414-418.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 19
Тема: Полный дифференциал функции двух переменных. Дифференцирование неявной функции. Построение эмпирических формул методом наименьших квадратов.
