
- •Драчева и.А. Математика
- •Часть 1
- •Методические указания
- •Содержание
- •Краткие сведения из теории и примеры решения задач.
- •Основные типы матриц:
- •Умножение матрицы на число. Все элементы исходной матрицы умножаются на заданное число. Например, .
- •Определители. Вычисление определителей.
- •Свойства определителей:
- •1Если некоторый столбец (или строка) состоит из нулей, то определитель равен 0.
- •Задания для самостоятельной работы
- •Практическое занятие № 2
- •2.1 Краткие сведения из теории и примеры решения задач.
- •5. Все элементы матрицы а* делим на величину определителя матрицы а.
- •Решение систем линейных алгебраических уравнений матричным методом
- •2.2 Задания для самостоятельной работы:
- •Практическое занятие № 3 Тема: Решение систем линейных алгебраических уравнений с помощью формул Крамера и методом Гаусса.
- •3.1 Краткие сведения из теории и примеры решения задач.
- •Решение систем линейных уравнений методом Гаусса.
- •3.2 Задания для самостоятельной работы.
- •Индивидуальная домашняя работа по теме «Системы линейных уравнений»
- •Практическое занятие № 4 Тема: Векторы. Действия над векторами, заданными проекциями.
- •Краткие сведения из теории и примеры решения задач.
- •Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
- •Задания для самостоятельной работы.
- •Практическое занятие № 5
- •5.1 Краткие сведения из теории и примеры решения задач.
- •5.2 Задания для самостоятельной работы.
- •6.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •7.1 Краткие сведения из теории и примеры решения задач.
- •7.2 Задания для самостоятельной работы.
- •8.1 Краткие сведения из теории и примеры решения задач.
- •8.2 Задания для самостоятельной работы.
- •10.1 Краткие сведения из теории и примеры решения задач.
- •10.2 Задания для самостоятельной работы.
- •11.1 Краткие сведения из теории и примеры решения задач.
- •11.2 Задания для самостоятельной работы.
- •12.1 Краткие сведения из теории и примеры решения задач.
- •12.2 Задания для самостоятельной работы.
- •13.1 Краткие сведения из теории и примеры решения задач.
- •13.2 Задания для самостоятельной работы
- •14.1 Краткие сведения из теории и примеры решения задач.
- •14.2 Задания для самостоятельной работы
- •15.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •16.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •17.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •18.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •Краткие сведения из теории и примеры решения задач.
- •19.2 Задания для самостоятельной работы
- •21.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •98309, Г. Керчь, Орджоникидзе, 82
Задания для самостоятельной работы.
Вычислить предел функции с помощью правила Лопиталя.
 5.
5.
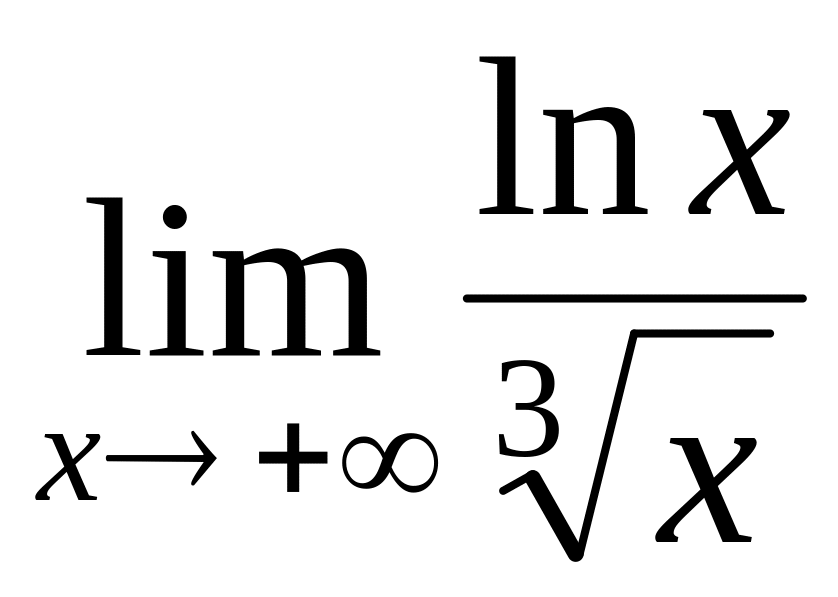
 6.
6.

 7.
7.

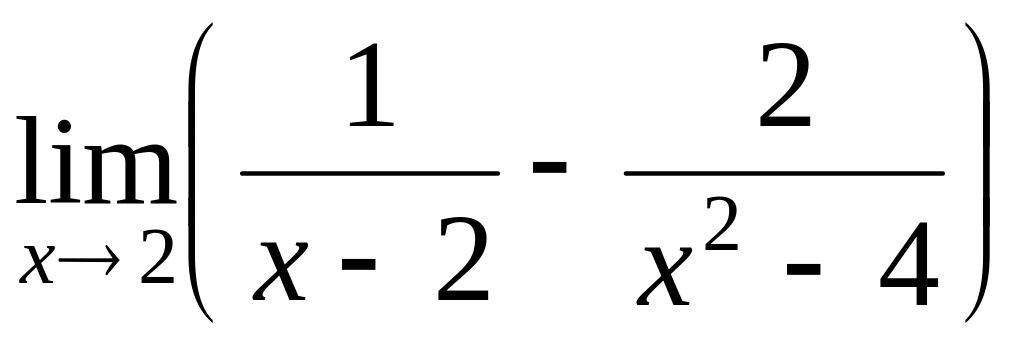 8.
8.

Составить уравнение касательной и
нормали к кривой
в точке с абсциссой
![]() .
.
1.
![]() ,
,
2.
![]() ,
,
![]()
3.
![]() ,
,
![]()
4.
![]() ,
,
![]()
5.
![]() ,
,
![]()
Задачи на физический смысл производной:
№ 931, № 933 [1]
№ 1090, № 1091, № 1096, № 1099 [6]
Рекомендуемая литература: [2] стр. 70, 117-119,135-138, [7] стр. 164, 183 196, [4] стр. 192,236.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 17
Тема: Экстремумы функций. Интервалы возрастания и убывания, выпуклости, вогнутости. Наибольшее, наименьшее значение функции на отрезке.
17.1 Краткие сведения из теории и примеры решения задач.
Функция
называется
возрастающей в интервале
![]() ,
если для любых двух точек
,
если для любых двух точек
![]() и
и
![]() из указанного интервала, удовлетворяющих
неравенству
из указанного интервала, удовлетворяющих
неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() ,
если
,
если
![]() ,
функция называется неубывающей.
,
функция называется неубывающей.
Иными словами – значения возрастающей функции увеличиваются одновременно со значением аргумента.
Функция
называется убывающей в интервале
,
если для любых двух точек
и
из указанного интервала, удовлетворяющих
неравенству
,
выполняется неравенство
![]() ,
если
,
если
![]() ,
функция называется невозрастающей.
,
функция называется невозрастающей.
Признаки монотонности функции:
- если функция
дифференцируема на интервале
и
![]() во всех точках интервала, то функция
возрастает на этом интервале;
во всех точках интервала, то функция
возрастает на этом интервале;
- если функция
дифференцируема на интервале
и
![]() во всех точках интервала, то функция
убывает на этом интервале.
во всех точках интервала, то функция
убывает на этом интервале.
Пример. Исследовать функцию
![]() на возрастание, убывание.
на возрастание, убывание.
![]()
![]() на интервалах
на интервалах
![]() ,
следовательно, на этом промежутке
функция возрастает (знак производной
«+»).
,
следовательно, на этом промежутке
функция возрастает (знак производной
«+»).
![]() на интервале (-1;1), следовательно, функция
здесь убывает (знак производной «–»).
на интервале (-1;1), следовательно, функция
здесь убывает (знак производной «–»).
Экстремумы функции.
Точка
называется точкой максимума функции
,
если значение
![]() является
наибольшим в некоторой окрестности
этой точки.
является
наибольшим в некоторой окрестности
этой точки.
Точка
называется точкой минимума функции
,
если значение
![]() является
наименьшим в некоторой окрестности
этой точки.
является
наименьшим в некоторой окрестности
этой точки.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках – экстремумами функции.
Если
- точка экстремума для функции
,
то в этой точке производная функции
либо равна нулю
![]() ,
либо не существует.
,
либо не существует.
Если при переходе (слева направо) через
критическую точку
производная
![]() меняет знак с (+) на (-), то точка
является точкой максимума; если с (-) на
(+), то точкой минимума; если знака не
меняет, то экстремума нет.
меняет знак с (+) на (-), то точка
является точкой максимума; если с (-) на
(+), то точкой минимума; если знака не
меняет, то экстремума нет.
Правило исследования функции на экстремум:
Найти критические точки функции . Для этого решить уравнение
 ;
;Выбрать из них лишь те точки, которые являются внутренними точками области определения функции;
Исследовать знак производной слева и справа от каждой из выбранных точек;
Вычислить значение функции в выбранных точках.
Пример. Найти экстремум функции
![]() .
.
Область определения функции:
 ;
; ,
производная равна нулю в точке х=8
и не существует в точке х=0. Критические
точки х=0 и х=8.
,
производная равна нулю в точке х=8
и не существует в точке х=0. Критические
точки х=0 и х=8.Определяем знак производной в интервалах
 .
.

Точка х=0 – точка максимума,
точка х=8 – точка минимума.
![]() ,
,
![]() .
.
Выпуклость и вогнутость функции. Точки перегиба.
Г
 рафик
функции называется выпуклым в интервале
,
если он расположен ниже касательной,
проведенной в любой точке этого интервала
(рисунок 7).
рафик
функции называется выпуклым в интервале
,
если он расположен ниже касательной,
проведенной в любой точке этого интервала
(рисунок 7).
График функции называется вогнутым в интервале , если он расположен выше касательной, проведенной в любой точке этого интервала (рисунок 8).
Пусть функция
имеет вторую производную на интервале
.
Тогда, если
![]() на этом интервале, то функция выпукла,
если
на этом интервале, то функция выпукла,
если
![]() ,
то график функции вогнутый на этом
интервале.
,
то график функции вогнутый на этом
интервале.
Точка графика непрерывной функции , отделяющая его части выпуклости и вогнутости, называется точкой перегиба (рисунок 9).
Если
– точка перегиба функции
,
то в этой точке вторая производная
функции либо равна нулю (![]() ),
либо не существует.
),
либо не существует.
Точки, в которых вторая производная функции равна нулю или не существует, называются критическими точками 2 –го рода. Точки перегиба следует искать среди критических точек 2- го рода.
Пусть функция имеет первую производную в точке и вторую производную в некоторой окрестности этой точки (кроме, быть может самой точки). Тогда, если при переходе через точку вторая производная меняет знак, то - точка перегиба.


Пример. Исследовать функцию на
интервалы выпуклости, вогнутости, найти
точки перегиба, если
![]() .
.
1.
![]() .
.
2. Решаем уравнение
![]() ,
т.е.
,
т.е.
![]() .
Получаем х=0.
.
Получаем х=0.
3. Определяем знак второй производной
в интервалах (-∞; 0) и (0; ∞). На интервале
(-∞; 0) знак второй производной отрицательный
![]() ,
график функции выпуклый. На интервале
(0; ∞)
,
график функции выпуклый. На интервале
(0; ∞)
![]() -
график функции вогнутый.
-
график функции вогнутый.
4.
![]() меняет знак в точке х=0, следовательно,
точка (0;5) – точка перегиба.
меняет знак в точке х=0, следовательно,
точка (0;5) – точка перегиба.
Наибольшее и наименьшее значения функции на отрезке.
Пусть функция
непрерывна на отрезке
![]() .
Функция достигает своего наибольшего
и наименьшего значения либо во внутренней
точке отрезка
.
Функция достигает своего наибольшего
и наименьшего значения либо во внутренней
точке отрезка
![]() ,
либо на границе х0=а
или х0=b.
Если
,
либо на границе х0=а
или х0=b.
Если
![]() ,
то х0 - критическая точка
данной функции.
,
то х0 - критическая точка
данной функции.
Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке:
Найти критические точки функции, т.е. решить уравнение .
Вычислить значение функции в тех критических точках, которые принадлежат интервалу
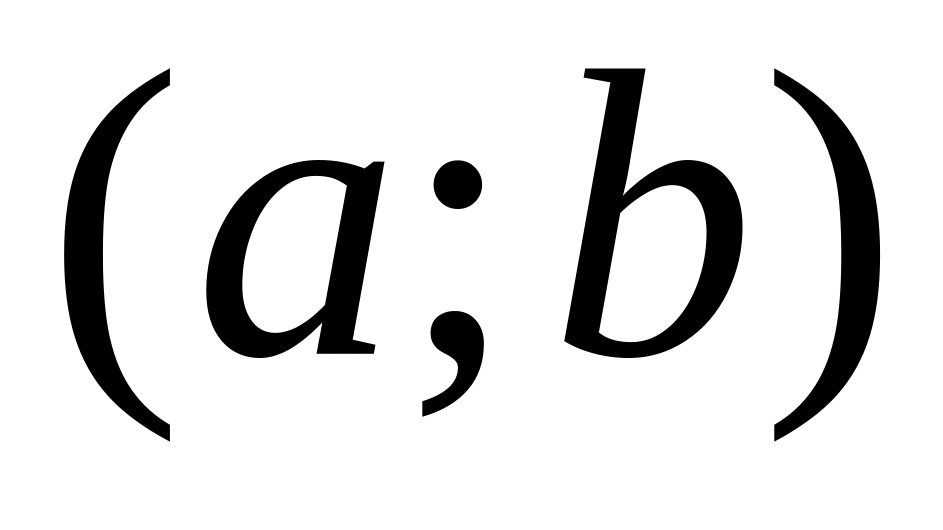 .
.Вычислить значение функции на концах отрезка в точках х=а и х=b.
Среди всех полученных значений функции выбрать наибольшее и наименьшее.
Если функция на отрезке не имеет критических точек, то это означает, что на нем функция монотонна убывает или возрастает. Следовательно, наибольшее и наименьшее значение принимает только на концах отрезка.
Пример. Найти наибольшее и наименьшее
значение функции
![]() на отрезке [-2;1].
на отрезке [-2;1].
1.
![]()
х1=0, х2=-1, обе точки принадлежат данному отрезку;
2. f(0)=1; f(-1)=3-4+1=0;
3. f(-2)=48-32+1=17; f(1)=3+4+1=8.
4. Наименьшее значение функции на отрезке [-2;1] f(-1)= 0,
наибольшее значение функции на отрезке [-2;1] f(-2)=17.
