
- •Драчева и.А. Математика
- •Часть 1
- •Методические указания
- •Содержание
- •Краткие сведения из теории и примеры решения задач.
- •Основные типы матриц:
- •Умножение матрицы на число. Все элементы исходной матрицы умножаются на заданное число. Например, .
- •Определители. Вычисление определителей.
- •Свойства определителей:
- •1Если некоторый столбец (или строка) состоит из нулей, то определитель равен 0.
- •Задания для самостоятельной работы
- •Практическое занятие № 2
- •2.1 Краткие сведения из теории и примеры решения задач.
- •5. Все элементы матрицы а* делим на величину определителя матрицы а.
- •Решение систем линейных алгебраических уравнений матричным методом
- •2.2 Задания для самостоятельной работы:
- •Практическое занятие № 3 Тема: Решение систем линейных алгебраических уравнений с помощью формул Крамера и методом Гаусса.
- •3.1 Краткие сведения из теории и примеры решения задач.
- •Решение систем линейных уравнений методом Гаусса.
- •3.2 Задания для самостоятельной работы.
- •Индивидуальная домашняя работа по теме «Системы линейных уравнений»
- •Практическое занятие № 4 Тема: Векторы. Действия над векторами, заданными проекциями.
- •Краткие сведения из теории и примеры решения задач.
- •Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
- •Задания для самостоятельной работы.
- •Практическое занятие № 5
- •5.1 Краткие сведения из теории и примеры решения задач.
- •5.2 Задания для самостоятельной работы.
- •6.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •7.1 Краткие сведения из теории и примеры решения задач.
- •7.2 Задания для самостоятельной работы.
- •8.1 Краткие сведения из теории и примеры решения задач.
- •8.2 Задания для самостоятельной работы.
- •10.1 Краткие сведения из теории и примеры решения задач.
- •10.2 Задания для самостоятельной работы.
- •11.1 Краткие сведения из теории и примеры решения задач.
- •11.2 Задания для самостоятельной работы.
- •12.1 Краткие сведения из теории и примеры решения задач.
- •12.2 Задания для самостоятельной работы.
- •13.1 Краткие сведения из теории и примеры решения задач.
- •13.2 Задания для самостоятельной работы
- •14.1 Краткие сведения из теории и примеры решения задач.
- •14.2 Задания для самостоятельной работы
- •15.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •16.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •17.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •18.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •Краткие сведения из теории и примеры решения задач.
- •19.2 Задания для самостоятельной работы
- •21.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •98309, Г. Керчь, Орджоникидзе, 82
14.2 Задания для самостоятельной работы
Найти производные сложных функций.
 9.
9.

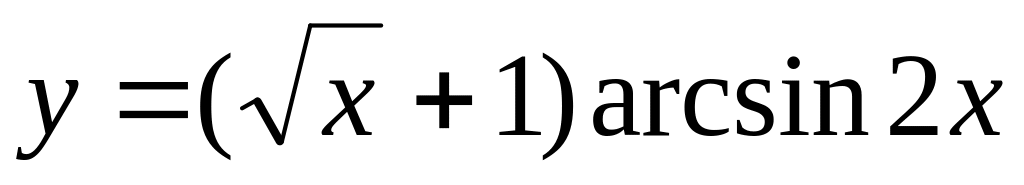 10.
10.

 11.
11.

 12.
12.

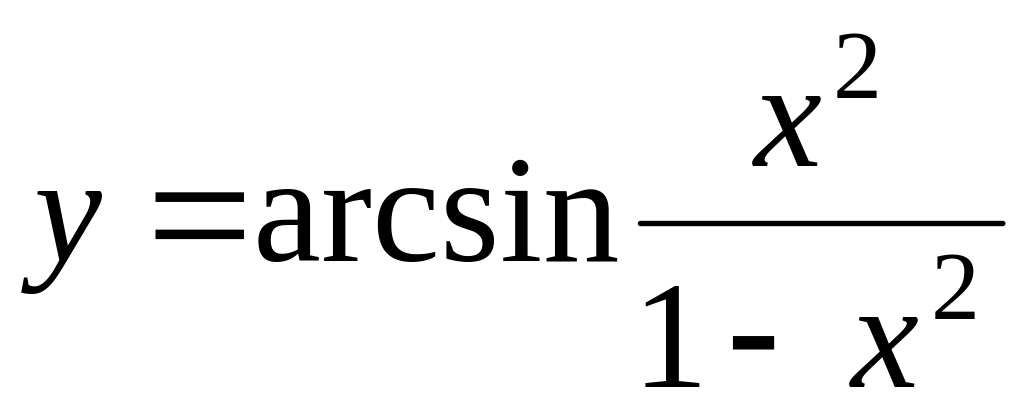 13.
13.

 14.
14.

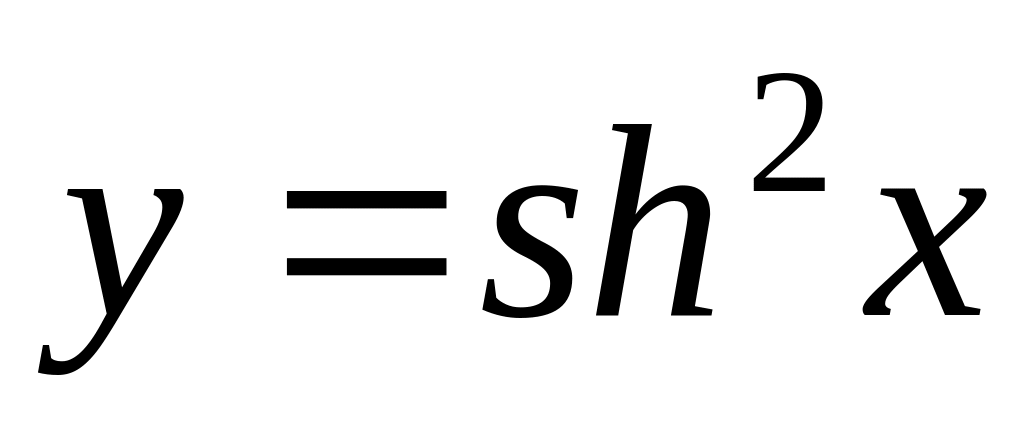 15.
15.

 16.
16.

11. № 751 – 759, № 786, № 858, № 864 [1]
Найти производные логарифмическим дифференцированием.
 4.
4.

 5.
5.

 6.
6.

Рекомендуемая литература: [2] стр. 81, [7] стр. 169, 181, [4] стр. 205-209.
ПРАКТИЧЕКСОЕ ЗАНЯТИЕ № 15
Тема: Нахождение производных неявных и параметрически заданных функций. Производные высших порядков.
15.1 Краткие сведения из теории и примеры решения задач.
Производная неявной функции.
Если функция задана уравнением , разрешенным относительно у, то говорят, что функция задана в явном виде (явная функция).
Функция, заданная в виде уравнения
![]() ,
не разрешенного относительно у,
называется неявно заданной.
,
не разрешенного относительно у,
называется неявно заданной.
Например:
![]() ,
,
![]() .
.
Если неявная функция задана уравнением
,
то для нахождения производной от у
по х нет необходимости разрешать
уравнение относительно у. Достаточно
продифференцировать это уравнение по
х, рассматривая при этом у как
функцию от х (![]() ),
и полученное затем уравнение разрешить
относительно
),
и полученное затем уравнение разрешить
относительно
![]() .
Производная неявной функции выражается
через аргумент х и функцию у.
.
Производная неявной функции выражается
через аргумент х и функцию у.
Пример:
![]() .
Найти
.
Найти
![]() .
.
![]()
Дифференцирование функции, заданной параметрически.
Иногда зависимость функции у от
аргумента х задается через посредство
третьей переменной, так называемого
параметра. А именно, зависимость между
аргументом х и функцией у задается
в виде двух уравнений:
![]() ,
где t – вспомогательная
переменная, называемая параметром.
Такой способ задания называется
параметрическим.
,
где t – вспомогательная
переменная, называемая параметром.
Такой способ задания называется
параметрическим.
Производная
![]() функции заданной параметрически
находится по формуле
функции заданной параметрически
находится по формуле
![]() .
.
Пример:
![]() .
Найти
.
.
Найти
.
Решение:
![]() ,
,

Производные высших порядков.
Производная
![]() функции
функции
![]() так же является функцией и называется
производной первого порядка.
так же является функцией и называется
производной первого порядка.
Если функция
![]() дифференцируема, то ее производная
называется производной второго порядка
и обозначается
дифференцируема, то ее производная
называется производной второго порядка
и обозначается
![]() (или
(или
![]() ).
).
Таким образом,
![]() .
.
Производная от производной второго
порядка, если она существует, называется
производной третьего порядка и
обозначается
![]() .
.
![]() ,
,![]() …
…
Производной n–го
порядка (или n–й
производной) называется производная
от производной порядка (n-1):
![]() .
.
Производные порядка выше первого называются производными высших порядков.
Пример 1.
![]() ,
найти производную третьего порядка.
,
найти производную третьего порядка.
![]() ;
;
![]() ;
;
![]() .
.
Пример 2. Найти
![]() ,
если
,
если
![]() .
.
Дифференцируем уравнение по х:
![]() .Отсюда
находим
.Отсюда
находим
![]() .
Далее
.
Далее
![]() .
.
Пример 3. Найти вторую производную,
если
![]() .
.
Функция задана параметрическими
уравнениями. Вторую производную находим
по формуле
 .
.
Решение: Находим первую производную
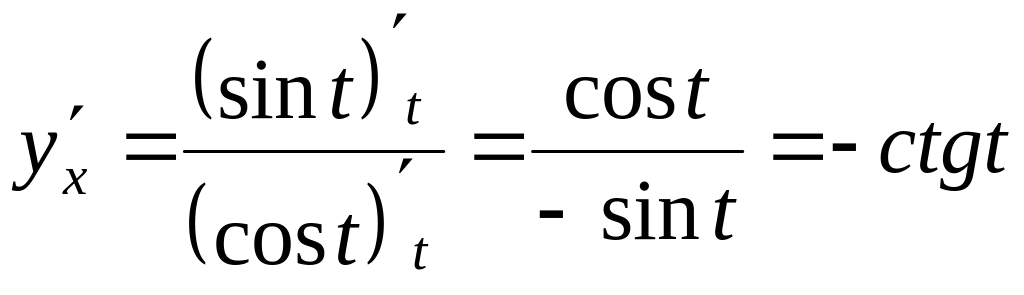 .
.
Находим вторую производную
 .
.
