
- •Драчева и.А. Математика
- •Часть 1
- •Методические указания
- •Содержание
- •Краткие сведения из теории и примеры решения задач.
- •Основные типы матриц:
- •Умножение матрицы на число. Все элементы исходной матрицы умножаются на заданное число. Например, .
- •Определители. Вычисление определителей.
- •Свойства определителей:
- •1Если некоторый столбец (или строка) состоит из нулей, то определитель равен 0.
- •Задания для самостоятельной работы
- •Практическое занятие № 2
- •2.1 Краткие сведения из теории и примеры решения задач.
- •5. Все элементы матрицы а* делим на величину определителя матрицы а.
- •Решение систем линейных алгебраических уравнений матричным методом
- •2.2 Задания для самостоятельной работы:
- •Практическое занятие № 3 Тема: Решение систем линейных алгебраических уравнений с помощью формул Крамера и методом Гаусса.
- •3.1 Краткие сведения из теории и примеры решения задач.
- •Решение систем линейных уравнений методом Гаусса.
- •3.2 Задания для самостоятельной работы.
- •Индивидуальная домашняя работа по теме «Системы линейных уравнений»
- •Практическое занятие № 4 Тема: Векторы. Действия над векторами, заданными проекциями.
- •Краткие сведения из теории и примеры решения задач.
- •Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
- •Задания для самостоятельной работы.
- •Практическое занятие № 5
- •5.1 Краткие сведения из теории и примеры решения задач.
- •5.2 Задания для самостоятельной работы.
- •6.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •7.1 Краткие сведения из теории и примеры решения задач.
- •7.2 Задания для самостоятельной работы.
- •8.1 Краткие сведения из теории и примеры решения задач.
- •8.2 Задания для самостоятельной работы.
- •10.1 Краткие сведения из теории и примеры решения задач.
- •10.2 Задания для самостоятельной работы.
- •11.1 Краткие сведения из теории и примеры решения задач.
- •11.2 Задания для самостоятельной работы.
- •12.1 Краткие сведения из теории и примеры решения задач.
- •12.2 Задания для самостоятельной работы.
- •13.1 Краткие сведения из теории и примеры решения задач.
- •13.2 Задания для самостоятельной работы
- •14.1 Краткие сведения из теории и примеры решения задач.
- •14.2 Задания для самостоятельной работы
- •15.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •16.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •17.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •18.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •Краткие сведения из теории и примеры решения задач.
- •19.2 Задания для самостоятельной работы
- •21.1 Краткие сведения из теории и примеры решения задач.
- •Задания для самостоятельной работы.
- •98309, Г. Керчь, Орджоникидзе, 82
13.1 Краткие сведения из теории и примеры решения задач.
Правила дифференцирования:
1.
![]()
2.
![]() ;
;
![]() с-const
с-const
3.
![]() ;
;
![]() с-const
с-const
4.
![]() ,
если
,
если
![]() ,
т.е.
,
т.е.
![]()
5.
![]() ,
если
и
,
если
и
![]() - взаимно обратные функции.
- взаимно обратные функции.
Формулы дифференцирования.
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
Примеры:
Пользуясь правилами и формулами дифференцирования, найти производные следующих функций:
1)
![]()
Перейдем к дробным показателям степени (выражения, содержащие корни) и к отрицательным показателям степени, получим выражение
![]()
![]()
2)
![]() .
.
Воспользуемся формулой производной
произведения
![]()
![]()
3)
![]() Воспользуемся формулой производной
частного
Воспользуемся формулой производной
частного
![]()

13.2 Задания для самостоятельной работы
Найти производные
 6.
6.

 7.
7.
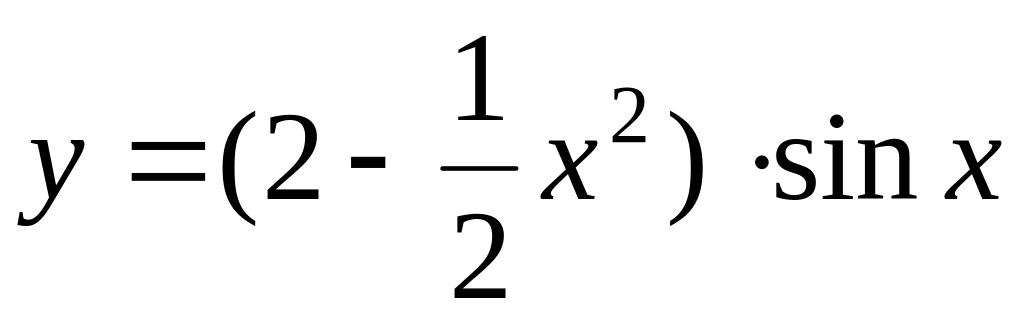
 8.
8.

 9.
9.

 10.
10.
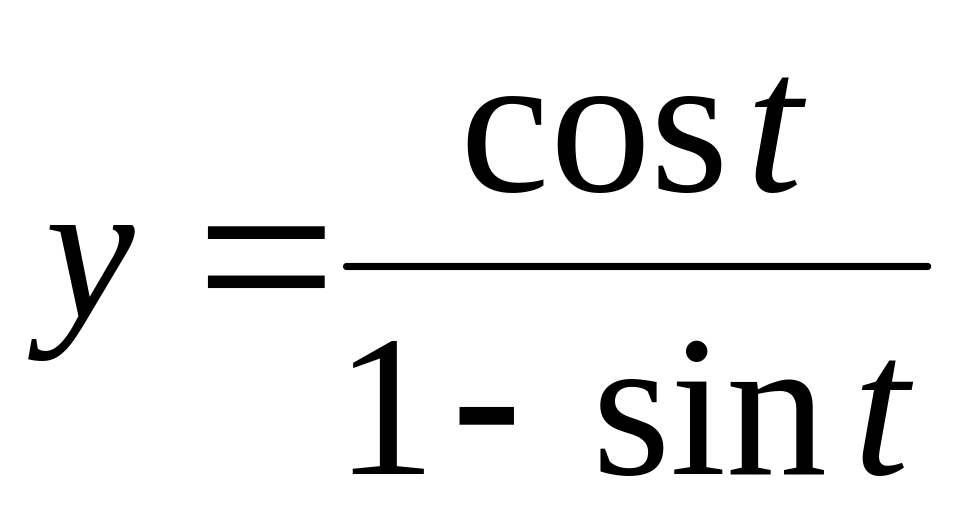
11. № 745-750, № 771-777 [1]
12. № 778 -780, № 782,№ 783 [1]
Рекомендуемая литература: [2] стр. 68-96, [7] стр. 167-177, [4] стр. 186-201.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 14
Тема: Нахождение производных сложных функций. Логарифмическое дифференцирование.
14.1 Краткие сведения из теории и примеры решения задач.
Пусть
![]() и
и
![]() ,
тогда
сложная функция с промежуточным
аргументом
,
тогда
сложная функция с промежуточным
аргументом
![]() и
независимым аргументом
и
независимым аргументом
![]() .
.
Производная сложной функции находится
по формуле
![]() .
.
Чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от «внешней» функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от «внутренней» функции по независимой переменной.
Пример 1. Найти производную сложной
функции
![]() .
.
Представим функцию в виде цепочки
простых функций
![]() ,
где
,
где
![]() .
.
![]() .
.
Пример 2. Найти производную сложной
функции
![]() .
.
Представим функцию в виде цепочки
простых функций
![]()
![]() .
.
Пример 3. Найти производную функции
![]() .
.
Здесь
![]() .
.
![]() .
.
Логарифмическое дифференцирование.
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать, а затем результат продифференцировать. Такую операцию называют логарифмическим дифференцированием.
Пример:
![]() .
Найти производную.
.
Найти производную.
Прологарифмируем данное выражение.
![]()
Дифференцируем по х:

Существуют функции, производные которых
находят лишь логарифмическим
дифференцированием. К их числу относятся
так называемые степенно-показательные
функции
![]() ,
где
,
где
![]() и
и
![]() дифференцируемые функции.
дифференцируемые функции.
Пример: Найти производную функции
![]() .
.
Логарифмируем данную функцию:
![]()
Дифференцируем, получаем:

![]()

