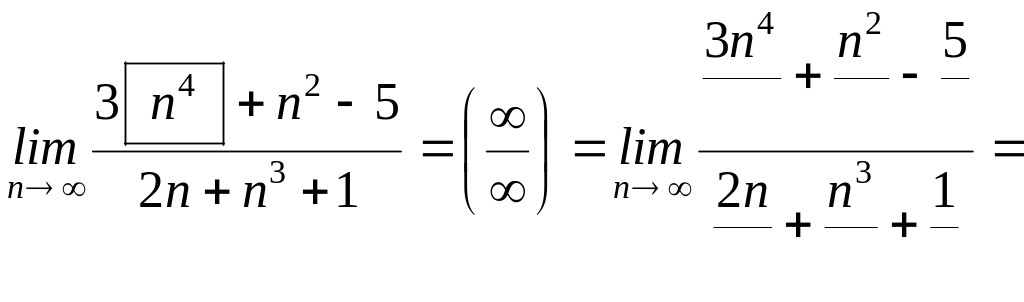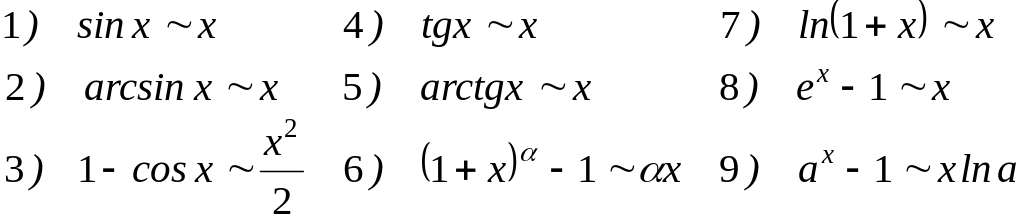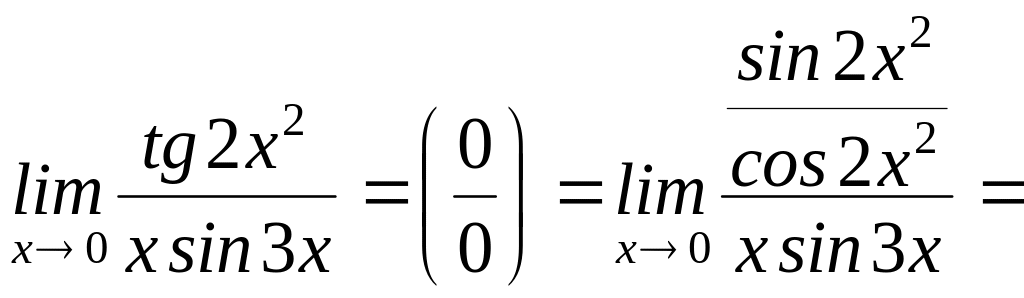Дана формула общего элемента последовательности. Указать пять первых её элементов:

Получили неопределённость типа , для её устранения разделим и числитель, и знаменатель дроби на старшую её степень, то есть на n⁵, а затем сократим дробь и вычислим полученный предел:

Получили неопределённость типа , для её устранения разделим и числитель, и знаменатель дроби на старшую её степень, то есть на ____, а затем сократим дробь и вычислим полученный предел:

Получили неопределённость типа , для её устранения разделим и числитель, и знаменатель дроби на старшую её степень, то есть на ____, а затем сократим дробь и вычислим полученный предел:

При вычислении предела последовательности в случае раскрытия неопределённости типа , можно руководствоваться следующим правилом:

Определяем старшую степень выражения и если «старшая степень находится»:

• в числителе, то предел равен бесконечности;

• в знаменателе, то предел равен нулю;

• и в числителе, и в знаменателе, то предел равен отношению коэффициентов при старших степенях.

3. Вычислить предел последовательности:

Первый замечательный предел (⁰/₀):

Эквивалентные

бесконечно малые функции.

при х0:

Второй замечательный предел (1^):

не противоречит основному правилу: «на нуль делить нельзя»

Получили неопределённость типа , для её устранения разложим и числитель, и знаменатель дроби на множители, затем сократим дробь и вычислим полученный предел:

х²-1=х²-1²=(х-1)(х+1);

х²+3х-4=0 (а=1; b=3; с=-4);

D=b²-4ac=3²-4·1·(-4)=9+16=25

х²+3х-4=1·(х-(-4))(х-1)=(х+4)(х-1).

при решении этого примера использовали:

• ФСУ – разность квадратов: а²-b²=(а-b)(а+b);

• разложение квадратного трёхчлена на множители: ах²+bх+с=а(х-х₁)(х-х₂), где х₁; х₂ – его корни.

Получили неопределённость типа , для её устранения разложим и числитель, и знаменатель дроби на множители, затем сократим дробь и вычислим полученный предел:

Получили неопределённость типа , для её устранения разложим знаменатель дроби на множители, умножим и числитель, и знаменатель дроби на выражение сопряжённое числителю, затем преобразуем, сократим дробь и вычислим полученный предел:

Получили неопределённость типа , для её устранения умножим и числитель, и знаменатель дроби на произведение выражений сопряжённых числителю и знаменателю, затем преобразуем, сократим дробь и вычислим полученный предел:

Получили неопределённость типа , для её устранения подведём пример к первому замечательному пределу:

Получили неопределённость типа , для её устранения подведём пример к первому замечательному пределу: