Вариант 11
№1. z1 = i, z2 = 8 + 8i
№2. z1 = 3 + i, z2 = 4 5i
№3.
z1
=
+ 2i,
z2
=
1 +
i
№4.
№5.
а)
sh(3
+
i);
б)
Arth
;
в)
№6.
а)
z
+ i
< 2, 0 < Rez
< 1, Imz
≤
1; б)
1 <
< 2, Rez
>
0, 0 ≤ Imz
≤ 1
№7. z = 3ch2t + i2sh2t
№8. w = z3 + 2z, z0 = 1 i
№9. v = 2xy + y, f(0) = 0
№10.
№11.
№12.
sin
,
z0
=
№13.
№14.
а)
;
б)
;
в)
;
г)
Вариант 12
№1. z1 = 2 + 2i, z2 = 3 i
№2. z1 = i, z2 = + i
№3. z1 = 3 + 3i, z2 = 2 2i
№4.
№5.
а)
sin(
5i);
б)
Arctg
;
в)
№6.
а)
z
1
i
< 1,
argz
≤
;
б)
№7. z = 2ch3t i3sh3t
№8. w = 3z2 2z, z0 = i
№9. v =3x2y y3 y, f(0) = 0
№10.
;
L:
z
= 4; Rez
0
№11.
№12.
sin
,
z0
= 2i
№13.
№14.
а)
;
б)
;
в)
;
г)
Вариант 13
№1. z1 = 2 i, z2 = 5 + 5i
№2. z1 = 2,5 i, z2 = 2 + 4i
№3.
z1
=
2
2
i,
z2
=
1
i
№4.
№5.
а)
cos(
2i);
б)
Arcth
;
в)
№6.
а)
z
1
> 1, 0 < Rez
< 3,
1 ≤ Imz
< 0; б)
№7. z = 5sh4t + i4ch4t
№8.
w
=
,
z0
= 3i
№9. u = x2 y2 2x +1, f(0) = 1
№10.
,
АВС – ломаная,
zА
= i,
zВ
= 1, zС
= 0
№11.
№12.
sin
,
z0
= i
№13.
№14.
а)
;
б)
;
в)
;
г)
Вариант 14
№1. z1 = 2 2 i, z2 = 2 + i
№2. z1 = 1 3i, z2 = 4 2i
№3. z1 = 1 i, z2 = 1 + i
№4.
№5.
а)
ln(
1 + i);
б)
Arctg
;
в)
№6.
а)
z
> 1, 0 < Rez
≤ 2,
1 < Imz
≤ 1; б)
Im
№7. z = 4sh5t i5ch5t
№8. w = 3z2 + 6z, z0 = 1 2i
№9. v = x2 y2 + 2x + 1, f(0) = i
№10.
;
АВ:
y
= x2
;
zА
= 0; zВ
=
1 + i
№11.
№12.
zsin
,
z0
= 1
№13. tg2z
№14.
а)
;
б)
;
в)
;
г)
Вариант 15
№1. z1 = i, z2 = 2 + 2i
№2. z1 = 4 + i, z2 = 1 i
№3. z1 = 1 i, z2 = + i
№4.
№5. а) Ln(1 + i); б) Arch3i; в) ctgi
№6. а) z < 2, Rez 1, argz < ; б) z > 2+Imz
№7.
z
=
+ i2th2t
№8.
w
= 3z2
+ 4z,
z0
=
1 +
i
№9. u = y 2xy, f(0) = 0
№10.
;
АВ:
z
= 1, Imz
0,
ВС– отрезок,
zВ
= 1, zС
= 2
№11.
№12.
z
,
z0
= 5
№13.
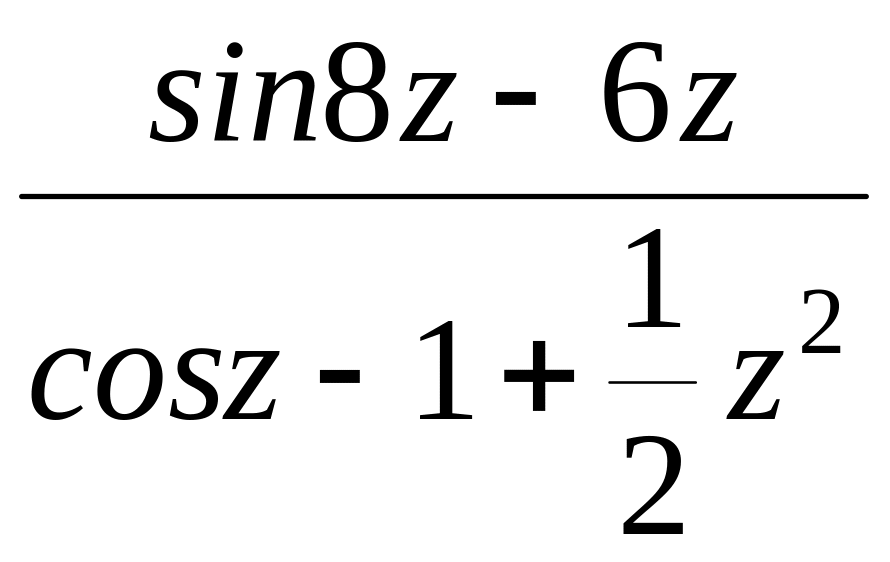
№14.
а)
;
б)
;
в)
;
г)
Вариант 16
№1.
z1
=
,
z2
=
3i
№2. z1 = + 3i, z2 = 4 i
№3. z1 = 7 + 7 i, z2 = 1 i
№4.
№5.
а)
ch(1
i);
б)
Ln
;
в)
№6.
а)
z
< 2,
;
б)
1 ≤
z
i
< 2
Rez
≤ 0, Imz
> 1
№7.
z
=
+ i2tg4t
№8. w = 3z2 4z, z0 = 1 i
№9. u = eycosx, f(0) = 1
№10.
,
АВ – отрезок
прямой от zА
= 1 + i
до zВ
= 0
№11.
№12. sin , z0 =
№13. z2sin
№14.
а)
;
б)
;
в)
;
г)