Типовой расчет теория функций комплексного переменного

№1. Изобразить число на комплексной плоскости. Записать его в тригонометрической и показательной формах.

№2. Вычислить в алгебраической форме z₁  z₂; z₁ + z₂; ; z₁; z₁ .

№3. Записать числа в тригонометрической и показательной формах. Вычислить z₁  z₂.и в тригонометрической и показательной формах.

№4. Найти все значения корня и изобразить их на комплексной плоскости.

№5. Представить в алгебраической форме.

№6. Вычертить область, заданную неравенствами.

№7. Определить вид кривой.

№8. Определить коэффициент растяжения и угол поворота при отображении w в точке z₀.

№9. Восстановить аналитическую в окрестности точки z₀ функцию f(z) по известной действительной части u(x,y) или мнимой v(x,y) и значению f(z₀).

№10. Вычислить интеграл от функции комплексного переменного по данной кривой.

№11. Найти все лорановские разложения данной функции по степеням z.

№12. Данную функцию разложить в ряд Лорана в окрестности точки z₀.

№13. Найти изолированные особые точки и определить их тип.

№14. Вычислить интегралы (а – в) двумя способами: по интегральной формуле Коши и по теореме о вычетах. В случае (г) вычислить интеграл одним способом (любым).

Вариант 1

№1. z₁ = 1  i, z₂ = 5 + 5i

№2. z₁ =  2  3i, z₂ = 5  5i

№3. z₁ =  1 + i, z₂ = + i

№4.

№5. а) cos( i); б) Arcth ; в)

№6. а)  z  1 + i   1, Rez < 1, Imz ≤  1; б)  argz  ≤

№7. z = 3sect + i2tgt

№8. w = z³ + 6z, z₀ = 1  i

№9. u = , f(1) = 2

№10. , L – отрезок прямой от z₀ = 1 до z₁ = 1 + i

№11.

№12. z²sin , z₀ = 0

№13.

№14. а) ; б) ;

в) ; г)

Вариант 2

№1. z₁ = i, z₂ =  i

№2. z₁ = 4  6i, z₂ =  1 + i

№3. z₁ = 1  i, z₂ =  + i

№4.

№5. а) sin( 2i); б) i³ⁱ; в) Arth

№6. а) 0 ≤ Re( iz ) < 1; б)  z + i  < 2

№7. z = 2sect  i3tgt

№8. w = z²  2z, z₀ = 2  i

№9. u = , f(0) = 1

№10. ; АВ– отрезок прямой, z_А = 0, z_В = 1 + 2i

№11.

№12. cos , z₀ = 2

№13.

№14. а) ; б) ;

в) ; г)

Вариант 3

№1. z₁ =  1, z ₂ = 5  5i

№2. z₁ = 2  3i, z ₂ =  3 + 5i

№3. z₁ = 1  i, z ₂ =  6+ 6i

№4.

№5. а) 1²ⁱ; б) Arcctg ; в) ln(  2 + 5i)

№6. а)  z  1 + i   1, Rez < 1, Imz ≤  1; б)  argz  ≤

№7. z =  sect + i3tgt

№8. w = z² + 2z, z₀ =  2  i

№9. v = e^ysinx, f(0) = 1

№10. ; АВ – отрезок прямой, z_А = 0, z_В = 1 + 2i

№11.

№12. , z₀ = а

№13.

№14. а)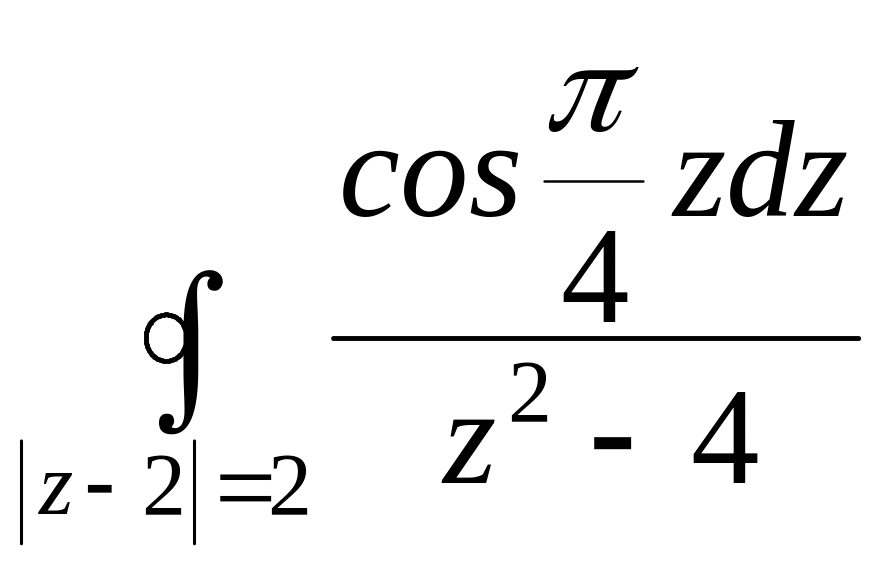 ; б) ;

в) ; г)

Вариант 4

№1. z₁ = 6  6i, z ₂ =   i

№2. z₁ = 4  3i, z ₂ =  7  i

№3. z₁ = 1  i, z ₂ = 2 + 2i

№4.

№5. а) ch( i); б) Arctg ; в)

№6. а)  z  i  ≤ 2, Rez > 1; б) 0 ≤ arg(z + i) < π

№7. z = 4tgt i3sect

№8. w = z²  2z, z₀ = 2 + i

№9. u = e^ycosx + x, f(0) = 1

№10. ; АВС – ломаная, z_А = 0, z_В =  1 + i, z_С = i

№11.

№12. zсos , z₀ = 2

№13.

№14. а) ; б) ;

в) ; г)