
Ключи к олимпиадным заданиям по физике
класс
Задача 1. В цепь, состоящую их медного провода, включают свинцовый предохранитель. Какое сечение должен иметь предохранитель, чтобы при нагревании провода более чем на t = 10оС он расплавился? Начальная температура свинца t = 27оС, температура плавления свинца t = 327оС.
Этапы решения |
Уравнение теплового баланса для проводов c1m1t1=
I2R1.
(1) (c1 –
удельная теплоемкость меди, m1
–масса проводов). Учитывая, что
m1=d1s1l1,
(d1 –
плотность меди, s1
и l1–
сечение и длина медного провода),
|
Уравнение теплового баланса для свинцового предохранителя c2m2t2+ m2= I2R2. (3) (c2– удельная теплоемкость свинца, m2–масса предохранителя, d2 – плотность свинца, s2 и l2– сечение и длина предохранителя, - удельная теплота плавления свинца). Подставляя
в (3) m2=d2s2l2,
и |
Поделив (4) на (2), после несложных преобразований и подстановки числовых значений, получим
|
|
Задача 2. Тело брошено со скоростью 10 м/с под углом 60◦ к горизонту. На какой высоте кинетическая энергия тела будет равна потенциальной? Ускорение свободного падения равно 10 м/с2. Начальную высоту (и потенциальную энергию на этой высоте) примите равной нулю.
Решение. Поскольку полная механическая энергия тела сохраняется, в момент, когда кинетическая и потенциальная энергии тела будут равны друг другу, они будут равны половине начальной кинетической энергии, то есть
mgh=
 ,
откуда h
=
,
откуда h
=
 =
2,5 м. Это меньше, чем максимальная высота
подъема тела, равная примерно 3,75 м при
условиях задачи, так что ответ правильный!
=
2,5 м. Это меньше, чем максимальная высота
подъема тела, равная примерно 3,75 м при
условиях задачи, так что ответ правильный!
Задача 3. В сосуде, содержащем 2 л воды при 0◦С, находится 500 г льда при нулевой температуре. Всосуд наливают еще 500 г воды при 100 ◦C. Определите, сколько льда растает и какова установившаяся температура. Теплоемкость воды 4200 Дж/(кг ◦С), удельная теплота плавления льда –– 335000 Дж/кг.
Решение. Пусть m1 –– масса исходной воды, m2 –– масса долитой воды, m0 –– масса льда, L––удельная теплота плавления льда, c –– теплоемкость воды, T =100 ◦C. Уравнение теплового баланса в случае, когда лед полностью растаял:
m0L+(m0
+m1)ct=
m2(T-t)c,
t=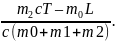 Это
число получается больше 0, поэтому
растает весь лед и установится ненулевая
температура t =3,4 градуса Цельсия.
Это
число получается больше 0, поэтому
растает весь лед и установится ненулевая
температура t =3,4 градуса Цельсия.
Задача 4.
Автобус за 30 минут проехал 30 км, следующие 45 минут он двигался со скоростью 70 км/ч. Определите среднюю скорость автобуса на всём пути.
Решение: Общее время движения 30 мин + 45 мин = 75 мин = 5/4 ч; путь, пройденный за 45 мин – 70 км/ч∙3/4 ч = 52,5 км. Общий путь 30 км + 52,5 км = 82,5 км. Vср = S/t = 82,5/(5/4) = 66 км/ч.
Задача 5
С помощью системы из подвижного и
неподвижного блоков поднимают с
поверхности земли груз массой m = 15 кг.
За какое время груз достигнет высоты Н
= 1,1 м, если верѐвку тянуть с постоянной
силой Q = 90 Н? Массами верѐвки, блоков и
трением в осях блоков пренебречь.
помощью системы из подвижного и
неподвижного блоков поднимают с
поверхности земли груз массой m = 15 кг.
За какое время груз достигнет высоты Н
= 1,1 м, если верѐвку тянуть с постоянной
силой Q = 90 Н? Массами верѐвки, блоков и
трением в осях блоков пренебречь.
Решение:


 (1-
удельное сопротивление меди), получим
(1-
удельное сопротивление меди), получим
 (2)
(2) ,
получим
,
получим
 (4).
(4). ;
s2
;
s2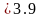 мм.
мм.