Взаимное расположение двух прямых
Пусть две прямые и заданы уравнениями
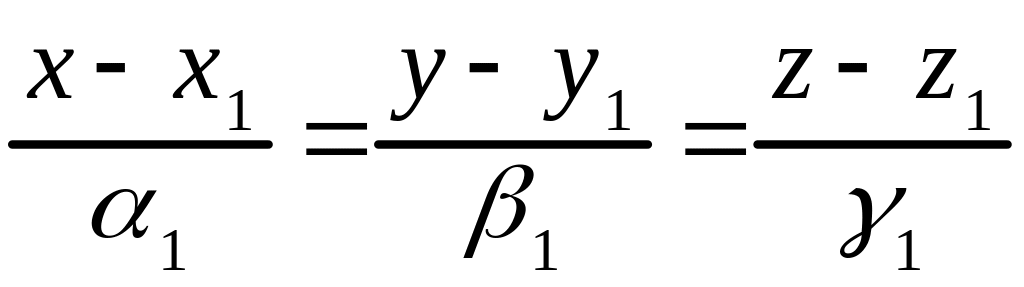и
,
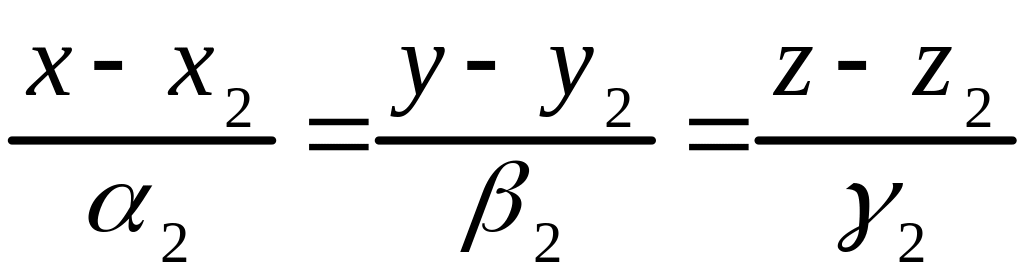соответственно.
Две
прямые в пространстве могут: а)
скрещиваться, б) пересекаться, в) быть
параллельными, г) совпадать. Определить,
как именно располагаются кривые, можно
при помощи направляющих векторов прямых
,
и вектора
.
А именно:
а) если
смешанное
произведение векторов
,
и
не равно 0, т.е., если
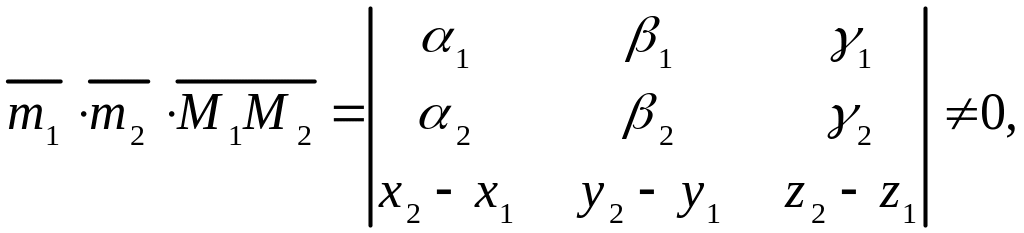(3.10)
то прямые и скрещиваются;
б) если
и выполняется одно из неравенств:
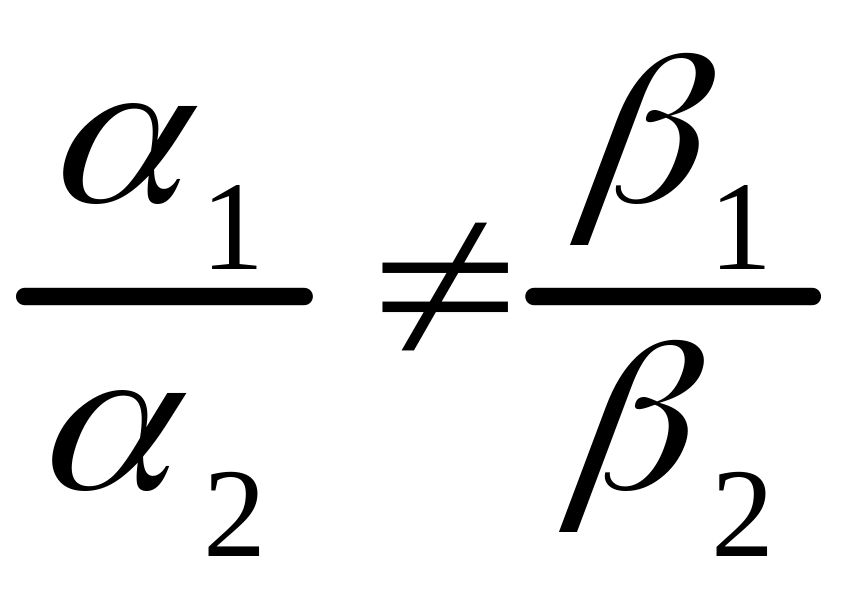или
,
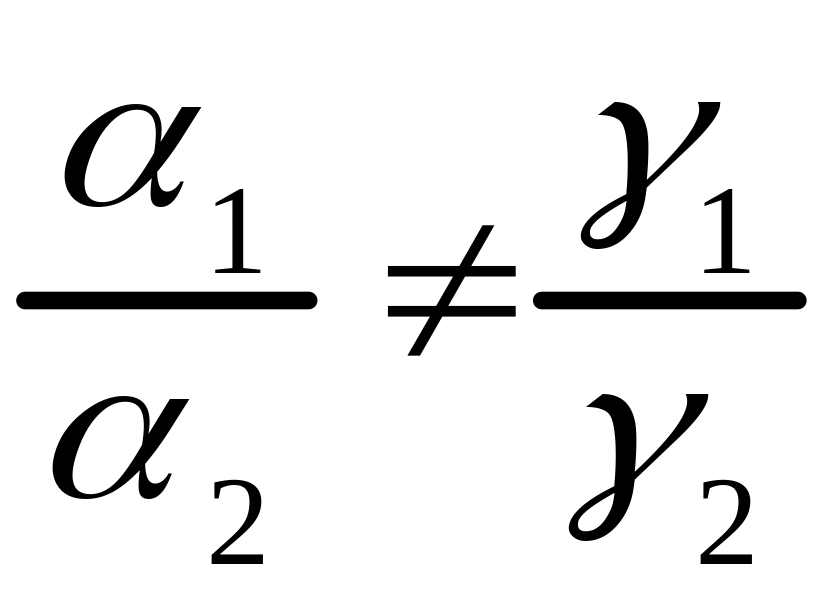т.е., если
,
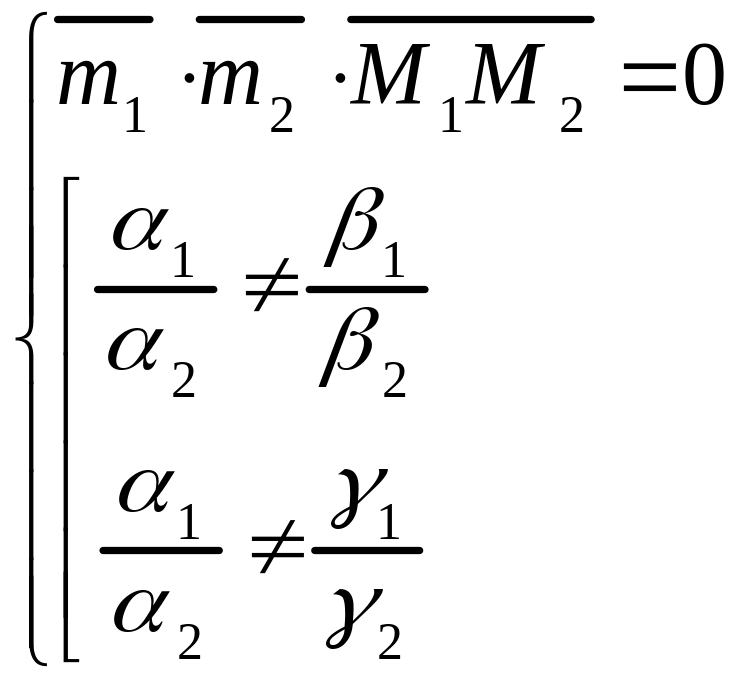(3.11)
то прямые и пересекаются;
в) если
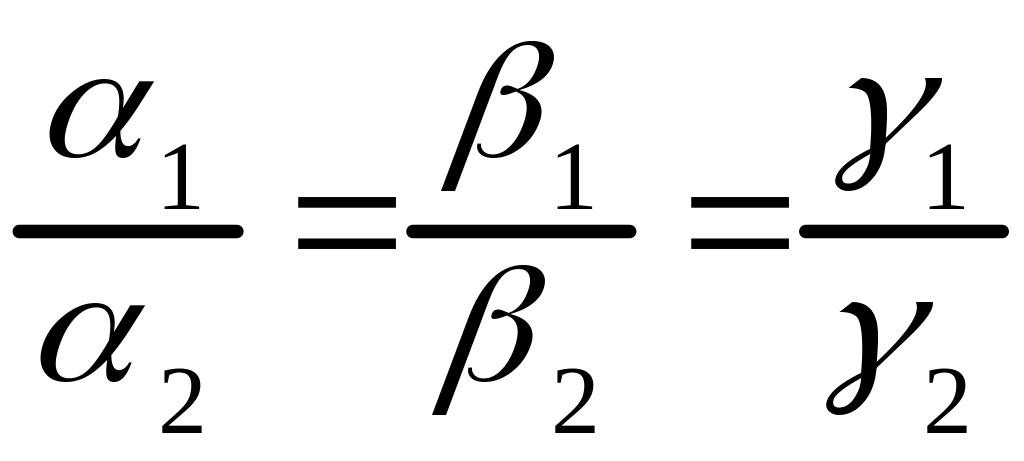и выполняется одно
из неравенств:
или
,
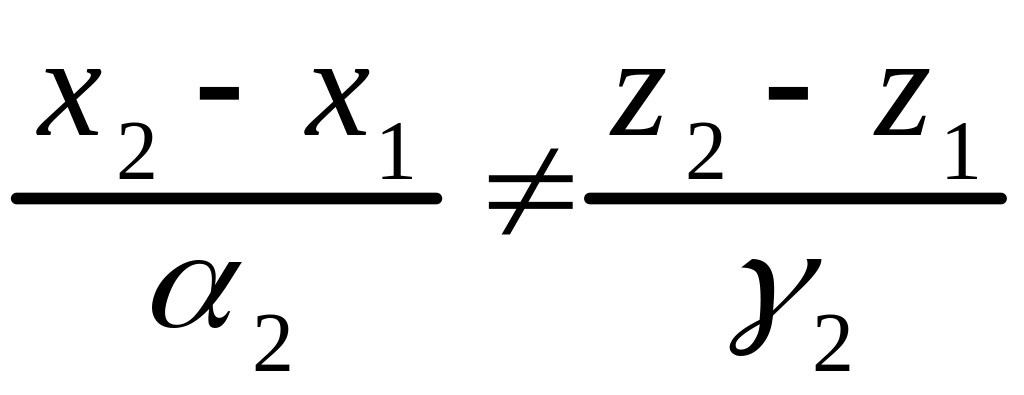т.е., если
,
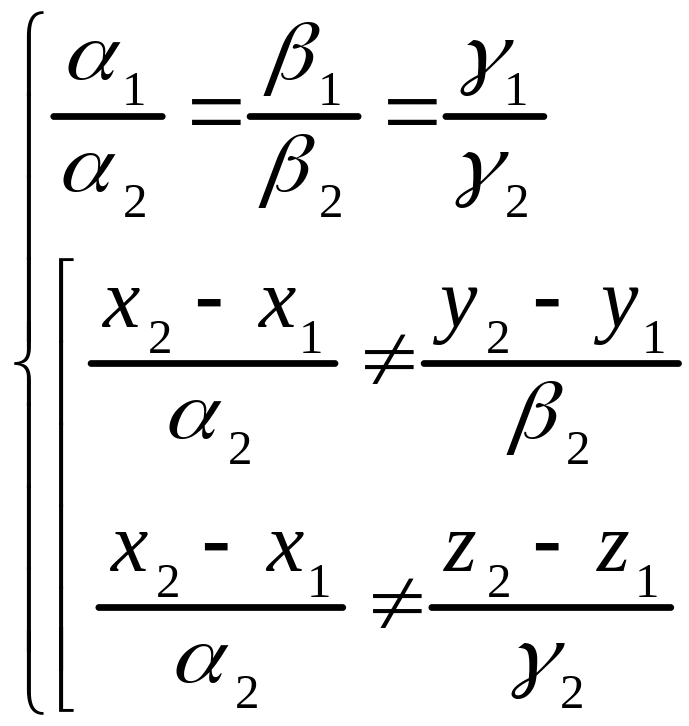(3.12)
то прямые и параллельны;
г) если
,
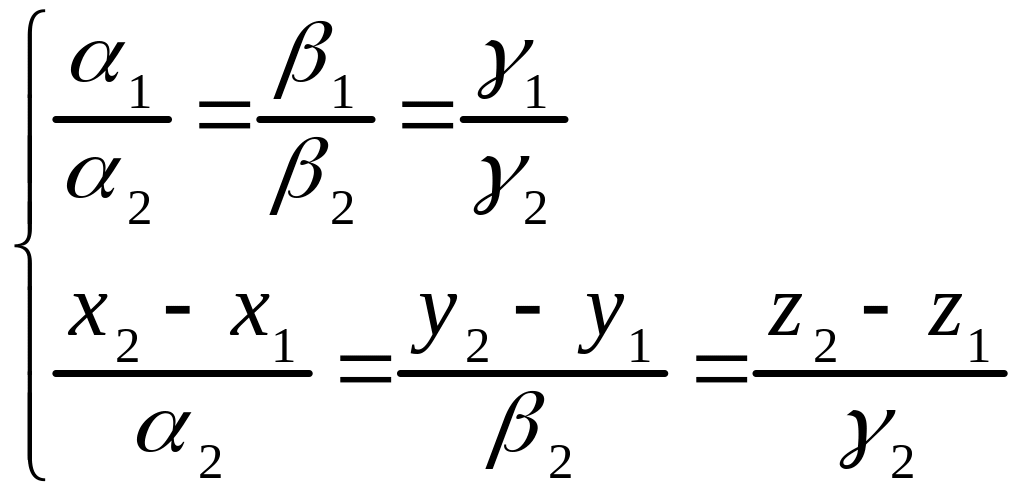(3.13)
то прямые и совпадают.
Точка
лежит на пересечении прямых
и
тогда
и только тогда, когда при подстановке
ее координат в каждое из уравнений
получаем верное равенство, т.е.
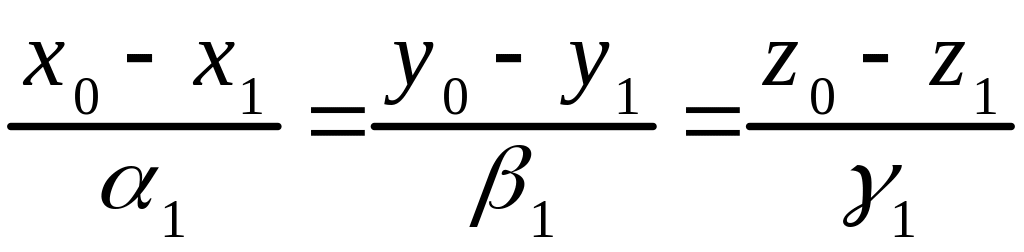и
.
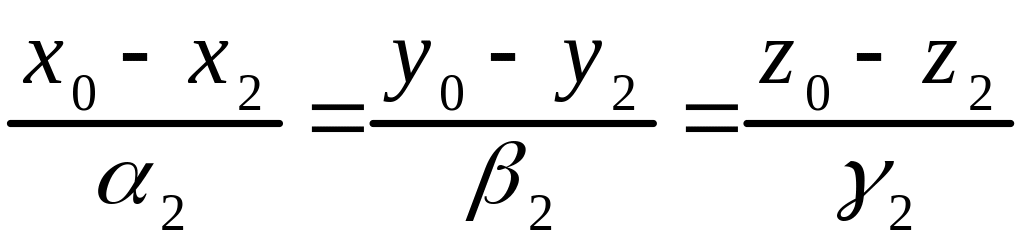Следовательно,
координаты точки
являются решением системы уравнений:
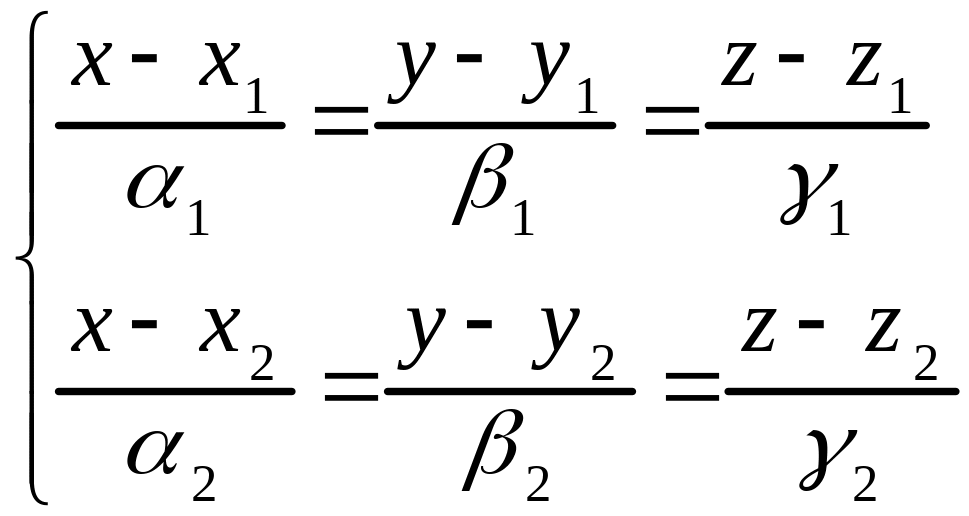(3.14)
или
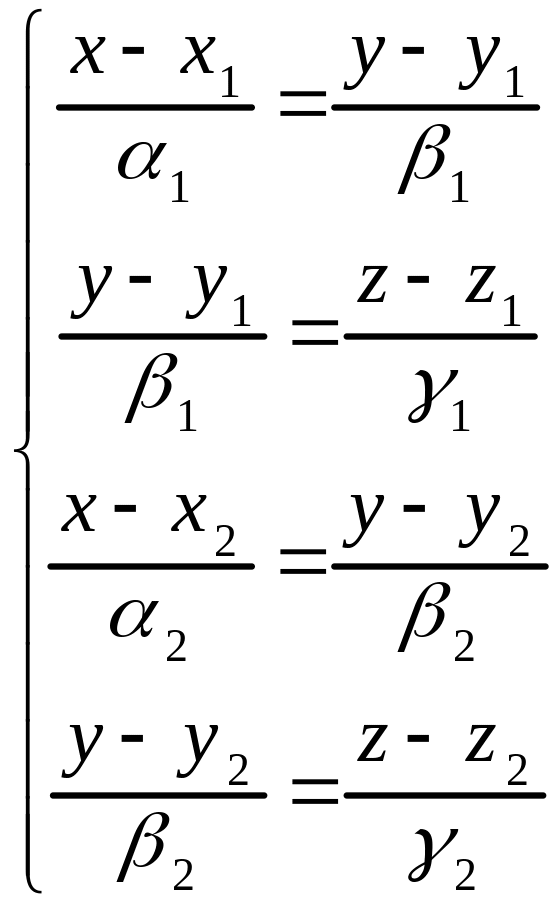(3.15)
Если система имеет 1 решение, то прямые пересекаются и решение системы уравнений – координаты точки пересечения.
Если система имеет бесконечно много решений, то прямые совпадают. Если система не имеет решений, то прямые параллельны или скрещиваются.
Угол между прямыми и равен углу между их направляющими векторами и , который находится из формулы
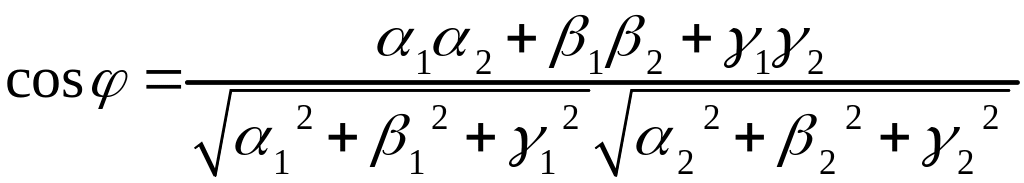(3.16)
Так как две прямые образуют два угла в сумме равных , то, если , найден косинус большего из них, а, в противном случае, – меньшего.
Две прямые перпендикулярны тогда и только тогда, когда косинус угла между ними равен 0. Следовательно, условие перпендикулярности прямых и имеет вид:
.
(3.17)
Расстояние от точки до прямой
Пусть прямая
задана уравнением
.
Расстояние
от точки
до прямой
равно длине перпендикуляра, опущенного
из точки
на
.
Пусть
,
а вектора
.
Тогда
вычисляется
по формуле
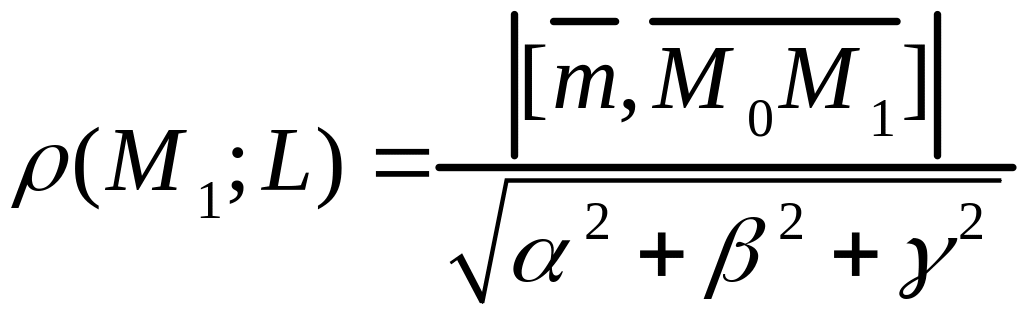(3.18)
Расстояние между двумя прямыми
Пусть прямая проходит через точку параллельно вектору , а прямая – через точку параллельно
В этом случае прямые и задаются уравнениями и
, соответственно.
Если
и
параллельны,
то расстояние
между
ними равно расстоянию
от точки
до
прямой
,
т.е.
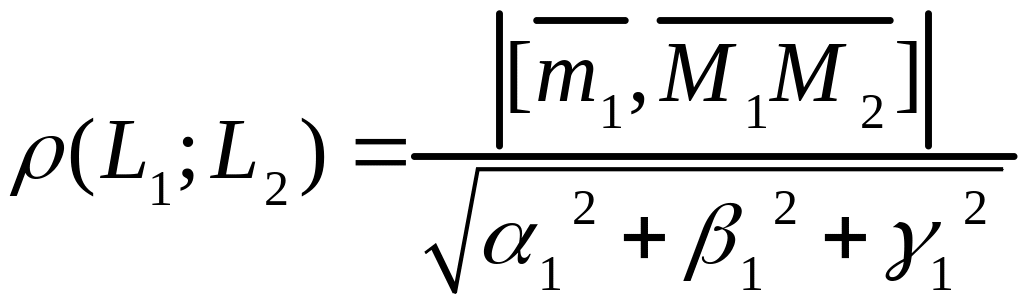(3.19)
Если и скрещиваются, то расстояние между ними равно расстоянию между параллельными плоскостями и , которые содержат прямые и , соответственно. Это расстояние находится по формуле
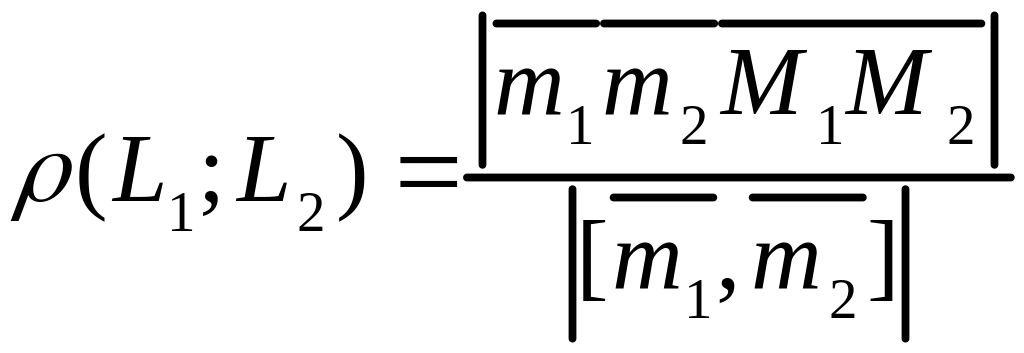(3.20)
Пример 23. Даны прямые и . Определить угол между ними, найти точку пересечения, если они пересекаются, и расстояние между ними в противном случае:
1)
;
;
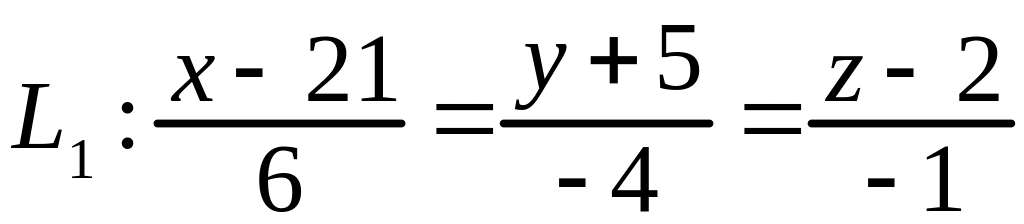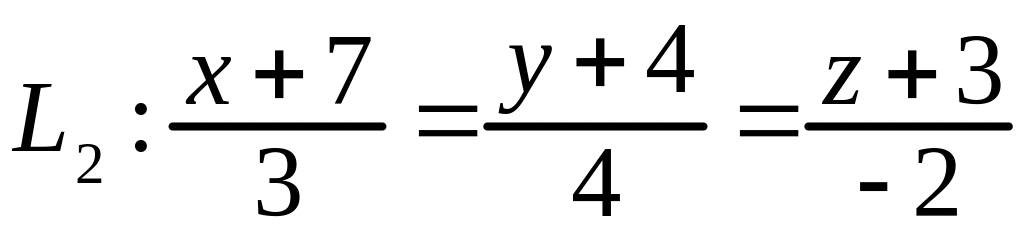2)
;
;
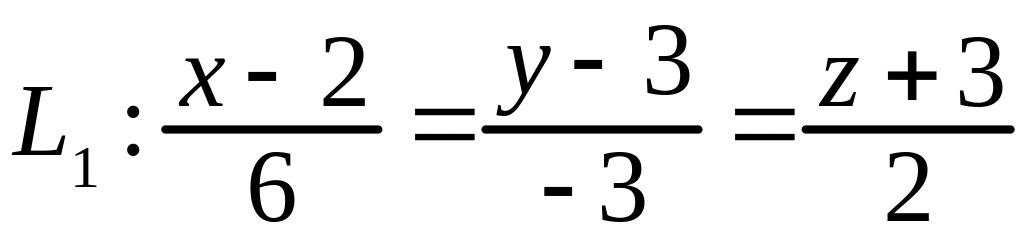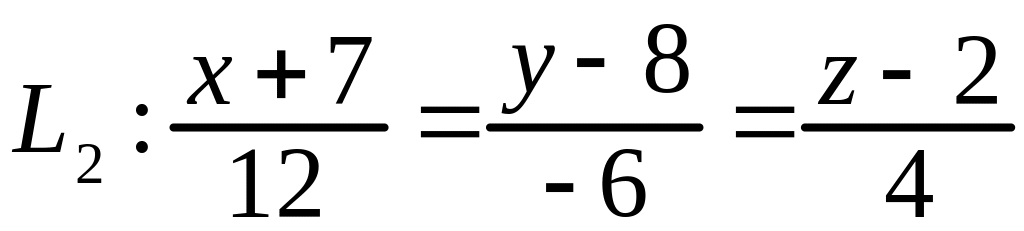3)
;
;
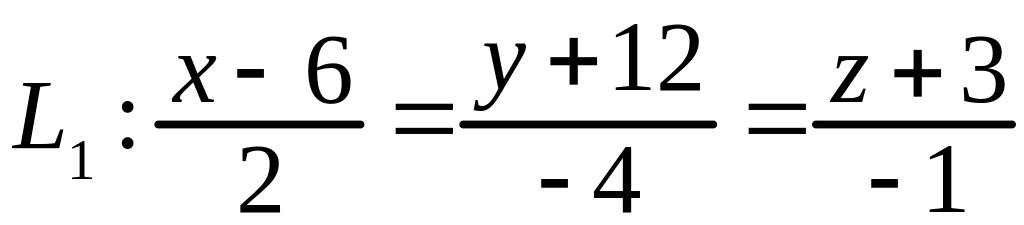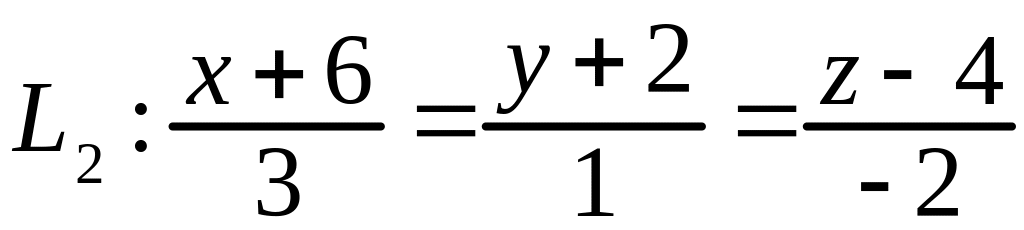Решение. Из канонических уравнений прямых и находим
их направляющие векторы и , точки и , лежащие на прямых, и вектор .
1) В
этом случае
,
,
,
,
.
Угол между прямыми находим из (3.16)
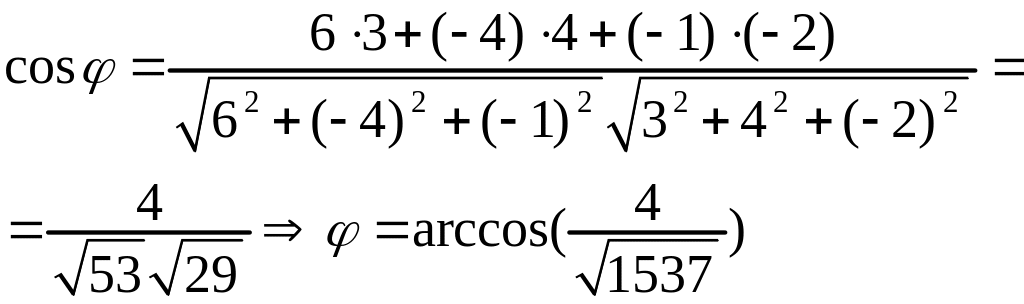
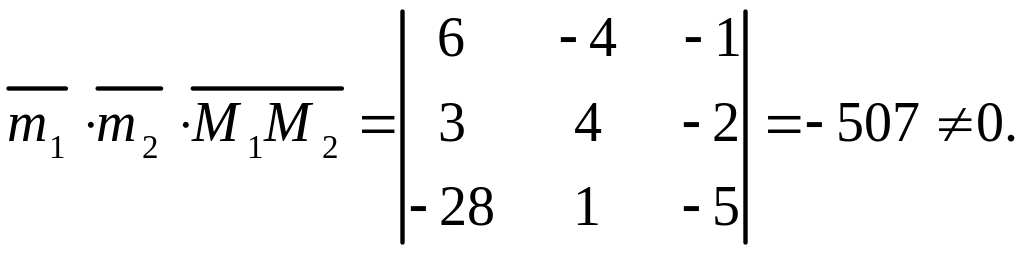
Из (3.10) следует, что и скрещиваются. Значит, точек
пересечения нет, а для нахождения расстояния между и
надо
(см. (3.20)) найти
.
.
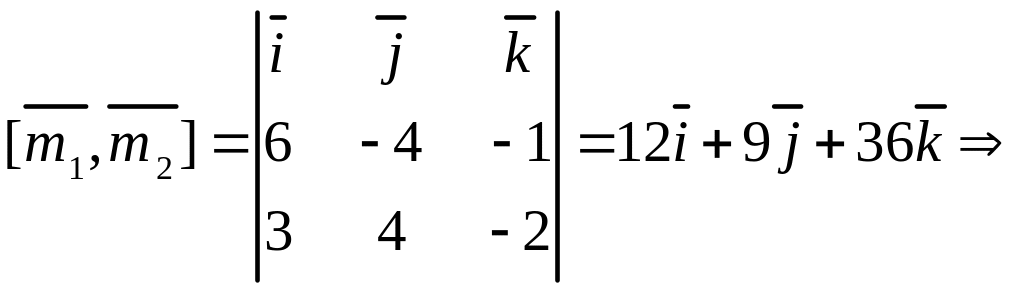
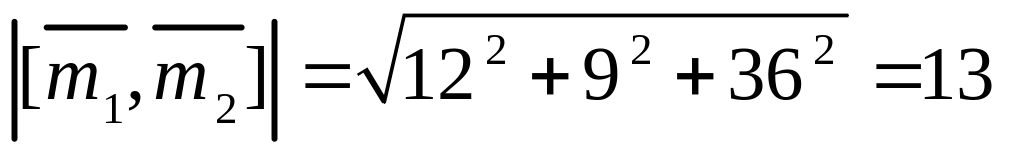Из (3.20)
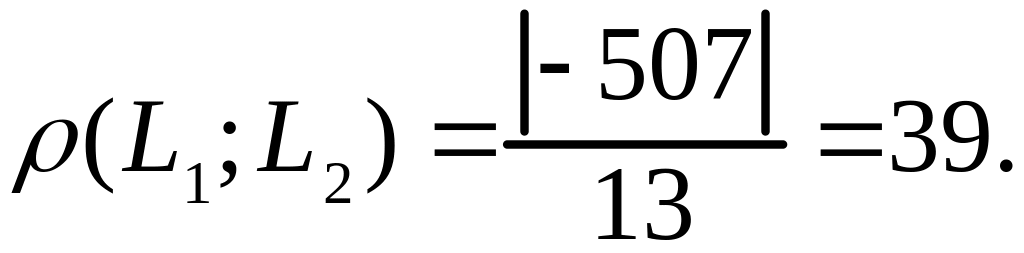
2) В
этом случае
,
,
,
,
.
.
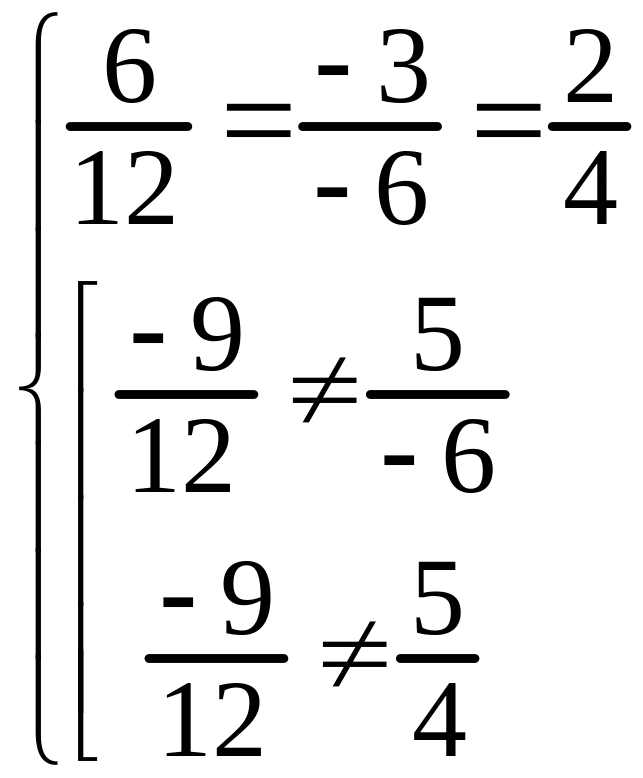Из (3.12) следует, что и параллельны. Значит, угол между ними равен 0. Расстояние между параллельными прямыми вычисляется по формуле (3.19).
Находим
.
.
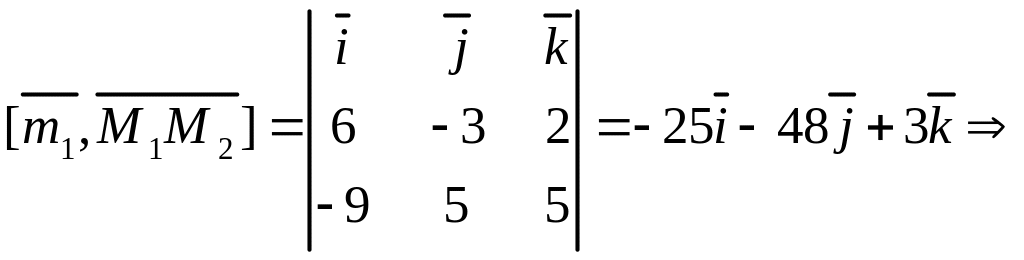
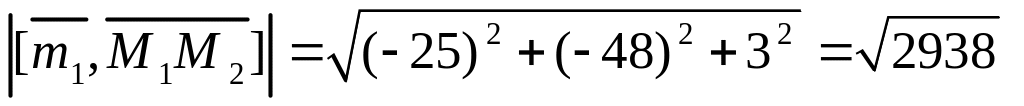Из (3.19) получаем
.
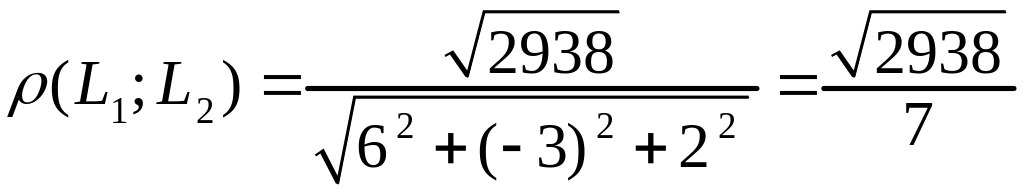3)
В этом случае
,
,
,
,
.
Угол между прямыми находим из (3.16)
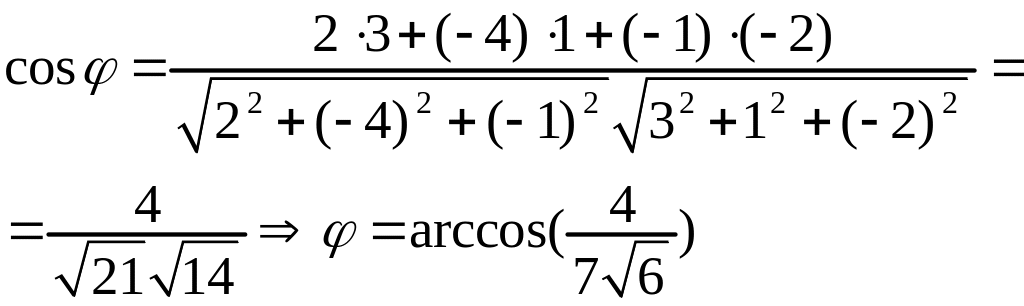
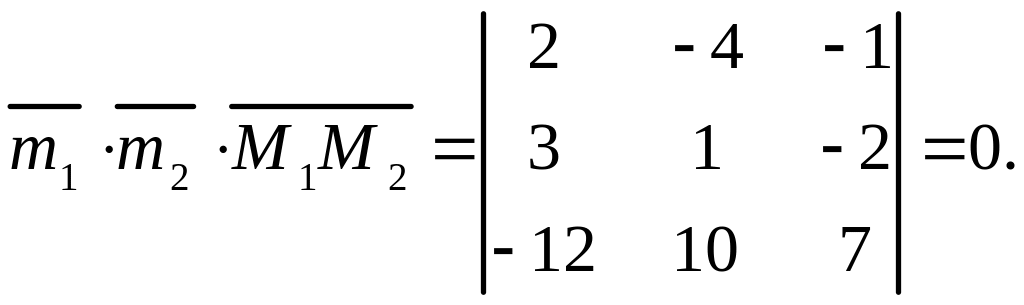
Из (3.11) следует, что и пересекаются. Координаты точки пересечения находим, решая систему уравнений (3.15):
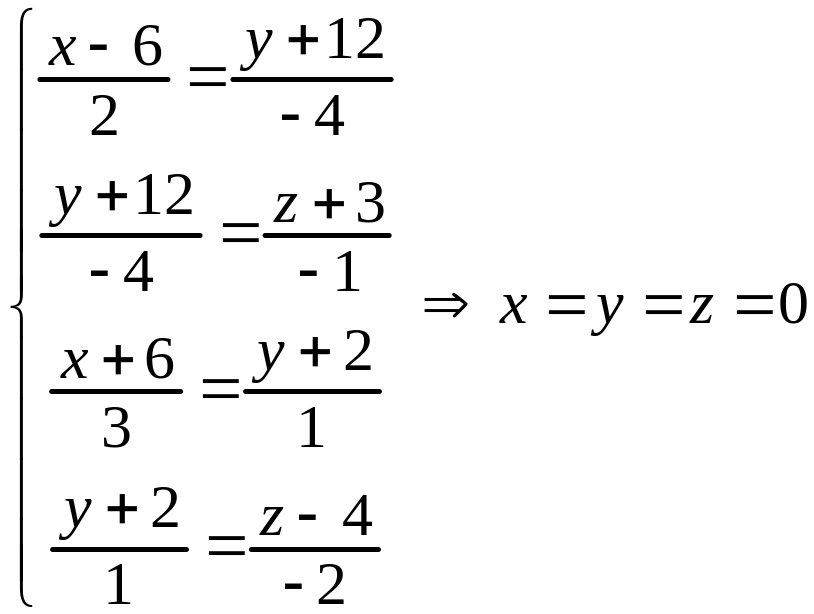Значит,
прямые пересекаются в точке