Задачи для самостоятельного решения
1. Составить уравнение прямой, отсекающей на осях координат отрезки a = 2/5, b= –1/10. Написать также: 1) уравнение с угловым коэффициентом; 2) общее уравнение; 3) нормальнее уравнение.
2. Дано общее уравнение прямой 12x–5у– 65=0. Написать:
1) уравнение с угловым коэффициентом; 2) уравнение в отрезках; 3) нормальнее уравнение.
3.Можно ли уравнение прямой 20x + 21 y = 0 записать в отрезках?
4. Составить уравнение прямой, проходящей через точку М(–2; 3) перпендикулярно прямой 4x–8y=0.
5. Прямая отсекает на осях координат равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного прямой с осями координат, равна 8 кв. ед.
6. Составить уравнение прямой, проходящей через начало координат и точку А(–2; –3).
7. Составить уравнение прямой, проходящей через точку А (2; 5) и отсекающей на оси ординат отрезок b = 7.
8.Составить уравнения прямых, проходящих через точку М (–3; –4) и параллельных осям координат.
9.Составить уравнение прямой, проходящей через точку М(–2; 3) параллельно прямой
.
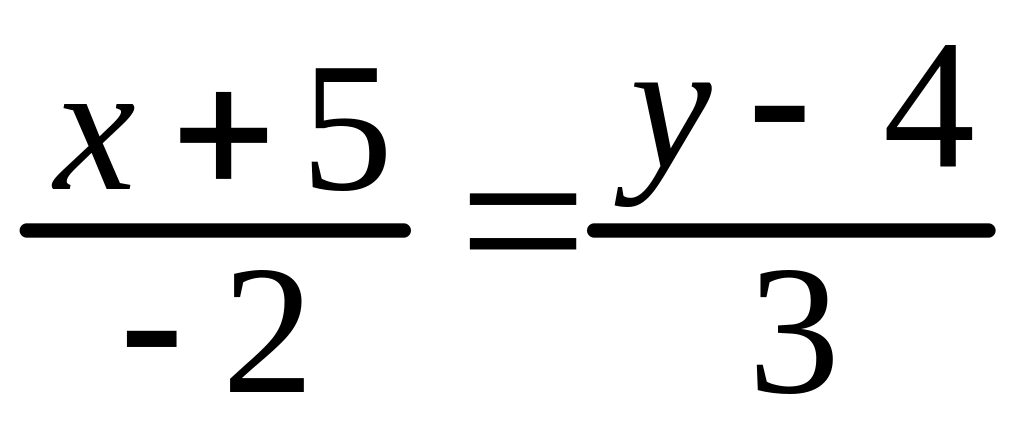10. Составить уравнение прямой, проходящей через точку М (–2; –5) и параллельной прямой Зх+4y + 2 = 0.
11. Определить острый угол между прямыми у =–Зx + 7 и прямой, проходящей через точки М(–3;–4) и N(2; – 4).
12. Показать, что прямые 2х–6y + 7 = 0 и 20x – 30y –11=0 параллельны. Найти расстояние между ними.
13. Показать, что прямые 3x–5y + 7 = 0 и 10x +6y –3 = 0 перпендикулярны.
14.Показать, что прямые 3x – 2у+1 = 0 и 2x+5y–12 = 0 пересекаются, и найти координаты точки пересечения и угол между прямыми.
15.
Составить уравнение прямой, проходящей
через точку пересечения прямых
и 3x+4y–1=0
параллельно прямой
.
16. Найти прямую, проходящую через точку пересечения прямых 5х+3у + 10 = 0, х + у – 15 = 0 и через начало координат.
17. Показать, что прямые 3x – 2у+1 = 0 и 2x+5y–12 = 0 пересекаются, и найти координаты точки пересечения и угол между прямыми.
18.
Определить расстояние от точки М(–3;3)
до
прямой
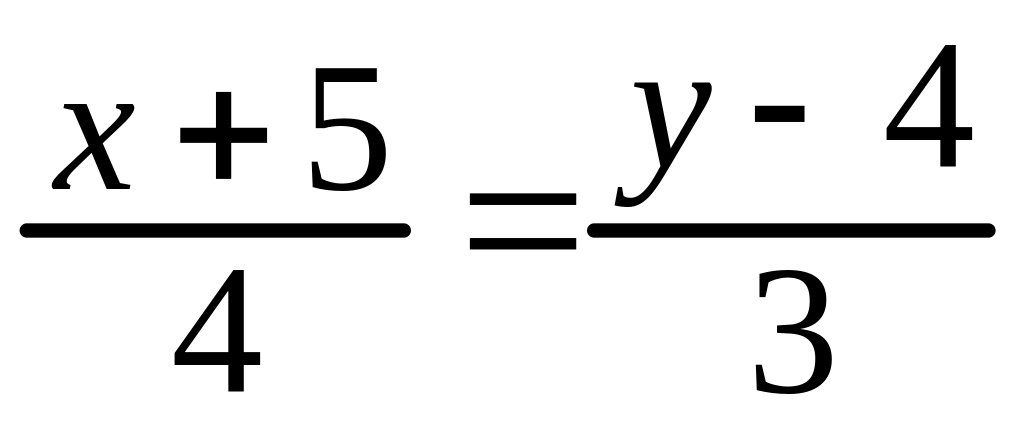
19.
Определить
отклонение точки М(2;3)
от
прямой
20.
Даны точки A(–1;
2), В(6;
–8). Определить, пересекаются ли прямая
и отрезок АВ.
21. Даны вершины треугольника: A(2; 2), В(–2; –8) и С(–6 ;–2). Составить уравнения медиан треугольника.
22. Даны вершины треугольника: A(0; 1); B(6; 5) и C(12; –1). Составить уравнение высоты треугольника, проведенной из вершины С.
23. Даны стороны треугольника: x+ 3y –7 = 0 (AB), 4x – у – 2 = 0 (ВС), 6х + 8y –35 = 0 (АС). Найти длину высоты, проведенной из вершины В.
24. Составить уравнения биссектрис углов между прямыми х + у – 5 = 0 и 7х–у –19 = 0.
25. Даны вершины треугольника: А(1; 1), В(10; 13), С(13; 6). Составить уравнение биссектрисы угла А.
26. Составить уравнения прямых, проходящих через точку М(5; 1) и образующих с прямой 2х +у –4 = 0 угол .
27.
Показать, что треугольник со сторонами
,
и
равнобедренный. Найти угол при его
вершине.
28. Даны последовательные вершины параллелограмма: А(0; 0), В(1; 3), С(7;1). Найти угол между его диагоналями и показать, что этот параллелограмм является прямоугольником.