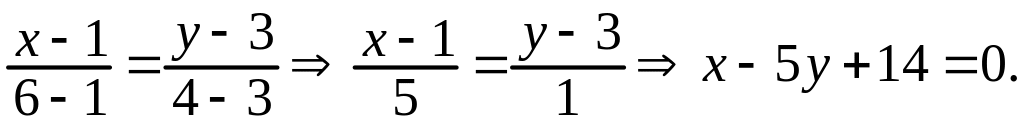Г ОУ ВПО Московской области Международный университет природы, общества и человека «Дубна»

ФИЛИАЛ «КОТЕЛЬНИКИ»

В.С. Кривошеева, в.А. Тайманов Уравнения прямой и плоскости

методические указания и варианты индивидуальных заданий

Рекомендовано к изданию научно-методическим советом

филиала «Котельники» университета «Дубна»

Котельники

2013

ББК 22.143

К 82-1

Рецензенты:

к.т.н., доцент кафедры прикладной математики Академии гражданской защиты МЧС России Бахтиярова О.Н.

Кривошеева В.С., Тайманов В.А.

К 82-1 Уравнения прямой и плоскости: Методические указания и варианты

индивидуальных заданий. – Котельники:

Международный университет природы, общества и человека

«Дубна», филиал «Котельники», 2013. – 88 с.

Методические указания предназначены для студентов изучающих линейную алгебру и аналитическую геометрию в рамках общего курса математики. Они должны помочь студентам лучше усвоить теоретический и практический материал по аналитической геометрии. В каждом разделе приводятся примеры решения типовых задач. В конце работы предлагается большое количество вариантов индивидуальных заданий по рассматриваемым темам.

Компьютерная верстка: А.В. Горячев, Е.В. Алешина

© В.С. Кривошеева, В.А. Тайманов, 2013

© Международный университет природы, общества

и человека «Дубна» филиал «Котельники», 2013

Содержание

Цель работы

Предлагаемые методические указания ставят своей целью помочь студентам усвоить теоретический и практический материал по теме «Уравнения прямой на плоскости и в пространстве. Уравнение плоскости». В них рассматриваются простейшие задачи аналитической геометрии на плоскости и в пространстве, основные уравнения прямых и плоскостей. В каждом разделе приводится решение типовых задач. Для закрепления материала студентам предлагается выполнить индивидуальное задание.

Уравнение прямой на плоскости

Будем считать, что на плоскости задана прямоугольная декартова система координат. Базисными векторами являются векторы и . Существенная часть утверждений, фактов и свойств, сформулированных ниже, справедливы для произвольной декартовой системы координат. Но многое из сформулированного, справедливо только для прямоугольной системы координат. Мы не будем уточнять, когда какой случай имеет место, но студентам следует иметь в виду, что все перечисленные ниже факты, безусловно справедливы только в том случае, когда базис системы координат является ортонормированным. Доказательства приведенных утверждений и полезные комментарии к ним можно найти в рекомендуемой ниже литературе.

Различные виды уравнения прямой на плоскости

В прямоугольной декартовой системе координат на плоскости каждая прямая линия может быть задана линейным уравнением

, где – постоянные, причем, . Последнее неравенство означает, что хотя бы одно из чисел А или В отлично от нуля.

Верно и обратное утверждение: каждое линейное уравнение , где , в прямоугольной декартовой системе координат на плоскости определяет прямую линию.

Поэтому уравнение

(1.1)

называется общим уравнением прямой на плоскости.

Фразу «прямая линия L задается уравнением

» следует понимать следующим образом: точка лежит на прямой L тогда и только тогда, когда при подстановке ее координат в уравнение получаем верное равенство, т.е. .

Нормальным вектором прямой называется любой ненулевой вектор, перпендикулярный данной прямой.

Направляющим вектором прямой называется любой ненулевой вектор, параллельный данной прямой.

Коэффициенты и уравнения имеют простой геометрический смысл:

одним из нормальных векторов прямой является вектор

; (1.2)

одним из направляющих векторов прямой является вектор

(1.3)

Таким образом, коэффициенты уравнения и определяют прямую с точностью до параллельности.

В некоторых случаях удобнее пользоваться не общим уравнением прямой, а уравнениями иного вида.

Уравнение

(1.4)

называется уравнением прямой с угловым коэффициентом. Коэффициент равен тангенсу угла между прямой и осью OX, а коэффициент равен ординате точки пересечения прямой с осью OY. Уравнением с угловым коэффициентом можно задавать только те прямые, которые имеют ровно одну точку пересечения с осью OY, т.е. прямые, непараллельные оси OY.

Уравнение

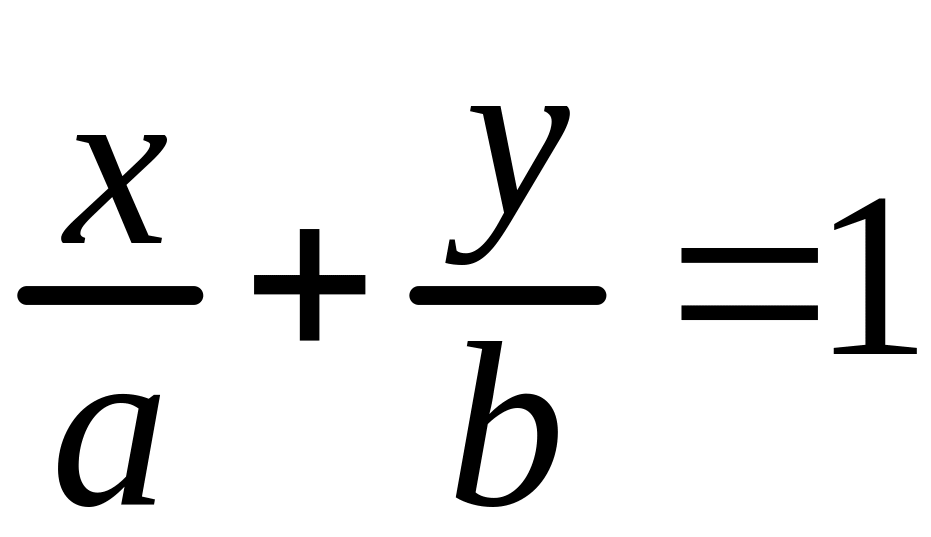(1.5)

называется уравнением прямой в отрезках. Коэффициент равен абсциссе точки пересечения прямой с осью OX, а коэффициент равен ординате точки пересечения прямой с осью OY. Уравнением в отрезках можно задавать только те прямые, которые имеют ровно одну точку пересечения с каждой из осей и не проходят через начало координат.

Уравнение

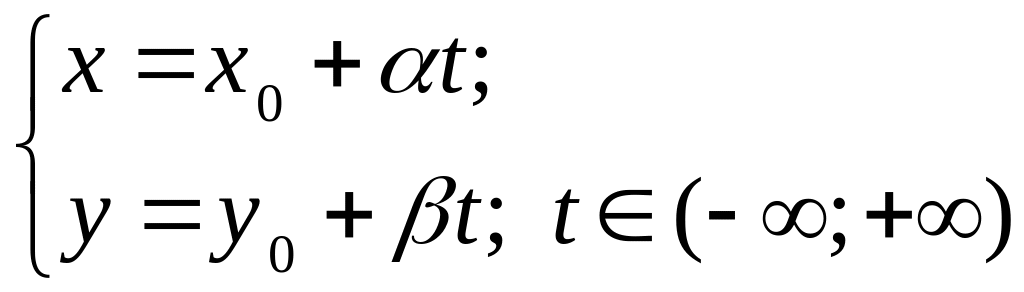(1.6)

называется параметрическим уравнением прямой. Вектор является направляющим вектором прямой, точка лежит на прямой, а параметр изменяется от . Подставляя различные значения параметра в параметрическое уравнение прямой, можно получать координаты различных точек прямой. Параметрическим уравнением можно задать любую прямую на плоскости.

Уравнение

(1.7)

называется параметрическим уравнением прямой в векторной форме. Вектор является направляющим вектором прямой, вектор является радиус-вектором точки , которая лежит на прямой, а параметр изменяется от . Подставляя различные значения параметра в параметрическое уравнение прямой в векторной форме, можно получать радиус-векторы различных точек прямой. Уравнением такого вида можно задать любую прямую на плоскости.

Отметим, что параметрическое уравнение прямой является просто покоординатной записью параметрического уравнения прямой в векторной форме.

Уравнение

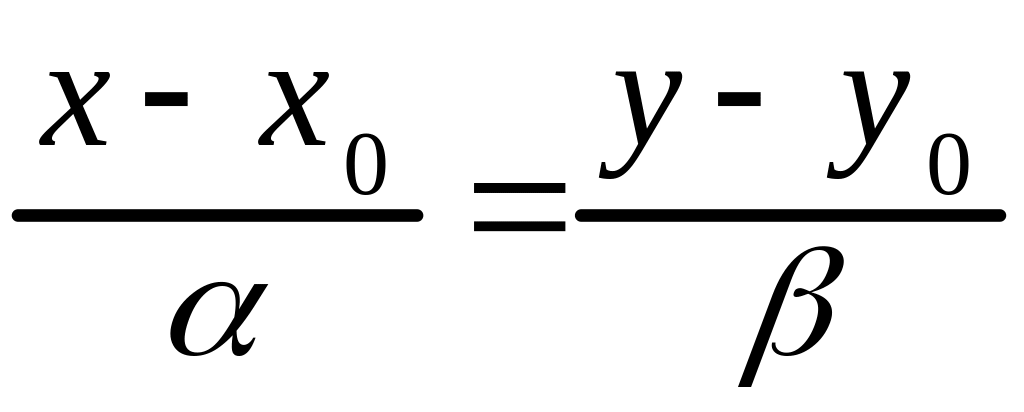(1.8)

называется каноническим уравнением прямой. Вектор является направляющим вектором прямой, точка лежит на прямой. Если одна из координат направляющего вектора равна 0, то числитель соответствующей дроби в уравнении тоже равен 0, и каноническое уравнение в этом случае следует рассматривать как формальную запись уравнения . Каноническим уравнением можно задать любую прямую на плоскости.

Нормальным уравнением прямой называется ее уравнение, написанное в виде

, (1.9)

где , – направляющие косинусы нормального вектора прямой, а – расстояние от прямой до начала координат. Нормальное уравнение получается из общего уравнения умножением обеих частей уравнения на 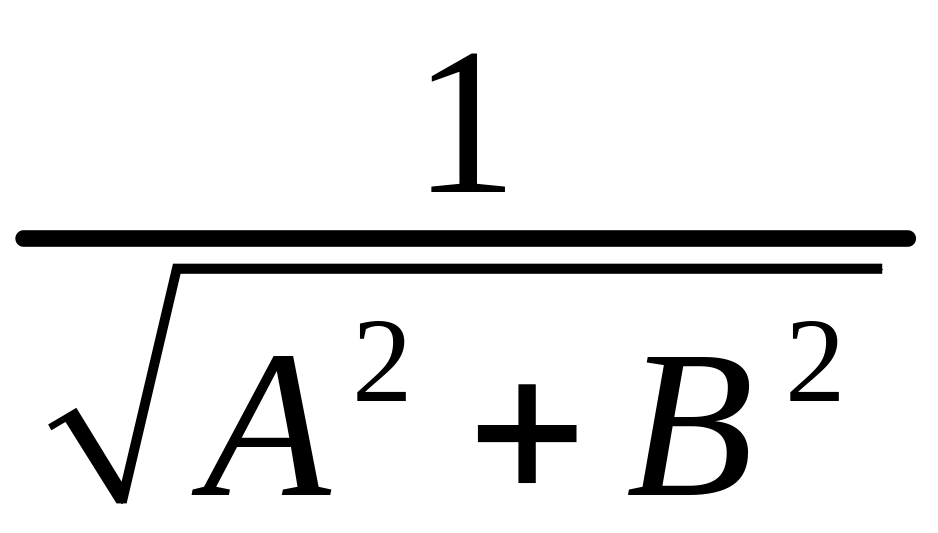(при ) или на 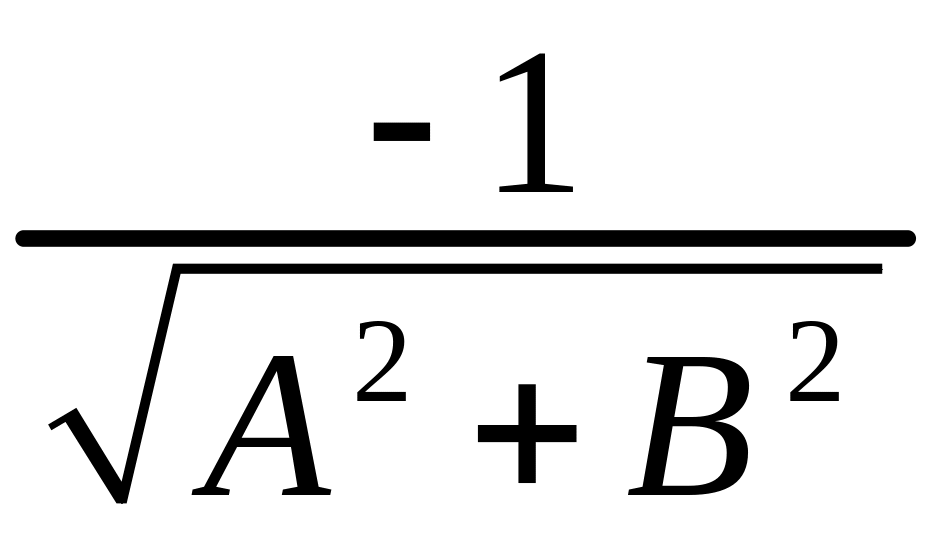(при ). Нормальным уравнением можно задать любую прямую на плоскости.

Очень часто на практике возникает следующая задача: требуется написать уравнение прямой, удовлетворяющей некоторым условиям. Приведем формулы, которые позволяют решать некоторые задачи такого типа.

Уравнение прямой, проходящей через точку

перпендикулярно вектору :

(1.10)

Каноническое уравнение прямой, проходящей через точку параллельно вектору :

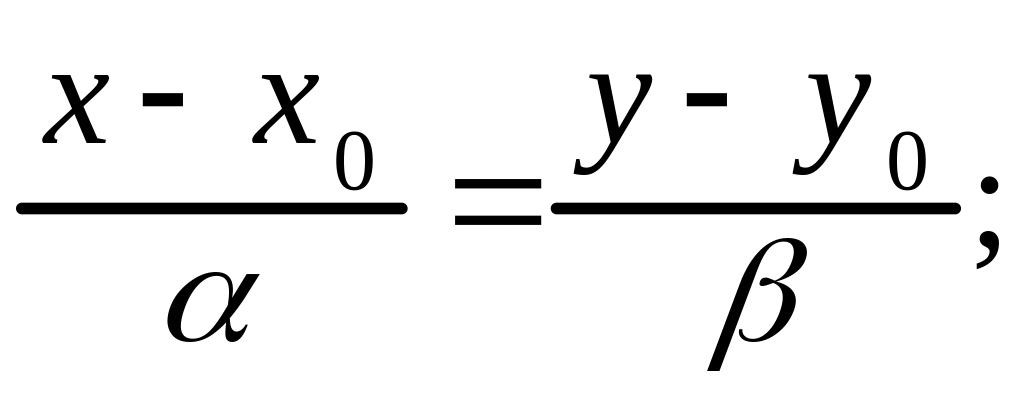(1.11)

Параметрическое уравнение прямой, проходящей через точку параллельно вектору :

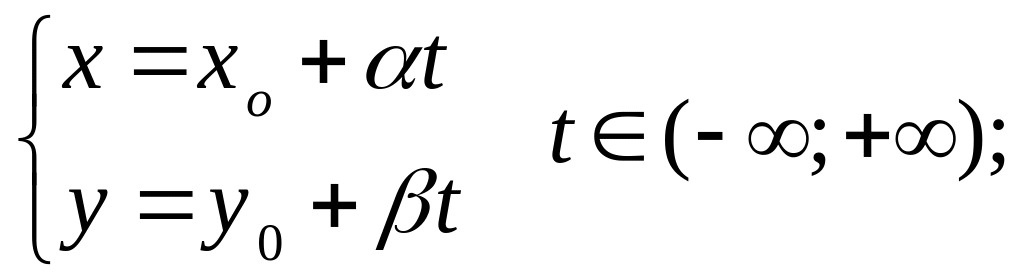(1.12)

Каноническое уравнение прямой, проходящей через точки и :

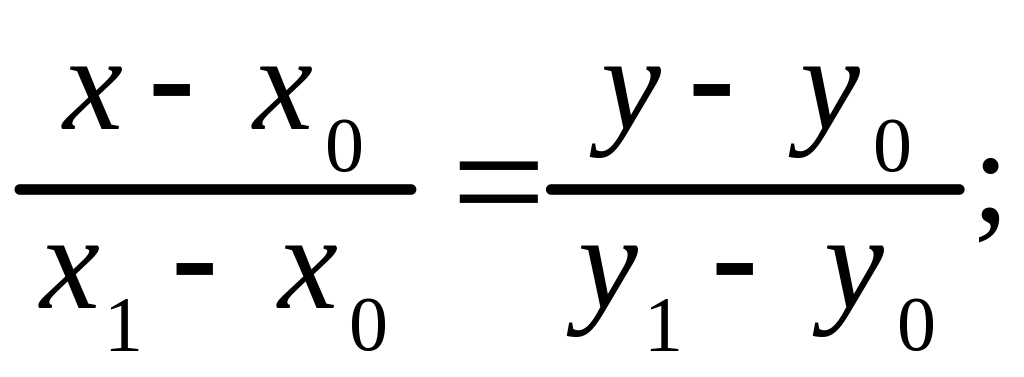(1.13)

Параметрическое уравнение прямой, проходящей через точки и

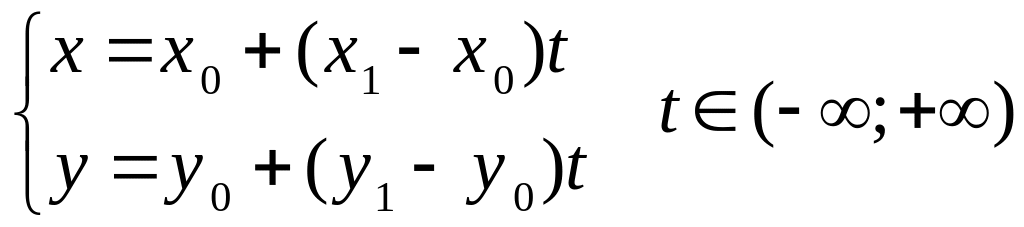(1.14)

Пример 1 . Составить уравнение координатной оси ОУ.

Решение. Получим решение несколькими способами.

1) Выберем в качестве нормального вектора прямой ОУ базисный вектор , а в качестве точки, принадлежащей прямой ОУ, — начало координат . Тогда уравнение искомой прямой, согласно (1.10), имеет вид

Раскрываем скобки и получаем: .

2) Если - нормальный вектор искомой прямой, то из (1.2) и (1.3) следует, что параллелен прямой. В качестве точки, принадлежащей прямой ОУ можно взять точку . Тогда уравнение искомой прямой, согласно (1.6), имеет вид:

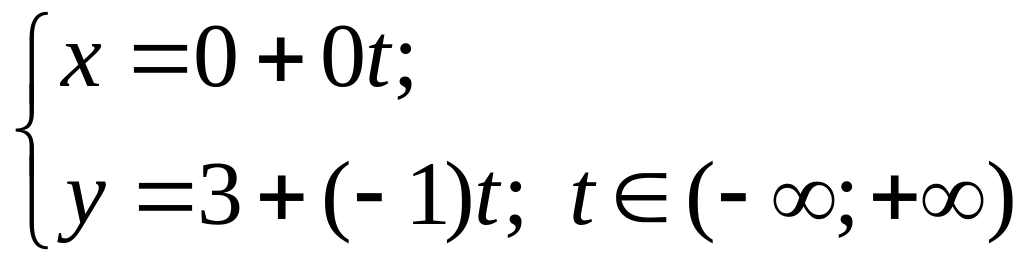
или, после упрощения:

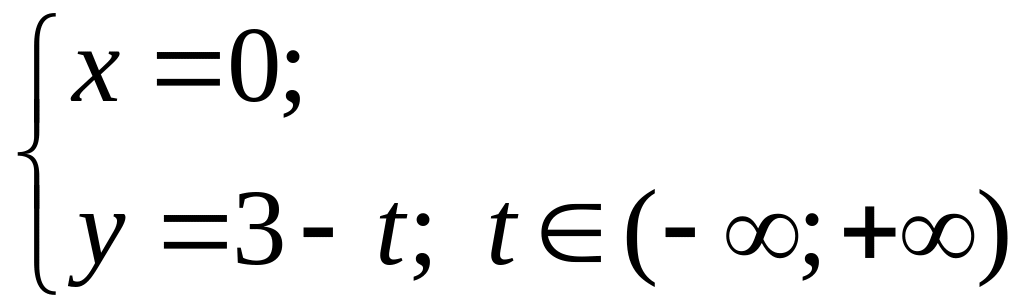
Из (1.11) тоже можно получить уравнение прямой:

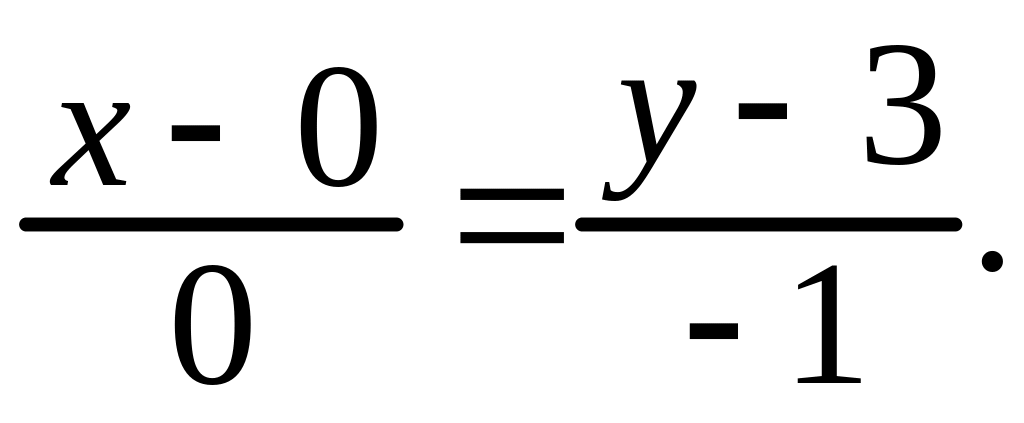
Преобразуем пропорцию и получаем:

или

Заметим, уравнения в отрезках или с угловым коэффициентом для этой прямой написать невозможно, поскольку она проходит через начало координат и параллельна оси OY.

Пример 2 . Составить уравнение прямой, проходящей через точку параллельно вектору и проверить, лежат ли точки и на этой прямой.

Решение. Составим уравнение в отрезках и с угловым коэффициентом (см. (1.4) и (1.5)) . Сначала применяем формулу (1.11):

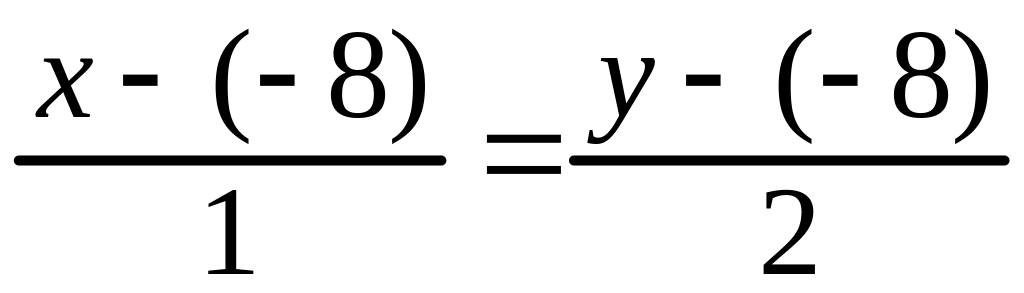
Преобразуем ее и получаем:

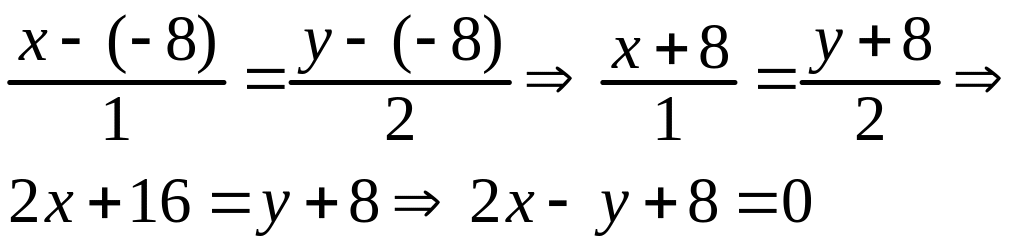
Это общее уравнение прямой. Переносим свободный член вправо, делим обе части на (–8), переносим все постоянные множители в знаменатели дробей и получаем уравнение в отрезках:

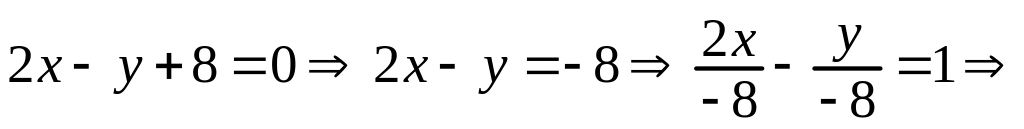
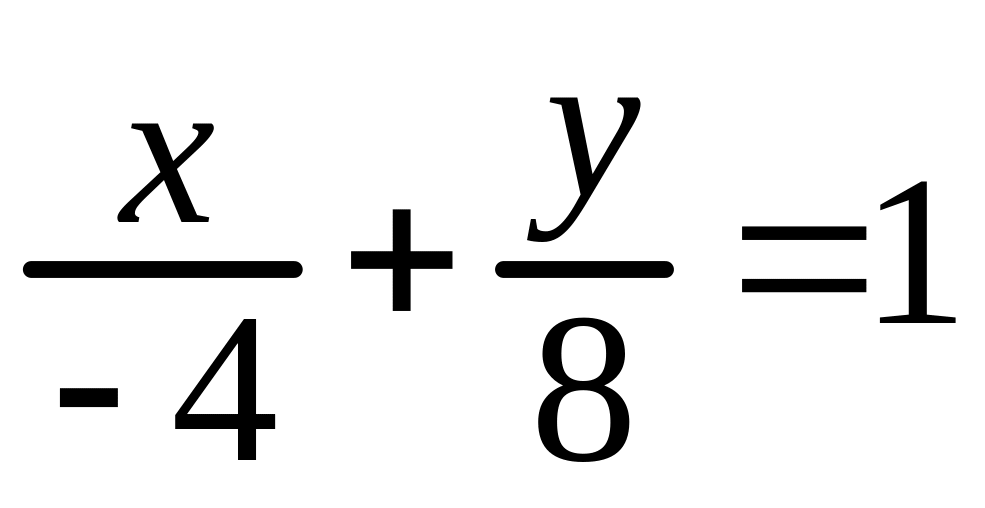
Выразив из общего уравнения прямой переменную , получаем уравнение с угловым коэффициентом:

Осталось проверить, лежат ли данные точки на прямой.

Подставляем координаты точек и в любое из уравнений прямой:

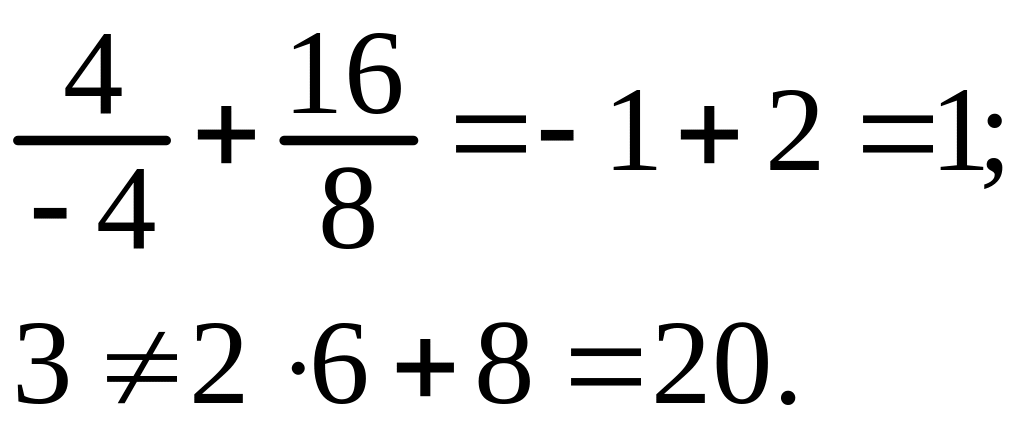
Следовательно, лежит на прямой, а – нет.

Пример 3 . Прямая задана уравнением с угловым коэффициентом Составить общее, каноническое и параметрическое уравнения этой прямой. Найти нормальный и направляющий векторы прямой.

Решение. Переносим вправо и получаем общее уравнение прямой Из (1.2) и (1.3) находим нормальный и направляющий векторы и . Находим какую-нибудь точку на . Для этого подставляем вместо произвольное значение, например, и находим соответствующее значение, Следовательно, проходит через точку . Теперь из (1.11) и (1.12) находим каноническое и параметрическое уравнения :

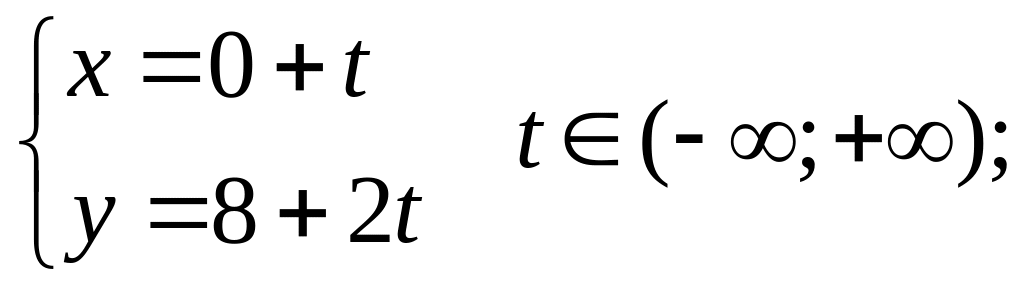
Пример 4 . Даны вершины треугольника A(1;3), B(4;7), C(8;1). Составить уравнения медианы AD и высоты AE.

Решение. Находим вектор и точку – середину стороны BC:

Осталось заметить, что АЕ – это прямая, проходящая через точку А перпендикулярно вектору , а AD – прямая, проходящая через точки A и D.

Из (1.10) и (1.13) получаем уравнения АЕ и AD: