3. Расчет изменения энергии Гиббса и Гельмгольца для различных процессов

1. Изменение энергий Гиббса и Гельмгольца при изменении температуры

Температурная зависимость энергий Гиббса и Гельмгольца от температуры определяется соотношениями:

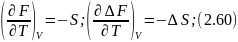
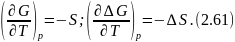
И в интегральной форме:

2. Изменение энергий Гиббса и Гельмгольца при изотермическом расширении или сжатии

Изменения энергий Гиббса и Гельмгольца при сжатии или расширении, когда Т = const, выражаются в дифференциальной форме уравнениями:

Для идеальных газов в интегральной форме:

Для конденсированных систем при умеренных давлениях

где – объем конденсированной фазы.

3. Изменение энергий Гиббса и Гельмгольца при фазовых превращениях

Изменение энергии Гиббса для фазовых переходов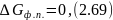

для испарения и возгонки (р = const)

для плавления и полиморфных превращений

4. Изменение энергий Гиббса и Гельмгольца при химической реакции

Рассмотрим различные способы:

1. Изменение энергии Гиббса можно рассчитать, используя стандартные энергии Гиббса образования реагентов и продуктов:

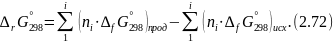
2. По определению, G = H – TS:

где 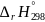и рассчитываем по уравнениям (1.16) и (1.18) соответственно.

При произвольной температуре изменение энергии Гиббса рассчитывают аналогично:

при этом температурные зависимости стандартной энтальпии и энтропии реакции определяются выражениями (1.26) и (2.25) соответственно.

3. Для расчета энергии Гиббса реакции удобно использовать так называемую приведенную энергию Гиббса или Ф-потенциал:

Приведенный потенциал имеет размерность [Дж·моль^-1·К^-1], численные значения этой функции для интересующего вещества при разных температурах можно найти в специализированных термодинамических справочниках. Для расчета стандартной энергии Гиббса реакции с помощью Ф-потенциала используют формулы:

Изменение энергии Гельмгольца химической реакции связано с энергией Гиббса соотношением

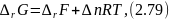
где Δn – изменение количества молей газообразных веществ в ходе реакции. Для реакций в конденсированной фазе эти две величины практически одинаковы

3. Зависимость термодинамических потенциалов от состава. Химический потенциал

При протекании химической реакции меняется число и вид частиц (молекул). Поэтому термодинамические потенциалы будут функциями не только своих естественных переменных, но и числа молей компонентов системы n_i. Тогда энергия Гиббса есть функция G = f(T, р, n₁, n₂,…), полный дифференциал которой равен

Обозначим

Величина – называется химическим потенциалом и представляет собой частную производную термодинамических потенциалов по количеству i-го компонента при фиксированных естественных переменных, т. е. он показывает, насколько изменяется соответствующий термодинамический потенциал при добавлении бесконечно малого количества i-го компонента к 1 молю раствора. Размерность Дж/моль.

Одно и тоже значение химического потенциала i-го компонента можно получить из зависимостей от числа молей n_i термодинамических потенциалов при постоянных естественных переменных:

С учетом введенных обозначений выражения для полных дифференциалов термодинамических потенциалов имеют вид:

Соответственно получаем

В выражении (2.88) знак равенства соответствует установлению термодинамического равновесия, знак «меньше» – самопроизвольному протеканию химической реакции.

Для того чтобы модно было использовать химический потенциал при решении практических задач, необходимо установить вид его зависимости от измеримых термодинамических переменных – температуры, давления и состава:

– Идеальные газовые смеси:

где – стандартный химический потенциал i-го газа, т. е. его потенциал в состоянии чистого вещества при заданной температуре и давлении 1 бар; – текущее парциальное давление газа.

– Реальные газовые смеси:

где – летучесть или фугитивность – давление, которое должна производить реальная система, чтобы оказывать такое же действие, как идеальная система; – коэффициент летучести используется для характеристики отклонения от идеального поведения.

– Идеальные конденсированные растворы:

где – мольная доля компонента в смеси.

– Реальные конденсированные растворы:

где – активность, которая может быть представлена в виде произведения мольной доли компонента на его коэффициент активности :

В нашем случае активность безразмерная величина. Также она может быть выражена через молярную или моляльную концентрации (активность будет иметь размерность концентрации), тогда будут изменяться значения коэффициентов активности.

Коэффициенты активности – безразмерные величины, они характеризуют работу, которую надо совершить при перемещении i-го компонента из идеального раствора в реальный при постоянной температуре, давлении и концентрации.