Сумма последовательных натуральных чисел.
Докажите,
что:
.
Решение.
При n =
1 равенство примет вид 
,1=1,
следовательно, P(1)
истинно. Предположим, что данное равенство
справедливо для некоторого n>1.
Следует
проверить (доказать), что P(n +
1), то есть
истинно. Поскольку (используется предположение индукции)
Получим
то есть, P(n + 1) - истинное утверждение. Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
Задача о разрезании пиццы.
Сколько кусков пиццы можно получить, делая n прямолинейных разрезов ножом? Или в другой формулировке: каково максимальное число Ln областей, на которые плоскость делится n прямыми?
Новая n-я прямая (при n > 0) увеличивает число областей на к тогда и только тогда, когда рассекает k старых областей, а рассекает она к старых областей тогда и только тогда, когда пересекает прежние прямые в k—1 различных местах. Две прямые могут пересекаться не более чем в одной точке. Поэтому новая прямая может пересекать n — 1 старых прямых не более чем в n— 1 различных точках, а значит k<=n и тогда Ln<= Ln-1+n. Более того, легко показать по индукции, что в этой формуле можно достичь равенства. Мы проводим n-ю прямую так, чтобы она не была параллельна никакой другой (следовательно, она пересекает каждую из них) и так, чтобы она не проходила ни через одну из имеющихся точек пересечения (следовательно, она пересекает каждую из прямых в различных местах). Поэтому рекуррентное соотношение имеет вид:
(1.2)
Теперь
найдём прямую формулу. Угадать её здесь
несколько сложнее (1,2,4,7, 11,16...), поэтому
используем другой подход, основанный
на развёртывании рекурентного соотношения:
Доказательство равенств.
Требуется
доказать следующие равенства (запись
означает
)
:
;
;
Решение.
При n = 1 равенство примет вид: 2·1 - 1 = 12 или 1=1, то есть, P(1) истинно. Допустим, что 1 + 3 + 5 + ... + (2n - 1) = n2 и докажем, что имеет место P(n + 1): 1 + 3 + 5 + ... + (2n - 1) + (2(n + 1) - 1) = (n + 1)2 или 1 + 3 +... + (2n - 1) + (2n + 1) = (n + 1)2. Используя предположение индукции: 1 + 3 +... + (2n - 1) + (2n + 1) = n2 + (2n + 1) = (n + 1)2. Таким образом, P(n + 1) истинно и, следовательно, требуемое равенство доказано.
При n = 1 равенство истинно: 1=1. Допустим, что оно истинно при некотором n>1, и покажем, что
.Действительно,
и,
так как 2n2 +
7n +
6 = (2n +
3)(n +
2), то
, и, следовательно, исходное равенство
справедливо для любого натурального n.
Доказательство неравенств.
Доказать неравенства:
|
|
|
|
|
|
Решение.
Таким образом, если P(n) истинно, то и P(n + 1) истинно, следовательно, согласно принципу математической индукции, неравенство Бернулли справедливо.
1) x1 = x2 = ... = xn = xn+1 = 1. Тогда сумма этих чисел равна (n + 1), и требуемое неравество выполняется; 2) хотя бы одно число отлично от единицы, пусть, например, больше единицы. Тогда, поскольку x1x2· ... ·xn·xn + 1 = 1, существует еще хhотя бы одно число, отличное от единицы (точнее, меньше единицы). Пусть xn + 1 > 1 и xn < 1. Рассмотрим n положительных чисел x1,x2,...,xn-1,(xn·xn+1). Произведение этих чисел равно единице, и, согласно гипотезе, x1 + x2 + ... + xn-1 + xnxn + 1 ≥ n. Последнее неравенство переписывается следующим образом: x1 + x2 + ... + xn-1 + xnxn+1 + xn + xn+1 ≥ n + xn + xn+1 или x1 + x2 + ... + xn-1 + xn + xn+1 ≥ n + xn + xn+1 - xnxn+1. Поскольку (1 - xn)(xn+1 - 1) > 0, то n + xn + xn+1 - xnxn+1 = n + 1 + xn+1(1 - xn) - 1 + xn = n + 1 + (1 - xn)(xn+1 - 1) ≥ n + 1. Значит, x1 + x2 + ... + xn + xn+1 ≥ n+1, то есть, если P(n) справедливо, то и P(n + 1) справедливо. Неравенство доказано.
|
|
.
,
где xi >
0,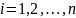 
, n ≥
2.
. Поскольку:
,
то по (2):
,
откуда
