117

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ПОЛТАВСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ ІМЕНІ ЮРІЯ КОНДРАТЮКА

КАФЕДРА НАРИСНОЇ ГЕОМЕТРІ ТА ГРАФІКИ

КОНСПЕКТ ЛЕКЦІЙ

НАРИСНА ГЕОМЕТРІЯ

Для студентів напрямів підготовки: 6.050304 – «Нафтогазова справа», 6.050301 – «Гірництво», 6.060103 – «Гідротехніка (водні ресурси)», 6.040106 – «Екологія, охорона навколишнього середовища та збалансоване природокористування», 6.050601 – «Теплоенергетика».

ПОЛТАВА, 2015

УДК 744

ББК 30.11

В75

Рекомендовано до друку вченою радою Полтавського національного технічного університету імені Юрія Кондратюка

Протокол

Рецензент: к.т.н., доц. Усенко В.Г.

Воронцов О.В.

Нарисна геометрія : конспект лекцій

Полтава : ПолтНТУ, 2015 – 110 с.

Конспект лекцій розраховано на студентів першого курсу напрямів підготовки 6.050601 – Теплоенергетика, денної форми навчання, які володіють знаннями з математики, в першу чергу з елементарної геометрії, в обсязі середньої школи.

Лекційний матеріал підготований відповідно до навчальної програми та складається з 8 лекцій.

Воронцов О.В.., 2015

Прийнята система скорочень і позначень

І. ПОЗНАЧЕННЯ ГЕОМЕТРИЧНИХ ОБРАЗІВ У ПРОСТОРІ

1.Точки

А, В, С, … – великі букви латинського алфавіту;

1, 2, 3, … – арабські цифри.

2. Лінії

а, b, c, … – малі букви латинського алфавіту;

h – тільки горизонтальна пряма;

f – тільки фронтальна пряма;

р – тільки профільна пряма;

АВ, (АВ) – пряма, яка визначається точками А і В;

[А,В] – відрізок прямої, який обмежений точками А і В.

3. Площини і поверхні

Г, Δ, Ω, Σ, Θ, Φ, … – великі букви грецького алфавіту;

П₁, П₂, П₃, П₄, … – площини проекцій з відповідним індексом;

Σ (А, В, С) – площина, що задана точками А, В, С;

Σ (А, m) – площина, що задана точкою А і прямою m;

Σ (d II m) – площина, що задана паралельними прямими d і m;

Σ (а ∩ с) – площина, що задана прямими а і с, які перетинаються;

Σ (Δ АВС) – площина, що задана трикутним відсіком АВС.

4. Кути

α, β, γ, … – малі букви грецького алфавіту;

а ^ с – кут між прямими а і с;

b ^ Г – кут між прямою b і площиною Г;

Σ ^ Г – кут між площинами Σ і Г.

5. Натуральні величини, довжина, відстань

|А, В| – відстань між точками А і В, довжина відрізка [АВ];

|А, b| – відстань від точки А до прямої b;

|а II с| – відстань між паралельними прямими а і с;

|Σ II Г| – відстань між паралельними площинами Σ і Г;

|d  b| – відстань між мимобіжними прямими;

|Δ ABC| – натуральна величина трикутника АВС;

|Σ ^ Г| – величина кута між площинами Σ і Г;

|а ^ с| – величина кута між прямими а і с;

ІІ. ПОЗНАЧЕННЯ ГЕОМЕТРИЧНИХ ЕЛЕМЕНТІВ КРЕСЛЕННЯ

1. Проекції геометричних елементів

Проекції геометричних елементів позначаються тими ж знаками, як і у просторі, з додаванням підрядкового індексу, який відповідає індексу площини проекцій:

А₁, А₂, А₃, …, 1₁, 1₂, 1₃, … – проекції точок;

а₁, а₂₂, а₃, …, h₁, h₂, f₁, f₂,… – проекції ліній;

Г₁, Г₂, Σ₁, Σ₂, … – проекції проецюючих поверхонь.

2. Позначення залежностей і інші символи

≡ – тотожно збігаються;

= – рівність, результат дії;

II – паралельність;

 – перпендикулярність;

∩ – перетин;

∪– з'єднання;

 – мимобіжність;

_ – належність елемента;

_{ – належність точки;}

_{ – не належить і т.п.}

3. Осі проекцій на комплексному кресленні

Х₁₂ – вісь проекцій в системі площин проекцій (П₁, П₂);

Y₁₃ – вісь проекцій в системі площин проекцій (П₁, П₃);

Z₂₃ – вісь проекцій в системі площин проекцій (П₂, П₃);

Х_iy – вісь проекцій в системі площин проекцій (П_і, П_у).

4. Лінії зв’язку

(А₁А₂) – вертикальна лінія зв’язку (лінія зв’язку в системі площин проекцій П₁ і П₂);

(А₂А₃) – горизонтальна лінія зв’язку (лінія зв’язку в системі площин проекцій П₂ і П₃).

ЛЕКЦІЯ 1.

ВСТУП. МЕТОД ПРОЕКЦІЙ.

КОМПЛЕКСНЕ КРЕСЛЕННЯ ТОЧКИ.

План.

1. Предмет і метод нарисної геометрії.

2. Центральне і паралельне проеціювання. Властивості проекцій.

3. Двокартинне комплексне креслення точки.

4. Проекції точки на три площини.

5. Ортогональні проекції і система прямокутних координат.

6. Конкуруючі точки.

7. Точка в квадрантах і октантах простору.

1. Інженерна графіка відноситься до дисциплін, які складають основу загально-інженерної підготовки спеціалістів з вищою освітою і складається з двох дисциплін – нарисної геометрії та технічного креслення. Метою курсу інженерної графіки є одержання знань, необхідних інженеру для втілення технічних думок з допомогою креслення, а також розуміння конструкції та принципу роботи представленого на кресленні технічного виробу.

Нарисна геометрія, як навчальна дисципліна є теорією відображення на площині фігур розташованих у просторі, та операцій над нами.

Предметом нарисної геометрії є виклад і обґрунтування методів побудови зображень просторових форм на площині і способів розв'язання задач геометричного характеру за заданими зображеннями.

2. Правила побудови зображень, які викладаються в нарисній геометрії ґрунтуються на методі проеціювання (проектування). Слово “проекція” – латинське, що в перекладі означає “кинути вперед”.

Креслення, які виконуються в нарисній геометрії, називають проекційними кресленнями. Вони мають містити в собі геометричну інформацію про форму та розміри просторової фігури (оригіналу), бути виконані з дотриманням єдності умовностей, прийнятих при виконанні зображень, та відповідати вимогам зворотності, наочності, простоти та точності. При побудові цих креслень широко використовуються проекційні властивості предметів.

Формоутворюючими елементами простору є основні геометричні фігури – точка, пряма і площина, з яких утворюються більш складні фігури.

Н а рис. 1.1 показано приклад побудови зображення точки - найпростішого елементу будь-якої геометричної форми, де точка А – оригінал, пряма t – проекційний промінь (проекційна пряма), площина  – площина проекцій, точка А_n – зображення точки А на площині , тобто проекція точки А, (АА_n – проецюючий відрізок).

Залежно від способу проведення проекційних променів проекції поділяють на центральні і паралельні.

Ідею центрального проеціювання видно з рис. 1.2, рис. 1.3.

П

Рис.1.3. Центральне проеціювання об’ємної фігури

ри цьому задаються фіксованим центром (полюсом) проеціювання S з якого виходять проекційні промені через усі найбільш характерні точки предмета до перетину їх з площиною проекцій. Сполучаючи точки перетину отримують центральну проекцію оригіналу.

Рис.1.2. Центральне проеціювання

 АВС

Властивості центральних проекцій:

1. Проекція точки є точка.

2. Проекція відрізка є відрізок.

3. Проекція площини є площина.

4. Проекція проецюючого відрізка є точка.

5. Проекція проецюючої площини є відрізок

Я

Рис.1.4. Паралельне проеціювання

кщо центр проекцій S віддалити в нескінченність, то на кінцевому відрізку проецюючі промені будуть паралельні між собою (тобто задається напрямок проеціювання, а не центр проекцій). Такий вид проеціювання називається паралельним (рис. 1.4).

Паралельні проекції поділяють на прямокутні і косокутні. Якщо проецюючі промені перпендикулярні до площини проекцій то такий спосіб проеціювання називається прямо-кутним, або ортогональним (рис.1.6).

Відмітимо інваріантні (незмінні) властивості, які відповідні паралельному ортогональному проеціюванню:

1. Всі властивості центрального проеціювання.

2. Проекції паралельних прямих паралельні.

3. Якщо точка D розділяє відрізок АВ в деякому співвідношенні (рис.1.5), то її проекція ділить проекцію відрізка в такому ж співвідношенні:

А D / DВ = А₀D₀ / D₀В₀.

4. Проекція точки перетину двох прямих являється точкою перетину проекцій цих прямих.

5. Плоска багатокутна фігура проецюється у фігуру з такою самою кількістю кутів.

6. При перенесенні плоскої фігури на паралельну площину її конфігурація не змінюється.

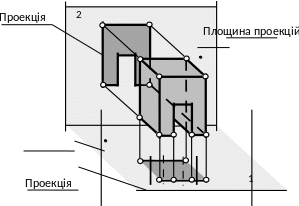
Рис.1.6. Паралельне ортогональне проеціювання

Якщо кут нахилу проецюючих променів не дорівнює 90⁰, то така паралельна проекція називається косокутною.

3 . Одна прямокутна проекція точки не визначає її положення в просторі. Його можна визначити сукупністю двох прямокутних проекцій (горизонтальної А₁ та фронтальної А₂) на дві взаємно перпендикулярні площини проекцій (горизонтальну площину проекцій ₁ та фронтальну площину проек-цій ₂) (рис.1.7.)

П₁ – горизонтальна площина проекцій; П₂ – фронтальна площина проекцій; Х₁₂ – вісь проекцій, лінія перетину площин П₁ і П₂; А₁ – горизонтальна проекція т. А; А₂ – фронтальна проекція т. А; А₁А₂ – вертикальна лінія зв’язку (з’єднує горизонтальну і фронтальну проекції т. А).

Для визначення положення точки за її паралельними проекціями необхідно мати дві паралельні проекції, одержані при двох напрямках проеціювання. Виходячи з того, що через точку можна провести тільки одну пряму, перпендикулярну до площини (тобто задати тільки один напрямок проеціювання S по відношенню до П₀), очевидно, що при ортогональному проеціюванні для одержання двох проекцій одної точки необхідно мати дві не паралельні площини проекцій. Оскільки П₁ П₂, а проецюючі промені S  П₁ і М  П₂, то лінія яка з’єднує проекції точки А  А₁А₂ перпендикулярна осі проекцій Х₁₂: А₂А₁₂Х₁₂; А₁А₁₂Х₁₂.

Креслення, що складається з кількох (мінімум двох) звязаних між собою проекцій зображувальної фігури, називається комплексним.

Вперше здійснювати проеціювання предметів на дві взаємно перпендикулярні площини запропонував французький вчений Гаспар Монж. Проеціювання при цьому залишається прямокутним.

Н езважаючи на багатовікову історію розвитку теорії і практики побудови зображень, реальні способи побудови графічних зображень наприкінці XVIII ст. ще не мали єдиної логічної системи. Лише геніальний французький вчений Гаспар Монж (фр. Gaspard Monge 1746–1818) із розрізнених методів і не завжди коректних способів побудови зображень створив нову галузь геометрії, систематизувавши й узагальнивши все те, що було запропоновано його попередниками.

Ця галузь геометрії стала називатися нарисною геометрією, суть якої вчений визначив так: “Мистецтво відображати на аркуші паперу, що має тільки два виміри, предмети, які мають три виміри”.

Подальший, після Гаспара Монжа, розвиток нарисної геометрії характеризується її деталізацією та застосуванням до вирішення різноманітних завдань науки та техніки.

Якщо обернути площину проекцій П₁ навколо осі Х₁₂ на кут 90⁰ до суміщення її з площиною проекцій П₂ (рис. 1.19-а), отримаємо плоске креслення, в якому проекції точки А₁ і А₂ розташовані на одному перпендикулярі до осі Х₁₂. Цей перпендикуляр називається вертикальною лінією зв’язку. Одержане креслення отримало назву епюр Монжа. При цьому відрізок А₂А₁₂ визначає відстань від точки А до площини П₁, а відрізок А₁А₁₂ визначає відстань від точки А до площини П₂.

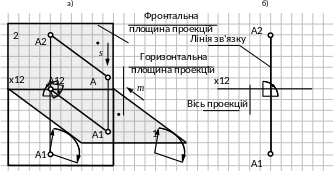
Рис.1.9. Утворення плоского креслення

Для простоти побудов надалі комплексне креслення точки в системі двох площин проекцій будемо зображати без границь площин проекцій П₁ та П₂ так, як показано на рисунку 1.9-б.

4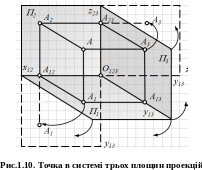 . Для з’ясування форми та розмірів складної фігури інколи двох проекцій недостатньо. В такому разі необхідно вводити в систему двох взаємно перпендикулярних площин проек-цій інші площини проекцій. Розглянемо введення в систему площин П₁ і П₂ третьої площини П₃, яка перпендикулярна до заданих площин П₁ і П₂. Ця площина називається профільною площиною проекцій (рис. 1.11).

Крім осі Х₁₂ з’являються дві нові осі: Y₁₃=П₁П₃; Z₂₃=П₂П₃. Літерою О₁₂₃ позначаємо точку перетину всіх трьох осей проекцій.

Плоске комплексне креслення утворюється шляхом суміщення площин П₁ і П₃ з П₂. Для суміщення П₁ з П₂ необхідно повернути її на 90° навколо осі Х₁₂ у напрямку руху годинникової стрілки; П₃ необхідно повернути навколо осі Z₂₃ на 90° у напрямку, протилежному руху годинникової стрілки. Пряма, яка сполучає А₂ і А₃ називається горизонтальною лінією зв’язку.

Проекції однієї і тієї ж точки на комплексному кресленні розташовуються не довільно, а знаходяться в проекційному зв’язку (рис. 1.11), який полягає в наступному:

1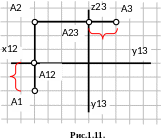 . Фронтальна і горизонтальна проекції точки завжди знаходяться на одній вертикальній лінії зв’язку (А₂А₁  OX).

2. Фронтальна і профільна проекції точки завжди знаходяться на одній горизонтальній лінії зв’язку (A₂A₃  OZ).

3. Відстань профільної проекції точки від осі OZ дорівнює відстані горизонтальної проекції від осі ОХ (|А₁А₁₂| = |А₃А₂₃|).

5 . У просторі є безліч точок, що займають різне положення відносно площин проекцій П₁, П₂ і П₃. В такому разі положення точки визначається дійсними величинами. Для цього в системі площин проекцій П₁, П₂, П₃ розміщується така ж система прямокутних декартових координат. Початок координатних осей суміщається з початком осей проекцій. Тепер положення кожної точки визначається трьома координатами – висотою, глибиною і широтою, які показують величини відстаней, на які точка віддалена від площин проекцій.

Висота точки (Z) визначає її відстань від площини проекцій П₁ – АА₁(на комплексному кресленні це відрізок А₁₂А₂).

Глибина точки (Y) визначає її відстань від площини проекцій П₂ – АА₂ (на комплексному кресленні це відрізок А₁₂А₁)

Широта точки (Х) визначає її відстань від площини проекцій П₃ – АА₃ (на комплексному кресленні це відрізок А₁₂О₁₂₃).

Між координатами точки та її ортогональними проекціями існує зв’язок: координата Х визначає положення вертикальної лінії зв’язку; Y – горизонтальної проекції точки; Z – фронтальної проекції точки.

6. Точки, проекції яких хоча б на одну із площин проекцій збігаються (точки, які лежать на одному проецюючому промені) називаються конкуруючими. Так, точка А знаходиться над точкою В (рис. 1.13-а), а точка D знаходиться перед точкою С (рис. 1.13-б).

Конкуруючі точки застосовуються при визначенні видимості непрозорих фігур згідно правила:

1) з двох конкуруючих точок в горизонтальній проекції видима та, висота якої більша;

2) з двох конкуруючих точок у фронтальній проекції видима та, глибина якої більша;

3) з двох конкуруючих точок у профільній проекції видима та, широта якої більша.

а) б)

Рис.1.14. Конкуруючі точки на плоскому кресленні

7. Площини проекцій П₁ і П₂ ділять простір на чотири двогранні кути, які називають квадрантами (рис. 1.14-а).

Точка може розташовуватись в одному із чотирьох квадрантів. Тоді її проекції на комплексному кресленні займають різні положення (рис. 1.14-б). Т. А - І квадрант; т. В - ІІ квадрант; т. С - ІІІ квадрант; т. D - ІV квадрант.

а) б)

Рис.1.14. Точки в квандрантах простору

Рис.1. 15. Нумерація октантів простору

Площини проекцій П₁, П₂ і П₃ ділять простір на вісім тригранних кутів, які називають октантами (рис. 1.15).

Додатними напрямками осей вважають:

- для осі Х - ліворуч від початку координат;

- для осі Y - в бік глядача від площини П₂;

- для осі Z - вгору від площини П₁.

Приймаючи для відліку координат точки систему знаків, яка вказана на рисунку, отримаємо таблицю 1.1 для визначення знаку координат в октантах простору.

Таблиця 1.1.

Октант		1	2	3	4	5	6	7	8
Знаки координат	ОX	+	+	+	+	-	-	-	-
	ОY	+	-	-	+	+	-	-	+
	ОZ	+	+	-	-	+	+	-	-