11. По типу ошибки в статическом режиме:

- статические САУ (регулируемая величина y(t) при постоянном задающем (возмущающем) воздействии по окончании переходного процесса принимает значение, пропорциональное воздействию, т.е. между входной и выходной величинами устройства имеется строго определенная функциональная связь y = f(x), которую называют статической характеристикой);

- астатические САУ (при внешнем воздействии по окончании переходного процесса значение регулируемой величины устанавливается равным заданному, т.е. система в установившемся режиме стремится к нулевому значению разницы между заданным и текущим значением регулируемой величины).

12) По характеру переходных процессов:

- устойчивые системы;

- неустойчивые системы;

- нейтральные системы.

13) По способу настройки:

- экстремальные САУ (требуется, чтобы выходная величина всегда принимала

экстремальное значение из всех возможных, которое заранее не определено и может

непредсказуемо изменяться; система выполняет небольшие пробные движения и

анализирует реакцию на них выходной величины, после чего вырабатывается

управляющее воздействие, приближающее выходную величину к экстремуму);

- оптимальные САУ (более сложный вариант экстремальных систем; здесь происходит

сложная обработка о всей информации, поэтому основное отличие этих систем – наличие

ЭВМ);

- адаптивные САУ (самонастраивающиеся и самоорганизующиеся).

Уравнения движения

В общем случае уравнения ММ объекта или системы управления, устанавливающие взаимосвязь между входными и выходными переменными, называются уравнениями движения.

Уравнения, описывающие поведение системы в установившемся режиме при постоянных воздействиях, называют уравнениями статики.

Уравнения, описывающие поведение системы при неустановившемся режиме при произвольных входных воздействиях, называются уравнениями динамики.

Все объекты можно разделить на 2 класса: объекты с сосредоточенными координатами, динамика которых описывается ОДУ, и объекты с распределенными координатами, динамика которых описывается ДУ в частных производных.

В качестве примера можно рассмотреть объект с сосредоточенными координатами, описываемый ДУ 2-го порядка:

F(y , y^’, y^’’, x , x^’) + f = 0 , (1)

где y – выходная переменная;

x, f – входные переменные.

При постоянных входных воздействиях x = x₀ , f = f₀ с течением времени выходная величина принимает постоянное значение y = y₀ и уравнение (1) преобразуется к виду:

F(y₀ , 0, 0, x₀ , 0) + f₀ = 0

Это уравнение статики.

Статический режим можно характеризовать с помощью статических характеристик.

Статической характеристикой объекта (системы) называется зависимость выходной величины от входной в статическом режиме.

Статическую характеристику можно построить экспериментально, если подавать на вход объекта постоянные воздействия и замерять выходную переменную после окончания переходного процесса. Если объект имеет несколько входов, то он характеризуется семейством статических характеристик. В свою очередь, сама статическая характеристика характеризуется коэффициентом k = dy/dx . Для объектов с нелинейной статической характеристикой коэффициент k является переменной величиной, для объектов с линейными статическими характеристиками коэффициент k – величина постоянная.

а) нелинейный объект; б) линейный объект

Статические характеристики объекта

В теории управления широко используется метод математических аналогий, согласно которому различные по физической природе объекты описываются однотипными математическими зависимостями.

1. Гидравлический резервуар – типичный объект автоматического

управления, в котором имеется приток и сток жидкости.

а) принципиальная схема; б) структурная схема

Гидравлическая емкость

Уровень жидкости H – выходная регулируемая величина.

Скорость притока воды в резервуар Q – регулирующее воздействие.

Расход воды из резервуара G – внешнее возмущение.

При постоянной степени открытия дросселя на притоке жидкости,

уровень определяется разностью (Q - G). По условиям работы объекта величина притока Q изменяется произвольно во времени.

Уравнение динамики, описывающее зависимость уровня H в переходном режиме от Q в соответствии с законом гидравлики записывается в виде

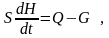
где S – площадь поперечного сечения резервуара.

Это уравнение – математическое описание объекта регулирования (гидравлической емкости), является ОДУ I-го порядка.

2. Химический реактор полного перемешивания.

Пусть в реакторе протекает химическая реакция типа A → B.

а) принципиальная схема; б) структурная схема

Химический реактор

При выводе уравнений приняты допущения:

1) в реакторе осуществляется идеальное перемешивание реакционной смеси, т.е. концентрация во всех точках реактора одинакова;

2) теплоемкость реакционной смеси постоянна и равна теплоемкости исходного реагента;

3) реакция протекает в изотермических условиях, т.е. температура в реакторе постоянна.

При этих допущениях реактор может рассматриваться как объект с сосредоточенными параметрами, материальный баланс которого имеет следующий вид:

Изменение Количество Количество Количество

количества реагента А, вещества А, вещества А,

вещества А = поступившего – вышедшего – вступившего

в реакторе в реактор во из реактора в реакцию

входном потоке

где V – объем реактора;

С_А – концентрация вещества А;

t – время;

q – объемный расход реагента А;

С_А0 – входная концентрация вещества А;

k – константа скорости реакции.

Таким образом, описание химического реактора идеального перемешивания с реакцией A → B осуществляется ОДУ I-го порядка.