9

3. Кінцеві автомати

Роспізнавачем (recognizer) мови називається програма, що одержує на вхід рядок х і відповідає "так", якщо х — речення мови, або, в протилежному випадку, "ні". У попередньому розділу було показано представлення граматик за допомогою регулярних виразів. Останні можна компілювати в роспізнавач шляхом побудови узагальненої діаграми переходів, називаної кінцевим автоматом. Такий автомат може бути детермінованим або недетермінованим (недетермінований автомат може мати більше одного переходу зі стану при тому самому ж вхідному символі).

Як детерміновані, так і недетерміновані кінцеві автомати здатні до розпізнавання точних регулярних множин. Таким чином, вони можуть розпізнавати все, що можуть позначати регулярні вирази. Однак детерміновані кінцеві автомати, які приводять до більш швидкого розпізнавання, звичайно більше за розміром, чим еквівалентні недетерміновані. У наступному розділі будуть розглянуті методи перетворення регулярних виразів в обидва типи кінцевих автоматів. Перетворення в недетермінований автомат більш очевидне, тому спочатку розглянемо саме цей тип автоматів.

У наведених нижче прикладах використається в першу чергу мова, задана регулярним виразом (a|b)*abb, що складається з множини всіх рядків з а й b, які закінчуються на abb. Подібні мови зустрічаються на практиці, наприклад, коментар у мові С, що починається з /*. Цей коментар являє собою будь-яку послідовність символів, що закінчується на */ з додатковою вимогою, щоб жоден власний префікс не закінчувався на * /.

3.1 Недетерміновані кінцеві автомати

Недетермінований кінцевий автомат (nondeterministic finite automaton, NFA), для якого далі в тексті використовується скорочення НКА, являє собою математичну модель, що складається з:

• множини станів S;

• множини вхідних символів X (символів вхідного алфавіту);

• функції переходів move, що відображає пари символ-стан на множину станів;

• стану s₀, відомого як стартовий (початковий);

• множини станів F, відомих як такі, що допускають, або припустимі стани (кінцеві).

НКА може представлятися у вигляді позначеного орієнтованого графа, так називаного графа переходів, вузли якого являють собою стани, а позначені дуги становлять функцію переходів. Такий граф схожий на діаграму переходів, однак один і той же самий символ може позначати два й більше переходи з одного стану, а деякі переходи можуть бути позначені спеціальним символом ε, як звичайним вхідним символом (ε-переходи).

Граф переходів для НКА, що розпізнає мову (a|b)*abb, показаний на рис. 3.1. Множина станів НКА — {0, 1, 2, 3}, а вхідний алфавіт— {а, b}. Стан 0 - стартовий, а заключний стан 3 представлено подвійним кружком.

Рис. 3.1. Недетермінований кінцевий автомат

При опису НКА скористаємося графом переходів. Як ми побачимо далі, функція переходів НКА може бути реалізована різними способами. Найпростіший з них — таблиця переходів, у якій рядки представляють стани, а стовпці — вхідні символи (і, при необхідності, ε). Запис у рядку i для символу а є множиною станів (або — на практиці — найчастіше покажчиком на множину станів), які можуть бути досягнуті переходом зі стану i при вхідному символі а. Таблиця переходів для НКА, що був наведений на рис. 3.1, показана на рис. 3.2.

Стан	Вхідний	символ
	a	b
0	{0,1}	{0}
1	–	{2}
2	–	{3}

Рис. 3.2. Таблиця переходів для кінцевого автомата на рис. 3.1

Подання автомата таблицею переходів добре тим, що забезпечує швидкий доступ до переходів з даного стану по даному символу. Разом з тим таблиця займає занадто багато місця, коли вхідний алфавіт великий і більшість переходів ведуть у порожню множину станів. Подання функції переходів у вигляді списку більш компактно, щоправда, у цьому випадку сповільнюється доступ до переходів. Очевидно, що кожне із цих подань легко перетворити в інше.

НКА допускає, або приймає (accept) вхідний рядок х (а цей рядок є припустимим) тоді й тільки тоді, коли в графі переходів існує деякий шлях від початкового стану до якого-небудь із заключних, такий, що мітки дуг цього шляху відповідають рядку х. НКА на рис. 3.1 допускає вхідні рядки abb, aabb, babb, aaabb, .... Наприклад, aabb допускається по шляху з 0 уздовж дуги а в стан 0, потім у стани 1, 2 й 3 уздовж дуг, позначених відповідно а,b і b.

Ш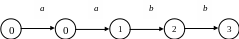 лях може бути представлений у вигляді послідовності переходів станів, так званих переміщень, або ходів (moves). Наступна діаграма показує переміщення, виконані для вхідного рядка aabb:

З агалом кажучи, у заключний стан може приводити більш ніж одна послідовність переміщень. Так, для вхідного рядка aabb можуть бути здійснені й деякі інші послідовності переміщень, що не приводять у заключний стан. Наприклад, для того ж вхідного рядка aabb може бути виконана наступна послідовність переміщень, що залишає нас у стані 0:

Мова, обумовлена НКА, являє собою множину вхідних рядків, що припускаються ним. Не так складно показати, що НКА на рис. 3.1 допускає рядок (a|b) *abb.

Приклад 3.1

На рис. 3.3 показаний НКА, що розпізнає рядок аа*|bb*. Рядок ааа допускається переміщеннями по станах 0, 1, 2, 2 й 2. Мітками відповідних дуг є ε, а, а й а, конкатенація яких дає рядок ааа, при цьому ε у результуючому рядку відсутній.

Рис. 3.3 Недетермінований кінцевий автомат, що допускає рядки аа*|bb*