3.3.2. Лавинно-пролетный диод

Основными представителями семейства лавинно-пролетных диодов являются диод Рида, асимметричный резкий p-n-переход, симметричный p-n-переход (диод с двумя дрейфовыми областями), диод с трехслойной базой (модифицированный диод Рида) и p–i–n-диод. Ниже рассмотрены статические характеристики этих диодов (распределение электрического поля, напряжение пробоя и эффекты пространственного заряда).

Рисунок 3.12 - Распределение примесей (а), напряженности электрического поля(б)

при пробое в p⁺-n-i-n⁺ -диоде Рида

На рисунке 3.12 приведены распределения примесей электрического поля в идеализированном диоде Рида (p⁺ – n – i – n⁺- или n⁺ – p – i – p⁺-диоде) при пробое. Эффективный коэффициент ударной ионизации равен

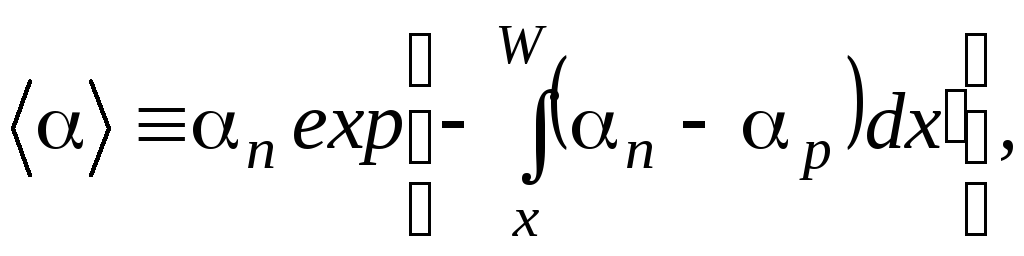(3.9)

где и– коэффициенты ударной ионизации электронов и дырок соответственно – ширина обедненной области.

Условие лавинного пробоя можно записать в виде

Из-за сильной зависимости коэффициентов ударной ионизации от напряженности электрического поля область лавинного умножения сильно локализована, т.е. практически весь процесс умножения носителей происходит в узком слое высокого поля от 0 до х_А , где х_А – ширина области умножения. Падение напряжения на области умножения обозначим V_A. Оптимальная плотность тока и максимальный к.п.д. лавинно-пролетных диодов сильно зависят как от х_А так и от V_A. Слой вне области умножения (х_А х называется областью дрейфа.

Существуют два предельных случая распределения примеси в диодах Рида. Если отсутствует область с концентрацией примеси N₂ , то это – резкий p⁺ – n-переход. Если же отсутствует область с концентрацией N₁ , то диод Рида выражается в p–i–n-диод, который иногда называют диодом Мисавы. На рисунке 3.13, а приведены статические характеристики диода с ассиметричным резким р – n-переходом. Область лавинного умножения сильно локализована. На рисунке 3.13, б приведены характеристики кремниевого диода с симметричным резким р – n-переходом. Область умножения расположены вблизи центра обедненной области. Небольшая асимметрия эффективного коэффициента ударной ионизации по отношению к точке, в которой напряженность электрического поля максимальна, связана с тем, что в кремнии исильно различаются.

Если , как это имеет место вGaP, эффективный коэффициент ионизации

и область лавинного умножения симметрична по отношению к точке .

На рисунке 3.14, а приведены статические характеристики модифицированной структуры Рида – диода с двухслойной базой, в котором концентрация N₂ существенно превышает соответствующую величину для диода Рида. Статические характеристики другой модификации – диода с трехслойной базой приведены на рисунке 3.14, б. В этом диоде «сгусток» заряда Q расположен в точке . Поскольку достаточно высокая напряженность электрического поля остается постоянной между точкамии, то максимальное поле может быть меньше, чем в диоде с двухслойной базой. Вp–i–n-диоде электрическое поле однородной во всей i-области при малых токах. В этом случае область лавинного умножения соответствует всей ширине слоя собственной концентрации

.

Рисунок 3.13 - Распределения примесей и напряженности электрического поля в диоде с ассиметричным резким p⁺ – n-переходом (диод с одной дрейфовой областью) (а) и вp⁺ – р – n – n⁺ -диоде с симметричным резкимр – n-переходом (диод с двумя дрейфовыми областями (б)

Напряжение пробоя для асимметричных резких p–n-переходов было рассмотрено в [1]. Можно воспользоваться этим методом для того, чтобы найти напряжения пробоя для других типов диодов. Для симметричных резких переходов (рисунок 3.14, б) напряжение пробоя определяется равенством

, (3.10)

где – величина максимальной напряженности электрического поля при. На рисунке 3.15 приведены максимальные напряженности электрического поля при пробое в симметричных и асимметричныхр – n-переходах из кремния и арсенида галлия с ориентаций (100). Если известна концентрация примеси, то напряжение пробоя можно найти из равенства (3.10), пользуясь графиками, приведенными на рисунке 3.15. Обратное напряжение при пробое равно (), где– контактная разность потенциалов, причем=в случае симметричных резких переходов (в работающих ЛПД величинойможно пренебрегать).

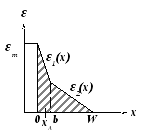
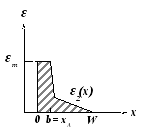
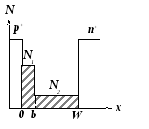
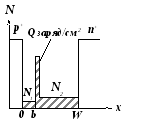
Рисунок 3.14 - Распределения примесей и напряженности электрического поля в

модифицированных диодах Рида: с двухслойной базой (а) и трехслойной базой (б)

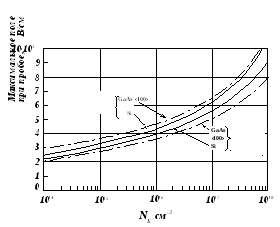
Рисунок 3.15 - Максимальная напряженность электрического поля при пробое как функция концентрации для асимметричных и симметричных резких переходов из SiиGaAs.

Напряжение пробоя и ширина обедненной области в диоде Рида и диоде с двухслойной базой определяются следующими равенствами:

(3.11)

(3.12)

Ширина обедненной области в диоде Рида ограничена толщиной эпитаксиального слоя, которая меньше величины, вычисленной с помощью равенства (6). Максимальная напряженность электрического поля при пробое в диоде Рида или диоде с двухслойной базой с точностью до 1% совпадает с соответствующей величиной для асимметричного резкого р – n-перехода с такой же концентрацией примеси N₁ при условии, что ширина области лавинного умножения . Следовательно, напряжение пробоя можно найти из равенства (3.11) и (3.12), используя величину максимальной напряженности электрического поля из графиков, приведенных на рисунке 3.16.

Рисунок 3.16 - Диод, смонтированный на медном теплоотводе, с металлическими слоями, используемыми для термокомпрессированного соединения золото – золото (а), упрощенная структура диода и теплоотвода (б)

При низких частотах характеристики ЛДП в непрерывном режиме генерации ограниченны в первую очередь температурным фактором, т.е. мощностью, которая может быть рассеяна в виде тепла в полупроводниковом кристалле. Типичный способ монтажа прибора показан на рисунке 3.16, а. Упрощенная структура диода и теплоотвода изображена на рисунке 3.16, б. Полное тепловое сопротивление для кругового источника тепла радиусов r на глубине d_s в кремнии равно

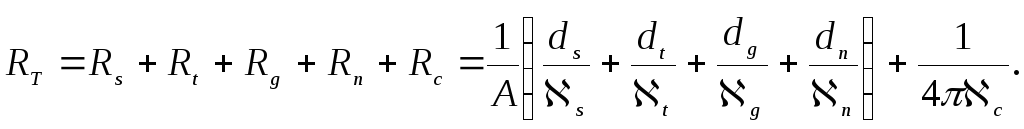(3.13)

Символы поясняются рисунком 3.16, б. Последнее слагаемое равно тепловому сопротивлению теплоотвода, занимающему бесконечное пространство. Предполагается, что теплопроводность алмаза при 300 К в 3 раза превышает соответствующую величину для меди, а значение теплопроводности кремния соответствует максимальной рабочей температуре 500 К (таблица 3.1). Из рисунка видно, что

Таблица 3.1.

Теплопроводность и типичные значения толщин слоев различных материалов для диода, работающего в диапазоне частот 15 – 18 ГГц при 300 К

Материал	Теплопроводность , Вт/см.К)	Толщина d, мкм	10-4см2.К/Вт
Кремний	0,80	3,00	3,80
Титан	0,16	0,02	0,13
Золото	3,00	12,50	4,20
Никель	0,71	0,20	0,28
Медь	3,90	-	-
Алмаз	20,00	-	-

алмазный теплоотвод уменьшает тепловое сопротивление приблизительно в 2 раза, а R_Т убывает с ростом площади диода.

Мощность Р , которая может быть рассеяна в виде тепла в диоде, должна быть равна мощности, которая может быть передана в теплоотвод. Поэтому Р равно , где- разность температурp–n-перехода и теплоотвода. Если реактивная проводимость (гдеостается постоянной, а основной вклад в тепловое сопротивление вносит полупроводник (в предположении, что), то для заданной величины

~(3.14)

В этих условиях величина генерируемой в непрерывном режиме мощности уменьшается пропорционально 1/f.