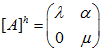1.2 Фазовая плоскость линейной однородной системы с постоянными коэффициентами

Здесь мы построим фaзовые траектории на фазовой плоскости системы с постоянными действительными коэффициентами:

Заметим, что начало координат (0,0) всегда является положением равновесия системы (1.9). Это положение равновесия тогда и только тогда является единственным, когда детерминант матрицы   отличен от нуля, или что то же, оба собственных значения этой матрицы отличны от нуля.

Рассмотрим скалярные величины x₁, x₂ как координатный столбец   вектора   в двумерном линейном пространстве  , в котором фиксирована некоторая ортогональная координатная система  ; матрица   задает линейный оператор  такой, что

Перепишем систему (1.9) в матричной форме:

а также в инвариантной форме:

I. Случай действительных и различных собственных значений

Допустим, что собственные значения матрицы A действительны, различны и отличны от нуля. Тогда, произвольное действительное решение   системы (1.12) в собственном базисе   оператора A имеет вид:

Здесь ₁,₂ - собственные значения оператора   - соответствующие собственные векторы, т.е.   - действительные константы.

Координаты ₁,₂ на фазовой плоскости P системы (1.9), вообще говоря, не являются прямоугольными, поэтому отобразим аффинно фазовую плоскость P на вспомогательную плоскость P^* так, чтобы линейно-независимые собственные векторы   перешли во взаимно ортогональные единичные векторы плоскости P^*, направленные соответственно по оси абcцисс и оси ординат (рис 1.5).

Тoчка   плоскости P перейдет при этом отображении в точку с теми же координатами ₁,₂, но относительно новой прямоугольной системы координат в плоскости P^*. Таким образом, траектория, заданная параметрическими уравнениями (1.13) в плоскости P перейдет в траекторию, заданную теми же уравнениями в прямоугольных координатах плоскости P^*. Мы начертим сперва траектории, заданные уравнениями (1.13) в плоскости P^*, а затем отобразим их обратно в плоскость P.

Наряду с фазовой траекторией (1.13) в плоскости P^* имеется траектория, задаваемая уравнениями

а также траектория, задаваемая уравнениями

Траектория (1.14) получается из траектории (1.13) зеркальным отображением относительно оси абcцисс, и траектория (1.15) - относительно оси ординат. Таким образом, указанные два зеркальных отображения оставляют картину траекторий на плоскости P^*инвариантной. Из этого следует, что если вычертить траектории в первом квадранте, то уже легко представить себе фазовую картину в плоскости P^*.

Значениям c₁ = c₂ = 0 соответствует положение равновесия (0,0). При c₁ > 0,  c₂ = 0 фазовая траектория находится на положительной полуоси абcцисс. При c₁ = 0,  c₂ > 0 фазовая траектория находится на положительной оси ординат.

Если ₁ < 0, то движение, описывающее положительную полуось абcцисс, протекает в направлении к началу координат, если же ₁ > 0, то движение это имеет противоположное направление - от начала координат. В первом случае точка движется неограничено приближаясь к началу координат, во втором - неограничено удаляясь в бесконечность. То же справедливо и относительно движения, описывающего положительную полуось ординат. Если константы c₁ и c₂ положительны, то фазовая траектория находится в первой четверти, не выходя на ее границу.

Для более детального описания фазового портрета следует рассмотреть несколько случаев.

А) Допустим, что собственные значения ₁,₂ имеют один знак и пусть для определенности

Рассмотрим случай, когда

При этих предположениях движение по положительной полуоси абcцисс направлено к началу координат, точно так же, как движение по положительной полуоси ординат. Далее, движение по произвольной фазовой траектории внутри первого квадранта состоит в асимптотическом приближении точки к началу координат, причем траектория при этом касается оси абcцисс в начале координат. Действительно, из параметрических уравнений траекторий (1.13) следует равенство

из которого ясен качественный характер поведения фазовой траектории. При t, стремящемся к , точка движется по фазовой кривой, удаляясь от положения равновесия (0,0). Эта фазовая картина называется устойчивым узлом. (рис. 1.6а)

Рассмотрим теперь случай, когда наряду с неравенством (1.16) выполнены неравенства:

При этом траектории остаются прежними, но движение по ним направлено (по сравнению с предыдущим случаем) в противоположном направлении. В этом случае мы имеем неустойчивый узел (рис. 1.6б)

В) Допустим, что собственные числа ₁ и ₂ имеют противоположные знаки. Пусть для определенности

В этом случае движение по положительной полуоси абcцисс идет к началу координат, а движение по положительной полуоси ординат - от начала координат. Из параметрических уравнений (1.13) получаем:

Таким образом, фазовые траектории, лежащие внутри первого квадранта, напоминают по своему виду гиперболы, а движение по ним происходит в направлении к началу координат вдоль оси абcцисс, и в направлении от начала вдоль оси ординат. Эта фазовая картина называется седлом. (рис 1.7)

II. Кратные собственные значения

Предположим, что матрица A системы (1.9) имеет лишь одно собственное значение  (кратности два). Тогда возможны два существенно различных случая.

Случай 1. Существует в плоскости   базис  , состоящий из двух собственных векторов оператора A: P  P:

Случай 2. Существует в плоскости   базис  , состоящий из серии, соответствующей собственному значению :

Докажем существование базиса в плоскости одного из видов (1.18) или (1.19). Пусть   - собственный вектор оператора A и   - произвольный вектор, не коллинеарный вектору  . Тогда мы имеем:

Отсюда видно, что оператор A имеет в базисе   матрицу:

так, что его собственными значениями являются  и  и поэтому  = . Если  = 0, то для базиса   выполнены соотношения (1.18). Если же   0, то заменив вектор   пропорциональным ему вектором  , мы получим базис, удовлетворяющий условиям (1.19).

В первом случае общее решение уравнения (1.12) записывается в виде:

При   0 каждое решение (1.20) ( при различных начальных значениях  ) описывает полупрямую, выходящую из начала координат. При  < 0 движение происходит в направлении к началу координат (рис. 1.8а), при  > 0 - от начала координат (рис. 1.8б)

В случае 2 произвольное решение уравнения (1.12) имеет вид:

Отсюда следует, что координаты решения   в базисе   выражается по формулам

Аффинное преобразование фазовой плоскости P, переводящее векторы   и   в единичные ортогональные векторы, направленные по осям координат плоскости P^*, переводит траектории плоскости P в траектории плоскости P^*, в которой уравнения (1.22) дают траектории уже в прямоугольных координатах.

Разберем случай   0. Пусть сначала  < 0. Рассмотрим траектории, заполняющие плоскость P^*, в этом случае. Из формул (1.22)видно, что наряду с траекториями (1.22), траекториями будут кривые с уравнениями:

Другими словами, фазовая картина в плоскости P^* симметрична относительно начала координат. Таким образом, достаточно рассмотреть все траектории в верхней полуплоскости. При c₁  0,  c₂ = 0 получаем две траектории: одну при c₁ > 0, другую - при c₁ < 0. Первая совпадает с положительной полуосью абсцисс, вторая - с отрицательной полуосью абсцисс; движение по обоим направлено к началу координат.

Рассмотрим далее траекторию соответствующую c₁ = 0,  c₂ > 0. Мы имеем:

При t = 0 получаем точку (0,c₂) на оси ординат. При t, возрастающем от нуля, точка движется по траектории

(получается из (1.23) после исключения t) сначала направо, затем налево, все время опускаясь вниз к началу координат, к которому она подходит по траектории, касающейся положительного направления оси абсцисс. При t, убывающем от нуля до , точка движется налево, одновременно поднимаясь вверх, однако налево быстрее, чем вверх, так что общая тенденция ее движения - в отрицательном направлении вдоль оси абсцисс. Если в уравнениях (1.23) придавать константе c₂ все положительные значения, то описанные таким образом фазовые траектории заполнят всю верхнюю полуплоскость. Мы имеем здесь устойчивый вырожденный узел (рис. 1.9).

Если  > 0, то вместо уравнения (1.24) мы получаем уравнение траектории в виде:

то есть данные траектории получаются из описанных выше путем зеркального отображения плоскости относительно оси ординат (рис. 1.10).

Движение по этим траекториям идет в противоположном направлении, т.е. от начала координат. Это - неустойчивый вырожденный узел.

III. Случай комплексных корней

Рассмотрим теперь случай, когда собственные числа матрицы A комплексны. Тогда они комплексно сопряжены и могут быть обозначены через  = + i,   =  i, причем   0.

Числа  и   являются собственными значениями оператора  , соответствующего матрице A.

Предложение 1.2.1 Оператор A представляет собой овеществление оператора   умножения на комплексное число . Точнее, плоскость   можно снабдить структурой комплексной прямой  , так что   и  .

Доказательство. Пусть   - комплексный собственный вектор оператора   с собственным значением  = + i. Векторы  и   образуют базис в  . Имеем с одной стороны:

и с другой -

откуда

Таким образом, оператор   в базисе   имеет матрицу:

В то же время оператор   умножения на  = + i в базисе 1,i имеет ту же матрицу (1.26). Итак, искомая комплексная структура на   получится, если принять   за 1 и   за i. Предложение доказано.

Таким образом, следует рассмотреть уравнение:

Мы знаем его решения:

где C - комплексная константа.

Перепишем уравнение (1.28) в полярных координатах, положив

Таким образом, получаем:

это есть уравнение движения точки в фазовой плоскости, снабженной комплексной структурой.

При   0 каждая траектория оказывается логарифмической спиралью. Соответствующая картина на плокости P называется фокусом.Если  < 0, то точка при возрастании t асимптотически приближается к началу координат, описывая логарифмическую спираль. Это -устойчивый фокус (рис. 1.11). Если  > 0, то точка уходит от начала координат в бесконечность, и мы имеем неустойчивый фокус (рис. 1.12). Если число  равно нулю, то каждая фазовая траектория, кроме положения равновесия (0,0), замкнута, и мы имеем так называемый центр (рис. 1.13).