1.2 Визначення передаточних функцій системи
Знаходимо передаточну функцію для послідовного з’єднання.
При послідовному з’єднанні ланок вихідна величина кожної попередньої ланки подається на вхід наступної ланки, і тому рівняння динаміки групи послідовно з’єднаних ланок повинно дати залежність вихідної останньої ланки до вхідної величина вхідної величини першої ланки:
2. Знаходимо передаточну функцію зі зворотнім зв’язком
Зворотній зв’язок – це таке виконання зв’язків у системі, при якому на вхід елементу надходить величина пропорційна вихідній величині елементу. Зворотній зв’язок містить у замкнутій системі автоматичного керування (рис. 1.1) і забезпечує надходження на вхід сигналу, пропорційного вихідній величині об’єкту.
Передаточна функція замкнутої системи, у випадку, коли розглядається головний зворотній зв’язок системи автоматичного керування і ланки зворотного зв’язку, дорівнює:
де
;
(див.
розділ 1, п.2.1.2)
Підставивши
відповідні значення отримаємо:
=
Знаходимо передаточну функцію по збуренню
Враховуючи дію збурення F(p) на об’єкт регулювання, передаточна функція системи по збуренню дорівнює:
Розділ 2. Побудова амплітудно-частотних і фазових характеристик системи
2.1 Побудова амплітудно-частотних і фазово-частотних характеристик ланок системи
Амплітудно-частотна
характеристика
має певну
резонансну частоту і спадає при збільшенні
частоти. Діапазон частот, в якому величина
вихідного сигналу перевищує певну малу
величину, прийняту умовно, наприклад
0,05, називають діапазоном пропускання,
а частоту, на якій закінчується діапазон
пропускання, граничною частотою
.
Фазово-частотна характеристика показує, що зі збільшенням частоти зсув фази зростає і досягає певного максимального значення .
Для побудови
амплітудно-частотних та фазово-частотних
характеристик ланок системи будемо
проводити заміну
p=
в передаточну функцію, причому
,
– частота,
і тоді вона
набуватиме вигляду:
Після здійснення відповідної заміни знаходимо дійсну та уявну частини:
–
дійсна частина,
– уявна частина.
Амплітудно-частотна характеристика знаходиться за формулою:
.
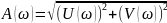Відповідно фазово-частотна характеристика знаходиться:
.
На основі одержаних результатів обчислень будуються графіки, а саме:
амплітудної характеристики;
фазової характеристики;
графік у комплексній площині (залежність
)
Безінерційні ланки
Здійснимо
побудову амплітудно-частотних
та фазово-частотних
характеристик
системи
для
безінерційних
ланок (ланка 1,
2, 6).
Ряд обчислень проведемо на прикладі
ланки 1 -
.
У виразі передаточної функції робимо
заміну
,
вираз набуває вигляду:
Дійсна і уявна частини передаточної функції мають вигляд:
;
Амплітудно-частотна характеристика записується у вигляді:
Фазово-частотна характеристика:
Для побудови графіків будемо користуватись математичним пакетом MathCAD.
Амплітудно-фазова характеристика є прямою, що лежить на дійсній осі комплексної площини (рис.2.1):
а) б)
Рисунок 2.1 - Амплітудно-частотна а) та фазово-частотна б) характеристики безінерційної ланки 1
Аперіодичні ланки першого порядку
Здійснимо побудову амплітудно-частотних та фазово-частотних характеристик системи для аперіодичних ланок першого порядку (ланка 3, 4, 5). Ряд обчислень проведемо на прикладі ланки 3, для ланок 4, 5 алгоритм обчислень буде однаковий.
У вираз
відповідної передаточної функції
робимо заміну p=
,
причому
,
тоді вона набуватиме вигляду:
Ліквідуючи ірраціональність у знаменнику, дістанемо:
Дійсна і уявна частини передаточної функції мають вигляд:
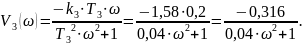
Амплітудно-частотна характеристика записується у вигляді:
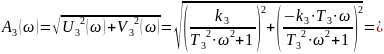
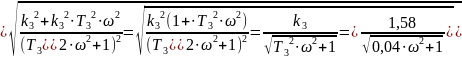
Фазочастотна характеристика:
Задаючи
значення
будуємо амплітудно-частотні характеристики
використовуючи пакет
Mathcad
(рис. 2.2).
а) б)
в) Рисунок 2.2 - Амплітудно-фазові характеристики ланки 3: амплітудно-частотна (а), фазочастотна (б) характеристики та характеристика в комплексній площині (в) аперіодичної ланки першого порядку
Інтегруюча ланка
Здійснимо побудову амплітудно-частотних та фазово-частотних характеристик системи для інтегруючих ланок (ланка 7, 8). Ряд обчислень проведемо на прикладі ланки 7, для ланки 8 алгоритм обчислень буде однаковий.
Передаточна функція інтегруючої ланки 7:
У вираз відповідної передаточної функції робимо заміну p= , причому , тоді вона набуватиме вигляду
Дійсна і уявна частини після перетворення в комплексний вигляд передаточної функції мають вигляд:
Амплітудно-частотна характеристика записується у вигляді:
Фазочастотна характеристика:
Оскільки ,то фазочастотна характеристика
.
На основі отриманих результатів будуємо графіки використовуючи пакет Mathcad (рис. 2.3).
а) б)
Рисунок 2.3 - Амплітудно-частотні характеристики ланки 7: а) амплітудно-частотна характеристика; б) фазочастотна характеристика.