4.2. Аналитическая оценка максимальных коммутационных перенапряжений
Максимальное коммутационное перенапряжение приблизительно рассчитывается как суперпозиция вынужденной и свободной компонент напряжения:
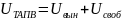
Вынужденная составляющая напряжения максимальна в конце ВЛ:
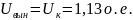
Напряжение свободной составляющей приблизительно определяется модулем разности мгновенных значений напряжений в момент коммутации (tвкл):
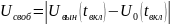
Остаточное напряжение (U0) изменяется по экспоненциальному закону и полагается противоположным по знаку вынужденному (мгновенному) напряжению:
При этом максимальное значение свободной составляющей:
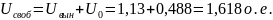
Тогда максимальные коммутационные перенапряжения в цикле ТАПВ:
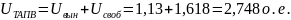
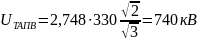
4.3. Расчёт перенапряжений при тапв
Для определения надёжностных характеристик изоляции ЛЭП выполняется расчет максимальных перенапряжений при различных углах включения линейных выключателей.
Рис.4.1. – Упрощённая расчётная схема для анализа перенапряжений при ТАПВ
Расчет коммутационных неограниченных и ограниченных перенапряжений выполняется по упрощенной модели ЛЭП, представленной на рис. 4.1. В качестве базового средства защиты изоляции ВЛ (и оборудования линейной ячейки) от коммутационных перенапряжений на линиях высших классов напряжения выступают оксидно-цинковые нелинейные ограничители перенапряжений (ОПН).
Для расчета используется бесплатно распространяемая программа моделирования стационарных режимов и переходных электромагнитных процессов LTspiceIV. Упрощенная расчетная модель ЛЭП в показана на рис. 4.1.
Расчётная схема в программной среде LTspiceIV приведена на рис. 4.2.
Исходные данные для выполнения расчетов:
Наибольшее рабочее напряжение сети для ВЛ 330 кВ
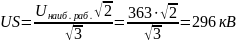
Длина ВЛ LEN=350км
Активное сопротивление ВЛ RL=R1lВЛ=0,03∙350=10,5 Ом
Волновое сопротивление ВЛ по прямой последовательности ZC=305,45 Ом
Индуктивность примыкающей системы
Активное сопротивление примыкающей системы
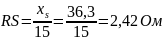
Угол включения э.д.с. φ є [0;170˚] (∆φ=10˚)
Остающееся напряжение ОПН при токе 1А UOPN=0,8US=416 кВ
Дифференциальное сопротивление ОПН
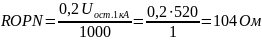
Остающееся напряжение на линии U0, о.е. 1 о.е.=US
Рис. 4.2. схема для моделирования переходного процесса при ТАПВ
Перенапряжения при отсутствии ОПН:
Рис. 4.3. зависимость максимальных неограниченных перенапряжений на ВЛ при различных фазах включения.
Выполним защиту линейной изоляции с помощью ОПНов, расположенных с противоположных сторон ВЛ.
Зависимости ограниченных перенапряжений на ВЛ при установке ОПНов:
Рис 4.4 – Зависимость максимальных ограниченных перенапряжений на ВЛ при разных фазах включения
Зависимости токов, протекающих через ОПН в цикле ТАПВ при различных фазах включения:
Рис. 4.5 – Зависимость максимальных токов, протекающих через ОПН в конце ВЛ, расчет выполнен в именованных единицах.
4.4 Оценка вероятности перекрытия линейной изоляции
Вероятность перекрытия линейной изоляции определяется кратностью максимальных перенапряжений вдоль всей ВЛ. Для учета распределенности максимальных перенапряжений вдоль линии используется их статические характеристики, рассчитанные для начала, середины и конца линии.
Каждый из равных по длине участков разбиения ВЛ содержит следующее кол-во опор:
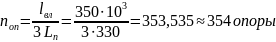
На каждой опоре число изоляционных промежутков провод-траверса равно трем, в то время как число промежутков провод – стойка опоры в отклоненном под воздействием ветрового напора состоянии двум. Это обусловлено тем, что для одной из гирлянд, отклоненной в направлении ветрового потока, перекрытие с провода на стойку опоры маловероятно.
В связи с этим число изоляционных промежутков каждого типа на одном участке разбиения равно:
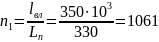
Вероятность перекрытия единичного изоляционного промежутка на участке разбиения линии определится по выражению:
Где
–функция
Лапласа (интеграл вероятности)
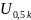– пятидесятипроцентное
разрядное напряжение промежутка k-го
типа при коммутационных перенапряжениях
– оценка
среднеквадратического отклонения
разрядного напряжения для промежутков
типа k.
Для промежутка провод-траверса принимаем
,
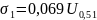провод стойка опоры
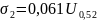
Определим для 2 типов изоляционных промежутков, для 2 крайних фаз А и С:
Импульсное разрядное напряжение гирлянды при коммутационном перенапряжении, промежуток «провод-траверса»:
Где а=305, b= 406, c=-15,2 [3, с.15 табл 4.1]
– расстояние
между проводом фазы А и С и опорой
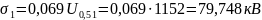
Импульсное разрядное напряжение гирлянды при коммутационных перенапряжениях, промежуток «провод-опора»:
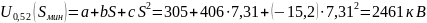
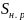– расстояние
между проводом и опорой
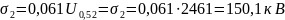
Определим для 2 типов изоляционных промежутков, для верхней фазы B:
Импульсное разрядное напряжение гирлянды при коммутационных перенапряжениях, промежуток «провод-траверса»
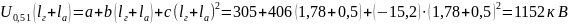
Где а=305, b= 406, c=-15,2 [3, с.15 табл 4.1]
– расстояние между проводом фазы А и С и опорой
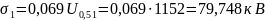
Импульсное разрядное напряжение гирлянды при отрицательной полярности импульса, промежуток «провод-опора»:
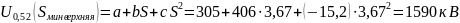
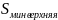– расстояние
между проводом фазы В и опорой
Вероятность перекрытия всей изоляционной системы K-го типа на i-ом участке разбиения линии:
Итоговая вероятность перекрытия изоляции ВЛ под воздействием коммутационных перенапряжений определится как среднее значение из 3-х коммутаций:
