
Елементи лінійної та векторної алгебри
1.Вираз
![]() ,називається:
,називається:
а) визначником (детермінантом) другого порядку; + б) визначником третього порядку;
в) першого порядку; г) інша відповідь.
2.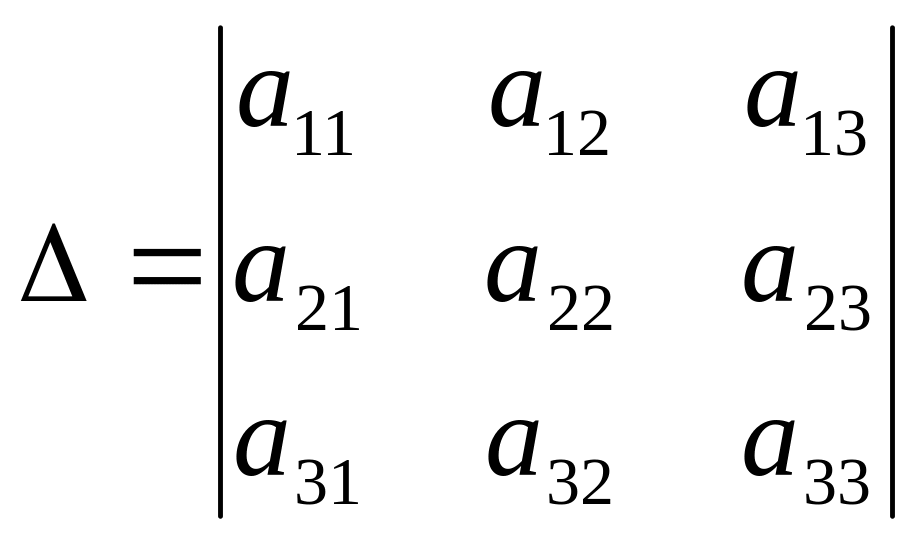 називається
визначником:
називається
визначником:
а) другого; б) третього; + в) n-го порядку; г) інша відповідь.
3.Для обчислення
визначника другого порядку
![]() потрібно:
потрібно:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
+
г) інша
відповідь.
;
+
г) інша
відповідь.
4.Визначники третього порядку обчислюються:
а) за правилом трикутників і методом розкладу визначника за елементами рядка(стовпця); +
б) тільки за правилом трикутників; в) тільки шляхом розкладу визначника за елементами рядка;
г) інша відповідь.
5.Якщо рядки визначника замінити відповідними стовпцями, то:
а) визначник змінюється; б) визначник не змінюється; + в) дорівнює нулю; г) інша відповідь.
6.Якщо переставити місцями два рядки (стовпці), то визначник:
а) не зміниться; б) дорівнює 1; в) змінить знак на протилежний; + г) інша відповідь.
7.Якщо
 ,
то визначник дорівнює:
,
то визначник дорівнює:
а) нулю; +
б)
![]() ;
в) 1;
г) інша
відповідь.
;
в) 1;
г) інша
відповідь.
8.Якщо визначник
 ,
то він дорівнює:
,
то він дорівнює:
а) 1; б) 0; + в) abc;
г) інша відповідь.
9.Якщо у визначнику елементи двох рядків(стовпців) пропорційні, то визначник дорівнює:
а)
![]() ;
б) 1;
в) 0; +
г) інша
відповідь.
;
б) 1;
в) 0; +
г) інша
відповідь.
10.Якщо до елементів одного рядка(стовпця) додати відповідні елементи іншого рядка(стовпця),
помножені на одне й те саме число, то визначник:
а) не зміниться; + б) змінить своє значення; в) поміняє знак; г) інша відповідь.
11.Визначник, який утворюється з даного визначника в результаті викреслення і-го рядка та j-го стовпця, називається:
а) алгебраїчним доповненням; б) мінором Mij; + в) розкладом визначника по елементах рядка(стовпця);
г) інша відповідь.
12.Мінор, взятий зі
знаком
![]() ,
називається:
,
називається:
а) визначником;
б)
Mij;
в)
алгебраїчним доповненням![]() елемента
елемента
![]() ;
+
г) інша
відповідь.
;
+
г) інша
відповідь.
13.Визначник Δ дорівнює:
а)
![]() ;
+
б)
;
+
б)
![]() ;
в)
;
в)
![]() ;
;
г) інша відповідь.
14.Запис визначника
за формулою
![]() називається:
називається:
а) розкладом визначника за елементами будь-якого рядка(стовпця);
б) розкладом визначника за елементами третього рядка; +
в) розкладом визначника за елементами третього стовпчика ; г) інша відповідь.
15.
![]() дорівнює:
дорівнює:
а) 2; б)10; в) -2;+ г) інша відповідь.
16.
![]() =:
=:
а) 1; + б)
![]() ;
в) 0; г) інша відповідь.
;
в) 0; г) інша відповідь.
17. Прямокутна
таблиця чисел
![]() складена
з m
рядків і n
стовпців називається:
складена
з m
рядків і n
стовпців називається:
а) матрицею; + б) визначником; в) детермінантом; г) інша відповідь.
18. Якщо в матриці
![]() то
матриця називається:
то
матриця називається:
а) прямокутною; б) квадратною; + в) діагональною; г) інша відповідь.
19. Матриця, у якої всього один рядок, називається:
а) одиничною матрицею; б) матрицею-стовпцем; в) матрицею-рядком; + г) інша відповідь.
20. Матриця, у якої всього один стовпець, називається:
а) матрицею-стовпцем; + б) одиничною матрицею; в) матрицею-рядком; г) інша відповідь.
21. Дві матриці
![]() та
та
![]() називаються
рівними, якщо:
називаються
рівними, якщо:
а) вони різних
розмірів і
![]() ;
б) вони однакових розмірів і
;
+
;
б) вони однакових розмірів і
;
+
в) вони однакових
розмірів і
![]() ;
г) інша відповідь.
;
г) інша відповідь.
22.Матриця називається нульовою, якщо:
а) всі
![]() ;
б) елементи головної діагоналі рівні
нулю; в) всі її елементи дорівнюють
нулю; + г) інша відповідь.
;
б) елементи головної діагоналі рівні
нулю; в) всі її елементи дорівнюють
нулю; + г) інша відповідь.
23.Якщо всі елементи квадратної матриці , крім тих, що знаходяться на головній діагоналі, дорівнюють нулю, то така матриця називається:
а) діагональною; + б) одиничною; в) нульовою; г) інша відповідь.
24.Матриця
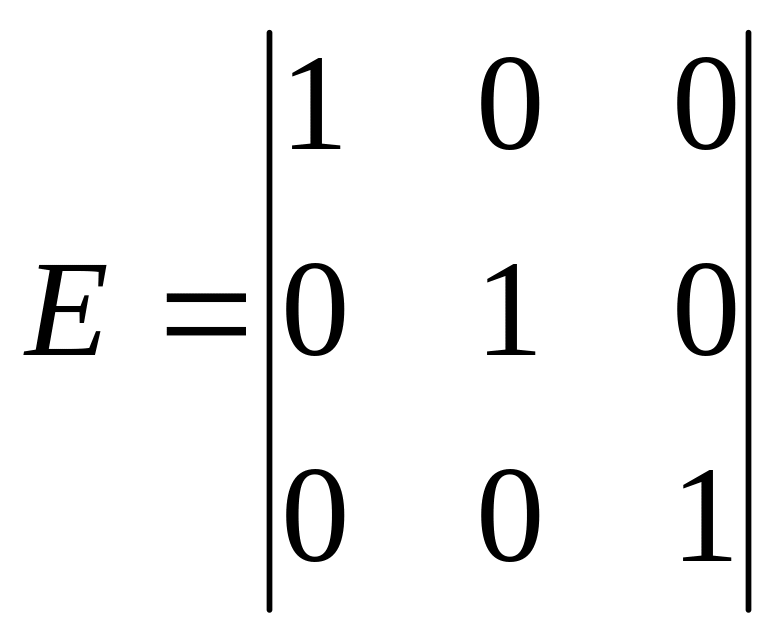 називається:
називається:
а) нульовою; б) одиничною; + в) прямокутною; г) інша відповідь.
25.Операція додавання матриць вводиться тільки для матриць:
а) розміру
![]() ,
якщо
,
якщо
![]() ;
б) розміру
,
якщо
;
б) розміру
,
якщо
![]() ;
в) однакового розміру; + г) інша
відповідь.
;
в) однакового розміру; + г) інша
відповідь.
26.Матриця А називається узгодженою з матрицею В, якщо:
а) кількість стовпців матриці А дорівнює кількості рядків матриці В; +
б) кількість рядків матриці А дорівнює кількості стовпців матриці В;
в) кількість стовпців матриці А дорівнює кількості стовпців матриці В; г) інша відповідь.
27.Добуток
![]() матриць
на
матриць
на
![]() знаходять
за правилом:
знаходять
за правилом:
а) Сарруса; б) множення рядка на стовбець; + в) множення стовпця на рядок; г) інша відповідь.
28.Нехай А- квадратна
матриця. Матриця
![]() називається
оберненою до А, якщо виконується умова:
називається
оберненою до А, якщо виконується умова:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
+ г) інша відповідь.
;
+ г) інша відповідь.
29.Квадратна матриця А називається виродженою, якщо:
а)
![]() ;
+ б)
;
+ б)
![]() ;
в)
;
в)
![]() ;
г) інша відповідь.
;
г) інша відповідь.
30.Квадратна матриця А називається невиродженою, якщо:
а) ; б) ; + в) ; г) інша відповідь.
31.Для існування оберненої матриці необхідно і достатньо, щоб матриця А була:
а) одиничною; б) виродженою; в) не виродженою; + г) інша відповідь.
32.
![]() …:
…:
а)
![]() ;
б)
;
б)
![]() ;
+ в)
;
+ в)
![]() ;
г) інша відповідь.
;
г) інша відповідь.
33.
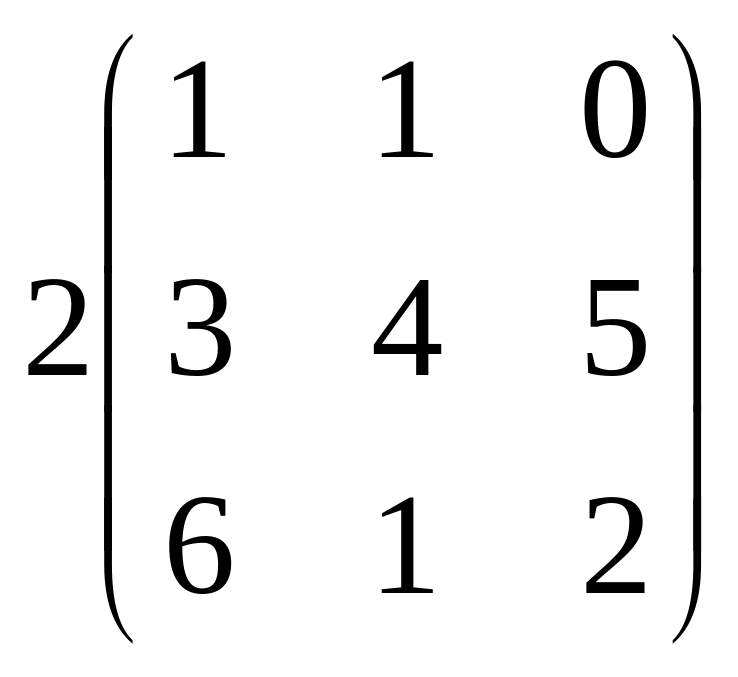 =…:
=…:
а)
 ;
б)
;
б)
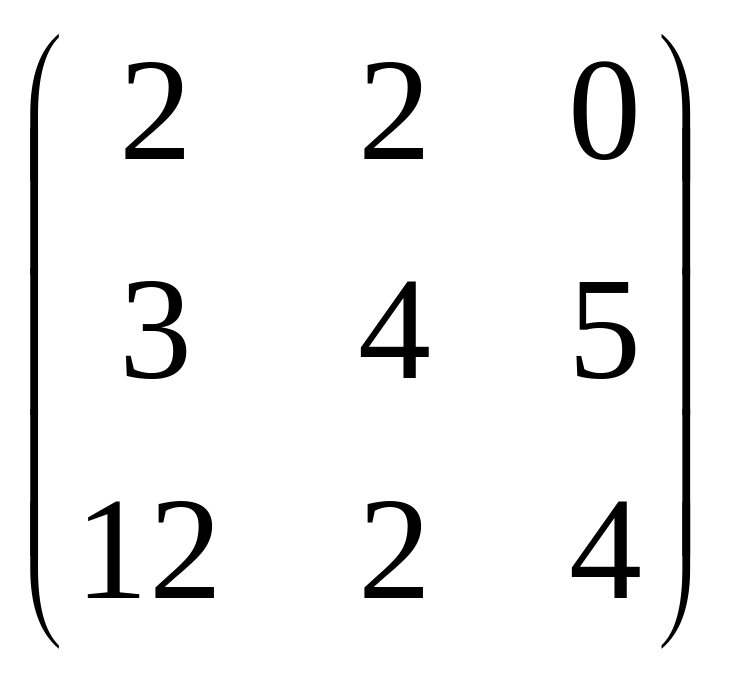 ;
в)
;
в)
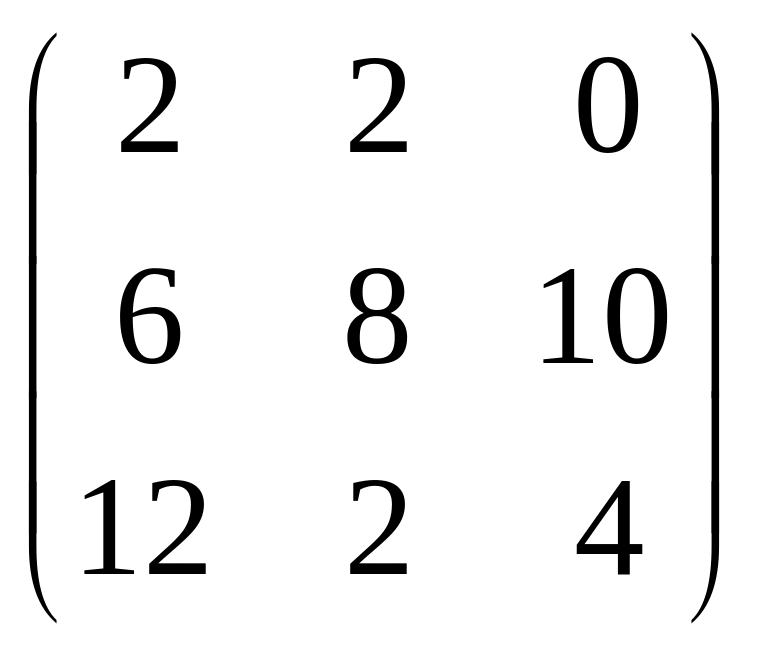 ;
+ г) інша відповідь.
;
+ г) інша відповідь.
34.Формули
![]() називаються:
називаються:
а) формулами Крамера; + б) Гауса; в) Кронекера-Капеллі; г) інша відповідь.
35.Розв’язок системи рівнянь у матричній формі має вид:
а)
![]() ;
б)
;
б)
![]() ;
+ в)
;
+ в)
![]() ;
г) інша відповідь.
;
г) інша відповідь.
36.Метод послідовного виключення невідомих в системі лінійних рівнянь називається:
а) методом Крамера; б) матричним методом; в) методом Гауса; + г) інша відповідь.
37.Фізичні величини, які визначаються своїм числовим значенням, називаються:
а) векторними; б) векторно-скалярними; в) скалярними; + г) інша відповідь.
38.Величини, які крім числового значення мають і напрям, називаються:
а) векторними; + б) скалярними; в) скалярно-векторними; г) інша відповідь.
39.Одиничним вектором називається вектор, довжина якого дорівнює:
а) 0; б) 1; + в) 2; г) інша відповідь.
40.Нульовий вектор визначається:
а) довжиною; б) напрямом; в) немає ні довжини, ні напряму; + г) інша відповідь.
41.Число
![]() називається:
називається:
а) мішаним добутком;
б) векторним добутком; в) скалярним
добутком двох векторів![]() ;
+ г) інша відповідь.
;
+ г) інша відповідь.
42.Якщо добуток двох векторів, заданих координатами в прямокутній системі координат, дорівнює сумі добутків їх відповідних координат, то це:
а) векторний добуток; б) скалярний добуток; + в) мішаний добуток; г) інша відповідь.
43.
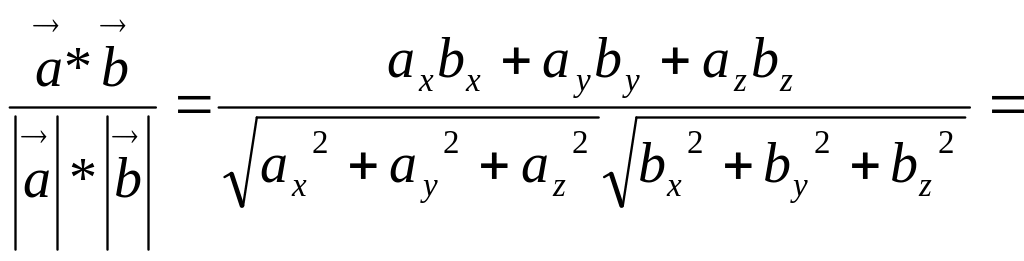
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
+ г) інша відповідь.
;
+ г) інша відповідь.
44.Нехай
![]() і
і
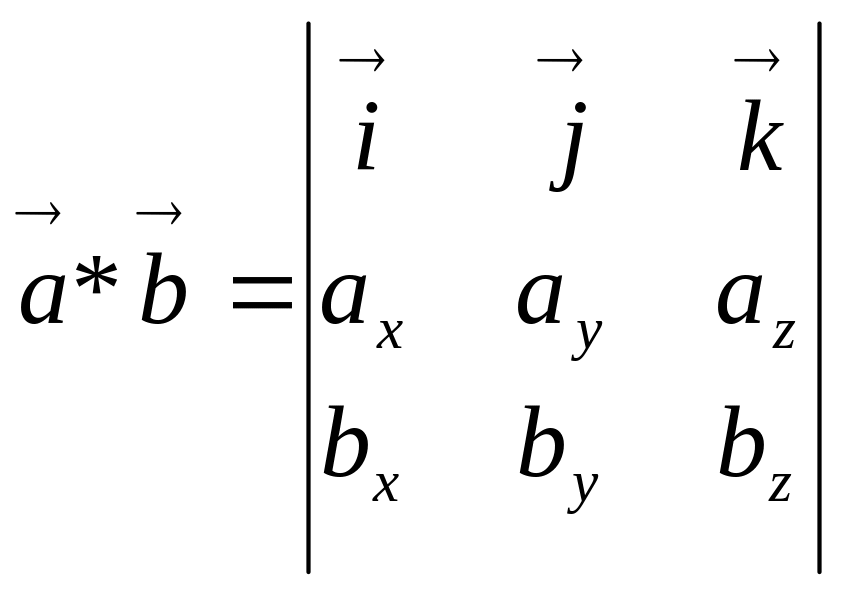 ,
то це:
,
то це:
а) скалярний добуток; б) мішаний добуток; в) векторний добуток; + г) інша відповідь.
45.Скалярний добуток
вектора
![]() на вектор
на вектор
![]() називається:
називається:
а) мішаним добутком; + б) скалярним; в) векторним; г) інша відповідь.
46.Скалярний добуток
двох ненульових векторів
![]() дорівнює:
дорівнює:
а) -13; б) 12; в) 13; + г) інша відповідь.
47.Визначник другого порядку обчислюється за формулою:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
+ г) в)
;
в)
;
+ г) в)
![]() .
.
48.
![]() :
:
а) 17; б) -47; + в) 28; г) -17.
49.
![]() :
:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
+
.
+
50.
![]() :
:
а) 7; б) 13; в) -13; + г) -7.
51.Визначник третього порядку обчислюється за правилом…:
а) правильного трикутника; б) трикутника; + в) чотирикутника; г) інша відповідь.
52.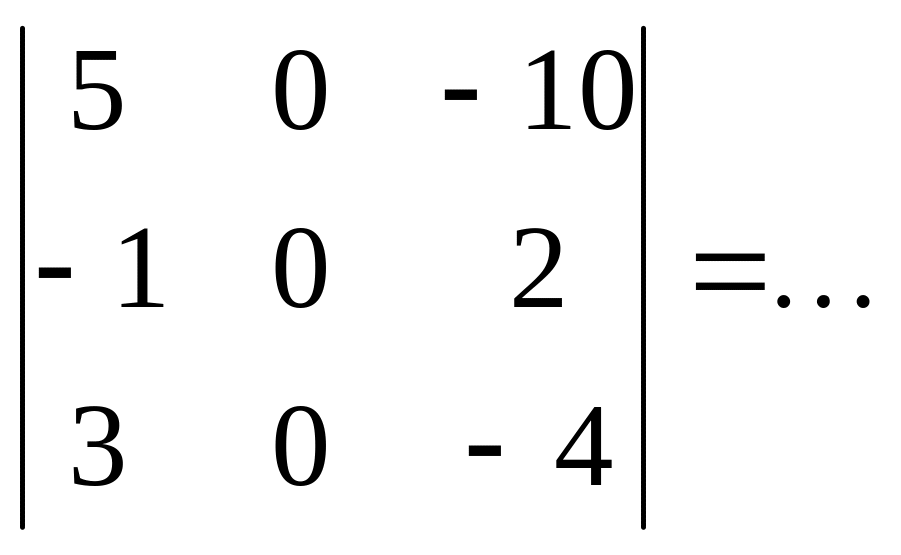 :
:
а) 2; б) -1; в) 1; г) 0. +
53.Обчислити:
 :
:
а) 0; б) -10; + в) 8; г) 10.
54.
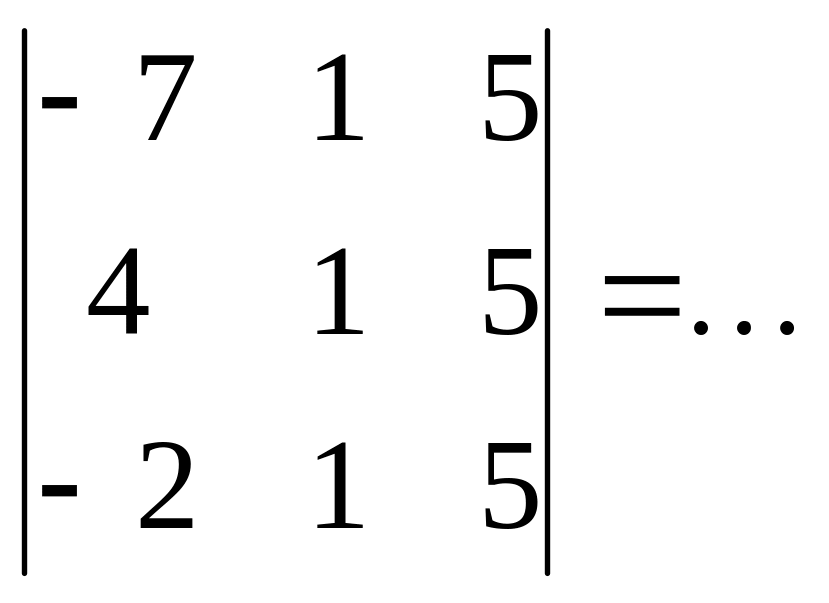 :
:
а) 4; б) 0; + в) -5; г) -2.
55.Алгебраїчне
доповнення
елемента
визначника
![]() рівне:
рівне:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
+ г)
;
+ г)
![]() .
.
56.Для визначника
![]() алгебраїчне
доповнення
алгебраїчне
доповнення
![]() :
:
а) 3; б) -3; + в) -47; г) -7.
57.Матриця
![]() називається:
називається:
а) симетричною; б) квадратною;+ в) правильною; г) прямокутною.
58.Матриця
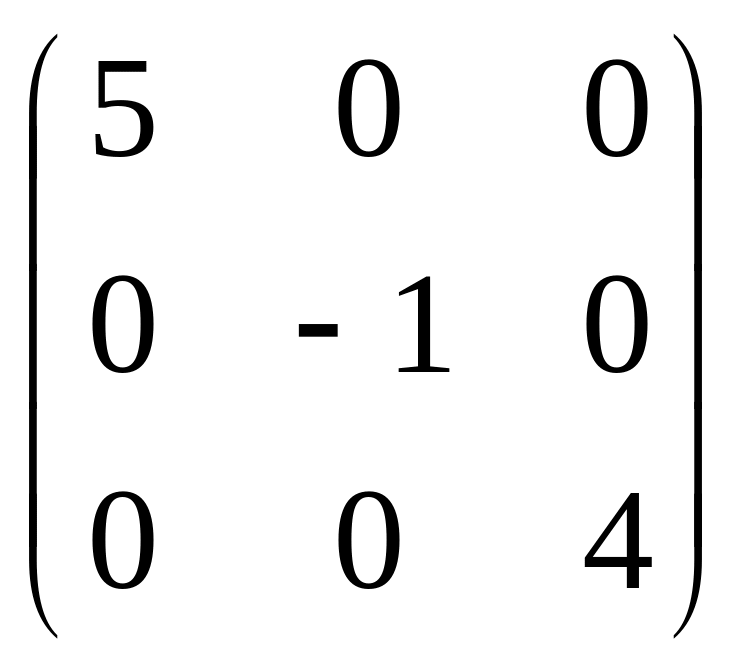 називається:
називається:
а) симетричною; б) головною; в) діагональною; + г) скалярною.
59.Матриця,
транспонована до
![]() ,
рівна:
,
рівна:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .+
.+
60.Транспонованою до матриці-рядка є:
а) симетрична матриця; б) матриця-стовпець; + в) одинична матриця; г) інша відповідь.
61.
![]() :
:
а)
![]() ;
б)
;
б)
![]() ;
+ в)
;
+ в)
![]() ;
г) інша відповідь.
;
г) інша відповідь.
62.
![]() :
:
а) 1; б) -1; в) 2; г) 0. +
63.Якщо![]() ,
то матриця
називається
…:
,
то матриця
називається
…:
а) оберненою до А; + б) симетричною до А; в) транспонованою до А; г) інша відповідь.
64.Якщо матриця А не вироджена, то вона має …:
а) симетричну; б) транспоновану; в) обернену; + г)інша відповідь.
65.Матриця А є невиродженою, якщо її …:
а)
![]() ;
б)
;
б)
![]() ;
+ в)
;
+ в)
![]() ;
г)
;
г)
![]() .
.
66.Якщо у методі
Крамера
![]() ,
то система має …:
,
то система має …:
а) нескінченну кількість розв’язків; б) єдиний розв’язок; + в) всі корені нулі; г) немає жодного розв’язку.
67.Формула
![]() називається
… записом розв’язку
системи рівнянь:
називається
… записом розв’язку
системи рівнянь:
а) скороченим; б) еквівалентним; в) матричним; + г) зведеним.
68.Метод Гауса – це метод …:
а) розв’язку матричного рівняння; б) послідовного виключення невідомих; + в) розв’язку системи за формулами;
г) підстановки.
69.Координати
вектора
![]() :
:
а) (-3;2;5); б) (3;-2;5); в) (3;-2;5); г) (-3;2;-5). +
70.![]() :
:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
+
.
+
71.Довжина
![]() :
:
а) 3; + б) 5; в) 1; г) 4.
72.![]() :
:
а) (6;1;3); б) (-4;3;-1); в) (-4;1;-1); г) (4;-3;1). +
73.![]() :
:
а) 2; б) 7; + в) 3; г) 5.
74.
Знайти
координати та модуль вектора
![]() ,
якщо
,
якщо
![]() ,
,
![]() :
:
а)
![]() ;
;
![]() ;
б)
;
б)
![]() ;
;
+ в)
;
;
+ в)
![]() ;
;
![]() ;
г)
;
г)
![]() ;
;
![]() .
.
75. Які вектори називаються колінеарними:
а) які лежать на одній прямій, або на паралельних прямих;+ б) які лежать на одній площині, або на паралельних площинах;в) які лежать на перпендикулярних прямих; г) які лежать на одній прямій.
76. Встановити відповідність між визначником та його значенням:
1.
![]() А) 23 ;
А) 23 ;
2.
![]() Б) -13;
Б) -13;
3.
![]() В) 13;
В) 13;
4.
![]() Г) -23.
Г) -23.
77. Встановити
відповідність між мінором даного
визначника
![]() та його значенням:
та його значенням:
1.
![]() А)
-4;
А)
-4;
2.
![]() Б)
9;
Б)
9;
3.
![]() В)
1;
В)
1;
4.
![]() Г)
5.
Г)
5.
78. Встановити відповідність між алгебраїчним доповненням даного визначника та його значенням:
1.
![]() А)
-4;
А)
-4;
2.
![]() Б)
9;
Б)
9;
3.
![]() В)
-1;
В)
-1;
4.
![]() Г)
-5.
Г)
-5.
