Вопрос 32. Вычисление криволинейного интеграла 2 рода.

1. Пусть кривая альфа задана как график ф-ции y=f(x), x € [a,b]

∫ ( снизу L ) FdS= ∫ ( снизу L )X(x,y)dx+Y(x,y)dy= ∫ ( ot a do b) X(x,f(x)) – Y (x, f(x)) f’(x) dx

2. Если кривая альфа задана параметрически:

x=(t), y= Ψ(t), t €[α,β]

∫ ( снизу L )FdS= ∫ ( ot a do b) X( 𝝋(t), Ψ(t)) * 𝝋’(t) ddt + Y (𝝋(t), Ψ(t)) * Ψ’(t) dt

Вопрос 33. Приложения криволинейных интегралов.

1.  Длина кривой 

 2.    Масса кривой 

(  - плотность кривой).

 3.   Координаты центра масс 

  4.   Работа 

5. Работа силы  вдоль кривой l:

Вопрос 34. Дифференциальные уравнения. Определение, порядок, общее решение, общий интеграл, начальные условия, частные решения, частный интеграл. Теорема о существовании и единственности решения задачи Коши для дифференциального уравнения 1-го порядка.

Опр: уравнение F(x,y,y’,y’’…)=0 называется д.у. n-го порядка

Опр: функция y=𝝋(x) удовлетворяющая д.у, называется решением д.у.

Пр: 3y-x*y’=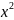 –д.у. первого порядка

y= -решение д.у

Д.у. первого порядка: F(x,y,y’)=0

Решением явл ф-ция y=𝝋(x)

Так для уравнения y=3x^2решением явл ф-ция y= x^3, y=x^3 +3, y=x^3 +C

Решение вида y=𝝋(x,C) называется общим решением д.у. 1-го порядка.

Решение д.у. еще называют интегральной кривой

Условие y(x˳)=y˳ называется начальным условием для д.у. С помощью начального условия из семейства интегральных кривых можно выбрать только одну кривую. Т.е. начальное условие помогает из общего решения выбрать то частное решение, которое удовлетворяет этому начальному условию.

Теорема (О существовании и единственности решения задачи Коши).Пусть   — непрерывная функция в области  , причем   — также непрерывен в  . Тогда для любой точки   Задача Коши:   имеет решение, причем единственное в том смысле, что если есть 2 ее решения   и  , определенные на интервалах   и  , содержащих точку  , то они совпадают на пересечении   этих интервалов.

Замечание. Говорят, что решение   дифференциального уравнения на интервале   есть Продолжение решения   на  , если   и   на  . Также говорят, что решение   —Максимальное или Непродолжаемое относительно  , если   не обладает продолжениями, целиком лежащими в  .

На основании этого замечания можно сказать, что при условиях теоремы существует единственное максимальное (непродолжаемое) решение задачи Коши.

Геометрический смысл сформулированной теоремы состоит в следующем. Левая часть уравнения   представляет собой   — тангенс угла наклона касательной к графику искомой функции в точке  , а правая часть   задает его численное значение   в этой точке. Поэтому можно считать, что уравнение задает Поле направлений на области  , т. е. к каждой точке   прикреплен вектор, указывающий направление касательной к искомой интергальной кривой.

Поэтому сформулированная выше теорема означает, что при выполнении ее условий через каждую точку   проходит единственная непродолжаемая интегральная кривая.

Перейдем к простейшим типам дифференциальных уравнений, для которых можно в явном виде получить их решения.