Вопрос 7. Комплексные числа. Тригонометрическая форма комплексного числа. Действия с комплексными числами. Формула Муавра.

Чтобы возвести к.ч. в степень или извлечь корень нужно перевести число в тригонометрическую форму.

Тригонометрическая форма к.ч.: обозначим |Z|=r= √a^2+b^2и назовем модулем к.ч.

Для перевода числа в тригонометрическую форму выполним след.действия Ƶ= а+iв= r(a+ib)/r= r(a/r+ib/r)= r(cosϕ+isinϕ)-триг.форма к.ч.

Формула Муавра:

Z^n =(r(cosϕ+isinϕ))^n=r^n (cosϕ+isinϕ)^n= r^n(cosnϕ+isinnϕ)

6)извлечение корня из к.ч.

Пусть Ƶ=r(cosϕ+isinϕ)-некоторое к.ч.

√Z(n)= Z^1/n=r^1/n (cos(𝝋+2Пr/n) + isin (𝝋+2Пr/n)

R=0,1,2…,n-1

Вопрос 8. Комплексные числа. Показательная форма комплексного числа. Действия с комплексными числами.

Рассмотрим числа Ƶ1= r1(cos𝝋1+isin𝝋1)

Ƶ2= r2(cos𝝋2+isin𝝋2)

Ƶ1*Ƶ2= r1(cos𝝋1+isin𝝋1)* r2(cos𝝋2+isin𝝋2)=r1*r2*( cos𝝋1* cos𝝋2+ cos𝝋1*isin𝝋2+isin𝝋1* cosϕ2+isin𝝋1*isin𝝋2)= r1*r2(cos𝝋1* cos𝝋2-sin𝝋1*sin𝝋2-i(cos𝝋1*sin𝝋2+sin𝝋1* cos𝝋2))= r1*r2(cos(𝝋1+𝝋2)+i(sin(𝝋1+𝝋2)))

Обозначим cos 𝝋+isin 𝝋=e^i𝝋

Тогда любое число Ƶ можно записать в виде Ƶ=r(cos𝝋+isin𝝋)=r*e^i𝝋

Запись к.ч. Ƶ= r*e^i𝝋 называется показательной формой к.ч.

Тогда Z^n=( r* e^i𝝋 )^n= r^n* e^in𝝋 =r^n (cos n𝝋+isinn𝝋)

Если Ƶ1=r1* e^i𝝋1; Ƶ2=r2* e^i𝝋2, то

Ƶ1*Ƶ2= r1* e^i𝝋1 *r2* e^i𝝋2 =r1*r2* e^i𝝋1+i𝝋2 =r1*r2*e^i(𝝋1+𝝋2)= r1*r2(cos(𝝋1+𝝋2)+isin(𝝋1+𝝋2))

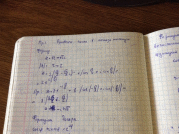
Вопрос 9. Элементарные функции комплексной переменной. Примеры.

Формула Эйлера:

2cos𝝋= e^i𝝋+ e^-i𝝋

cos𝝋= (e^i𝝋+ e^-i𝝋)/2

вычтем теперь эти равенства:

2isin 𝝋= e^i𝝋+ e^-i𝝋

Sin 𝝋= (e^i𝝋+ e^-i𝝋)/2i

Формулы Эйлера используют при вычислении значений тригонометрических функций комплексного переменного

cosƵ= (e^iz+ e^-iz )/2

sinƵ=(e^iz+ e^-iz )/2i

примеры:

Вопрос 10. Производная функции комплексной переменной. Условие Коши-Римана.(?)

Опр. Пусть в области J компл. переменной z задана функция f(z). Если для точки z₀ÎJ, $ при Dz®0 предел разностного отношения ,то этот предел называется производной функции f(z) по комплексной переменной z в точке z₀.  (1) Теор. (Условие Коши-Римана)Если функция f(z) = u(x,y) + i v(x,y) диф-ма в точке z₀ = x₀ + i y₀, то в точке (x₀,y₀) $ частные производные функций u(x,y) и v(x,y) по переменным x, y. Причем ,  (2)

Вопрос 11. Понятие неопределенного интеграла. Свойства неопределенного интеграла.

Опр: выражение f(x)+c называется неопределенным интегралом функции f(x) и обозначается:

∫f(x)dx= F(x)+c

Свойства неопределенных интегралов:

1. ∫(f(x)+g(x))dx= ∫f(x)dx+ ∫g(x)dx

2. ∫c*f(x)dx =c* ∫f(x)dx

3. ∫dx f(x)+c

4. ∫f’(x)dx= ∫df= f(x)+c

5. (∫f(x)dx )’=f(x)

6. f(x)dx=f(x)dx

7. ∫f(rx+b)dx= F(rx+b)/r+c

Вопрос 12. Метод непосредственного интегрирования.

Метод интегрирования, при котором интеграл с помощью тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

Таким образом, алгоритм действий следующий:

1. тождественное преобразование подынтегральной функции;

2. применение свойств неопределенного интеграла: вынесение константы за знак интеграла, представление интеграла от суммы функций в вид суммы интегралов;

3. использование таблицы интегралов.

В простейших примерах для применения непосредственного интегрирования достаточно разложить подынтегральную функцию на слагаемые и постоянные величины вынести за знак интеграла.

При определенной практике интегрирования обычно эти действия проводят устно, записывая лишь результат интегрирования.