Рівняння траєкторного руху

Рівнянння траєкторного руху можна отримати проектуючи вектор швидкості, напрямок якого збігається з напрямком осі X_к траєкторної системи координат, на осі нормальної системи координат (мал. Д.6).

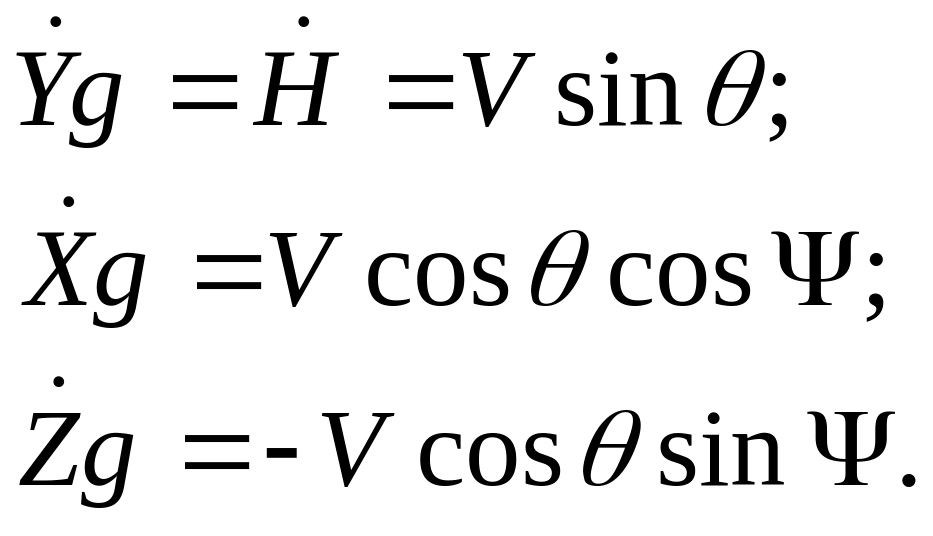(Д.18)

Рівняння, що описує зміну висоти польоту Н, необхідне також для виявлення функціональних залежностей аеродинамічних сил і моментів, а також тяги двигуна від густини повітря, яка змінюється з висотою польоту.

Використовуючи (Д.16) в рівняннях сил, отримаємо замкнену систему рівнянь, що описує просторовий рух літака у вигляді:

(Д.19)

У подальшому, розкриваючи залежність аеродинамічних сил і моментів від параметрів польоту,

,

де

C_ya=C_ya(,V,_в)

C_xa=C_xa(,V)

C_za=C_za(,_н)

m_x= m_x(,_x,_y,_н,_э)

m_y=m_y(,_x,_y,_н,_э)

m_z= m_z(V,, ,_z,_в)

отриману систему рівнянь (Д.19) можна використовувати для аналізу контурів автоматичного управління шляхом моделювання на ЦОМ.

Додаток 2. Вивід лінеарізованих рівнянь на основі повної системи рівнянь ізольованого поздовжнього руху

Для лінеаризації нелінійної системи рівнянь (2.1) необхідно призначити незбурений (програмний) рух. За програмний рух, як правило, обирається режим прямолінійного горизонтального польоту з постійною швидкістю. Незбуреному руху відповідає вихідна система рівнянь при певних початкових умовах:

(Д.20)

Параметри збуреного руху необхідно подати як суму параметрів незбуреного руху та малих відхилень.

(Д.21)

Оскільки похідні від параметрів незбуреного руху (від величин постійних) дорівнюють нулю, то очевідні співвідношення:

Для подання нелінійних залежностей вихідної системи рівнянь у вигляді (Д.21) розкладемо ці функції в ряд Тейлора, обмежуючись тільки лінійними членами розкладання. Частинні похідні, що входять у вирази для ступеневих рядів, визначаються в точці, яка відповідає незбуреному руху. В аеродинаміці прийнято позначати їх з верхнім індексом, що відповідає параметру, від якого береться похідна.

Наприклад: ; .

Розкладання нелінійних залежностей в ряд Тейлора з урахуванням

X_a X_aV, H, 

Y_a Y_aV, H, 

M_z M_zV, H,  ,_z_в 

P PV, H, _p

має вигляд:

(Д.20)

В останіх четирьох рівняннях ураховується, що .

Підставимо отримані вирази у вихідну систему, віднімемо з цих рівнянь рівняння незбуреного руху. Для запису системи диференціальних рівнянь у формі Коши розділимо перше рівняння на m , друге на mV₀ , а третє на J_z .

Після зведення подібних членів отримаємо рівняння поздовжнього руху у малих відхиленнях:

(Д.23)

Коефіцієнти лінеаризованої системи рівнянь мають вигляд:

(Д.24)

Коефіцієнти , , обумовлюють зміни аеродинамічних сил і моментів, а також тяги двигуна при змінах густини повітря з висотою польоту. При малих відхиленнях з висоти H можна знехтувати складовими , , , що тільки спрощує математичну модель, оскільки кінематичне рівняння не впливає на останні рівняння системи , тому вони можуть розглядатись окремо. Крім того, можна нехтувати коефіцієнтом , зважаючи на його малість.

Перетворимо отриману систему рівнянь. Після диференціювання співвідношення та підставлення в нього , можна з урахуванням другого рівняння системи (Д.23) отримати

(Д.25)

Підставляючи у третє рівняння системи (Д.23) і доповнюючи систему співвідношенням (Д.25), отримаємо з урахуванням вище зроблених припущень:

(Д.26)

Коефіцієнти третього рівняння системи перераховуються за формулами:

(Д.27)

У теорії автоматичного керування прийнято записувати математичні моделі в безрозмірній формі, тобто, вводити відносні (безрозмірні) координати. При цьому попередньо необхідно обрати базові значення змінних величин. Наприклад: , де - базове значення перемінної x.

Обираючи за базове значення для кутових параметрів величину в один радіан, а для швидкості польоту величину V₀ , отримаємо:

У подальшому риску над позначенням безрозмірних параметрів будемо пропускати.

Для переходу до безрозмірних координат помножимо та поділимо кожний член, що утримує V та похідну від V на V₀ , а обидві частини першого рівнянння поділимо на V₀. Внаслідок отримаємо:

(Д.28)

Коефіцієнти математичної моделі (Д.28), з урахуванням (Д.24), (Д.27) та співвідношень для аеродинамічних сил і моментів (1.12), мають вигляд:

(Д.29)

Тут , похідні з безрозмірних кутових швидкостей

Далі, застосовуючи перетворення Лапласа до системи (Д.28) при нульових початкових умовах, отримаємо математичну модель поздовжнього руху літака в операційній формі:

(Д.30)

При отриманні рівнянь поздовжнього короткоперіодичного руху вважають незалежність цього руху від швидкості польоту. Зауважимо, що для умов програмного горизонтального польоту sin_, а, отже, коефіцієнти ; . Враховуючи ці умови, система рівняь, що описує поздовжній короткоперіодичний рух набуває вигляду:

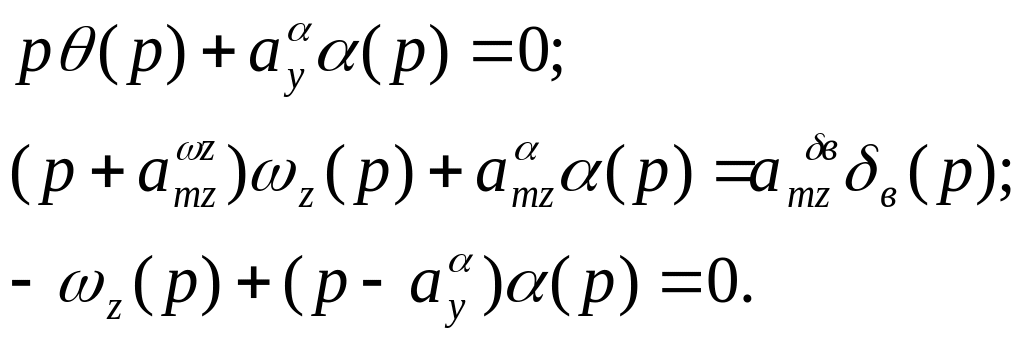(Д.31)

Перше рівняння системи (Д.31) не впливає на інші тому може розглядатись окремо. Системі з двох рівнянь, що залишаються, відповідає характеристичне рівняння.

, (Д.32)

де ;

.

У довгоперіодичному русі кут атаки практично не змінюється, тому можна вважати p , тоді _z p, а кут похилу траєкторії змінюється повільно, отже, припускають p_z p²  0. При таких допущеннях система рівнянь, що описує довгоперіодичний рух набуває вигляду:

(Д.33)

Системі (Д.34) відповідає характеристичне рівняння.

(Д.34)

де ;

;

.

Таким чином, поздовжній рух розпадається на дві складові, які рознесені за часом і частотою, що надає можливість їх роздільного дослідження.