
- •§12.1. Уравнения прямой на плоскости
- •§ 12.2. Взаимное расположение прямых на плоскости
- •§12.3. Расстояние от точки до прямой
- •§ 12.4. Полярные координаты
- •§ 12.5. Окружность
- •§ 12.6. Эллипс
- •§ 12.7. Гипербола
- •§ 12.8. Парабола
- •§ 12.9. Полярное уравнение линии второго порядка
- •§ 12.10. Общая теория линий второго порядка
- •Гипербола и её каноническое уравнение
- •Как построить гиперболу?
- •Определение гиперболы. Фокусы и эксцентриситет
- •Равносторонняя гипербола
- •Поворот вокруг центра и параллельный перенос гиперболы
- •Парабола и её каноническое уравнение
- •Определение параболы:
- •Поворот и параллельный перенос параболы
- •Гиперболоид
Определите общую прямую двух пучков
![]()
![]()
§12.3. Расстояние от точки до прямой
Уравнение ![]() называется
уравнением прямой в нормальной
форме,
если
называется
уравнением прямой в нормальной
форме,
если ![]() Общее
уравнение прямой приводится к нормальному
виду с помощью нормирующего
множителя
Общее
уравнение прямой приводится к нормальному
виду с помощью нормирующего
множителя![]() где
принято знак выбирать противоположным
свободному члену, т. е.
где
принято знак выбирать противоположным
свободному члену, т. е. ![]()
Пусть
точка ![]() лежит
на расстоянии
лежит
на расстоянии ![]() от
прямой и
-
проекция точки на эту прямую,
-
нормаль к прямой. Для нормального
уравнения длина вектора нормали равна
1. Отклонением
точки
от
прямой называется
число
от
прямой и
-
проекция точки на эту прямую,
-
нормаль к прямой. Для нормального
уравнения длина вектора нормали равна
1. Отклонением
точки
от
прямой называется
число ![]() ,
равное
,
если векторы
и
,
равное
,
если векторы
и ![]() со
направлены и
со
направлены и ![]() ,
если
и
противоположно
направлены. Тогда
,
если
и
противоположно
направлены. Тогда![]()
Так
как ![]() то
то![]()
![]() Для
общего уравнения расстояние от точки
до
плоскости вычисляется по формуле
Для
общего уравнения расстояние от точки
до
плоскости вычисляется по формуле
Нормальное
уравнение часто записывают в
виде ![]() Здесь
Здесь ![]() ,
, ![]() -
направляющие косинусы вектора нормали.
Геометрический смысл параметра
-
направляющие косинусы вектора нормали.
Геометрический смысл параметра ![]() -
расстояние от начала координат до
плоскости. Вектор нормали направлен в
сторону полуплоскости, в которой нет
начала координат.
-
расстояние от начала координат до
плоскости. Вектор нормали направлен в
сторону полуплоскости, в которой нет
начала координат.
Геометрический
смысл знака трехчлена![]() :
для того, чтобы точка
и
вектор
лежали
в одной полуплоскости относительно
прямой
необходимо
и достаточно, чтобы выполнялось условие
:
для того, чтобы точка
и
вектор
лежали
в одной полуплоскости относительно
прямой
необходимо
и достаточно, чтобы выполнялось условие ![]()
Задача.
Даны точки ![]() и
и ![]() и
прямая
и
прямая ![]() Проходит
ли прямая через внутреннюю точку
отрезка
Проходит
ли прямая через внутреннюю точку
отрезка ![]()
Так
как числа![]() и
и![]() имеют
разные знаки, то точки принадлежат
различным полуплоскостям относительно
прямой.
имеют
разные знаки, то точки принадлежат
различным полуплоскостям относительно
прямой.
прямая пересекает отрезок.
Упражнения
Какие стороны треугольника с вершинами


 пересекаются
каждой из осей координат?
пересекаются
каждой из осей координат?Докажите, что четырехугольник с вершинами



 выпуклый.
выпуклый.Докажите, что четырехугольник с вершинами



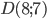 невыпуклый.
невыпуклый.Дан четырехугольник



а) Докажите, что точки
 и
и  лежат
внутри данного четырехугольника.
лежат
внутри данного четырехугольника.б) Докажите, что точки
 и
и  лежат
вне данного четырехугольника.
лежат
вне данного четырехугольника.
Даны стороны треугольника


 Составьте
систему неравенств, определяющую
внутреннюю область треугольника.
Составьте
систему неравенств, определяющую
внутреннюю область треугольника.Изобразите на чертеже область, определяемую системой неравенств

Найдите длины высот треугольника, стороны которого заданы уравнениями:
 и
и 
Напишите уравнение окружности с центром в точке
 ,
касающейся прямой
,
касающейся прямой 
Выведите формулу для вычисления расстояния между параллельными прямыми
 и
и  Пользуясь
полученной формулой, определите
расстояние между прямыми
Пользуясь
полученной формулой, определите
расстояние между прямыми  и
и 
Составьте уравнения прямых, отстоящих от прямой
 на
расстоянии, равном 3.
на
расстоянии, равном 3.Составьте уравнение геометрического места точек, равноудаленных от двух параллельных прямых:
а)

б)

На прямой
 найдите
точки, равноудаленные от прямых
найдите
точки, равноудаленные от прямых  и
и 
Составьте уравнение биссектрисы того угла между прямыми
 и
и  в
котором лежит начало координат.
в
котором лежит начало координат.Даны уравнения сторон треугольника:
 и
и  Составьте
уравнения вписанной и вневписанных
окружностей.
Составьте
уравнения вписанной и вневписанных
окружностей.Луч света направлен по прямой
 Дойдя
до прямой
Дойдя
до прямой  луч
отразился. Составьте уравнение прямой,
на которой оказался отраженный луч.
луч
отразился. Составьте уравнение прямой,
на которой оказался отраженный луч.Составьте уравнения сторон треугольника
 зная
уравнения двух биссектрис
зная
уравнения двух биссектрис 
 и
координаты вершины
и
координаты вершины 
§ 12.4. Полярные координаты
Возьмем
на плоскости прямую. Выберем на ней
точку
и
единичный вектор ![]() а
также некоторое положительное направление
обхода. Пусть
-
произвольная точка плоскости, отличная
от
а
также некоторое положительное направление
обхода. Пусть
-
произвольная точка плоскости, отличная
от ![]() Положение
этой точки однозначно определено
заданием длины
Положение
этой точки однозначно определено
заданием длины ![]() отрезка
и
углом
между
векторами
отрезка
и
углом
между
векторами ![]() и
и ![]() Числа
и
называются полярными
координатами точки
При
этом
называется
полярным
радиусом,
а
- полярным
углом.
Если
имеет
полярные координаты
и
Числа
и
называются полярными
координатами точки
При
этом
называется
полярным
радиусом,
а
- полярным
углом.
Если
имеет
полярные координаты
и ![]() то
пишем
то
пишем ![]() Точка
называется полюсом,
а луч
Точка
называется полюсом,
а луч ![]() - полярной
осью.
Точка
- полярной
осью.
Точка ![]() вектор
и
положительное направление обхода
плоскости образуют полярную
систему координат.
вектор
и
положительное направление обхода
плоскости образуют полярную
систему координат.
Заметим,
что полярный угол имеет бесконечное
много значений. Если
совпадает
с
то ![]() а
значение
считаем
неопределенным.
а
значение
считаем
неопределенным.
Пусть ![]() -
прямоугольная декартова система, где
вектор
-
прямоугольная декартова система, где
вектор ![]() получен
из вектора
и
поворотом на 90
получен
из вектора
и
поворотом на 90![]() Полярные
и прямоугольные декартовы координаты
точки
связаны
соотношениями Иногда рассматривают обобщенные
полярные координаты.
В этом случае считаем, что полярный
радиус может принимать и отрицательные
значения. Например, точка с полярными
координатами (3; 210
Полярные
и прямоугольные декартовы координаты
точки
связаны
соотношениями Иногда рассматривают обобщенные
полярные координаты.
В этом случае считаем, что полярный
радиус может принимать и отрицательные
значения. Например, точка с полярными
координатами (3; 210![]() )
имеет обобщенные полярные координаты
(-3; 30
).
)
имеет обобщенные полярные координаты
(-3; 30
).
Найдем
полярное уравнение прямой на плоскости.
Пусть прямая задана нормальным
уравнением
Выразив
переменные через полярные координаты,
получим![]() или
или![]() Это
и есть полярное уравнение прямой на
плоскости.
Это
и есть полярное уравнение прямой на
плоскости.
Упражнения
В полярной системе координат даны точки
 и
и  Вычислите
расстояние между ними.
Вычислите
расстояние между ними.Вычислите площадь треугольника
 если
-
полюс и известны полярные координаты
вершин
если
-
полюс и известны полярные координаты
вершин 
Треугольник задан полярными координатами вершин:


 Докажите,
что треугольник равнобедренный.
Докажите,
что треугольник равнобедренный.Треугольник задан полярными координатами вершин:


 Докажите,
что треугольник прямоугольный.
Докажите,
что треугольник прямоугольный.Как расположены точки на плоскости, полярные координаты которых удовлетворяют одному из условий: а)
 б)
б)  в)
в) г)
г)  д)
д) е)
е)
§ 12.5. Окружность
Окружностью называется геометрическое место точек плоскости, равноудаленных от данной точки. Данная точка называется центром окружности. Расстояние любой точки окружности до центра называется радиусом окружности.
Пусть ![]() -
центр окружности,
-
ее радиус, а
-
центр окружности,
-
ее радиус, а![]() )
- текущая точка окружности. Тогда
)
- текущая точка окружности. Тогда![]() Возведя
обе части равенства в квадрат, получим
нормальное уравнение окружности
Возведя
обе части равенства в квадрат, получим
нормальное уравнение окружности![]() Если
центр окружности совпадает с началом
координат, то имеем каноническое
уравнение окружности
Если
центр окружности совпадает с началом
координат, то имеем каноническое
уравнение окружности![]()
r:
OK
Пример.
Найдите координаты центра и радиус
окружности![]()
Выделив
полные квадраты, преобразуем уравнение
к виду![]() или
или![]()
![]()
Упражнения
Если точка лежит вне окружности
 то
то  а
если внутри окружности, то
а
если внутри окружности, то  Докажите
это.
Докажите
это.Найдите геометрическое место точек плоскости, отношение расстояний которых от двух данных точек и этой плоскости постоянно и равно

Найдите геометрическое место точек плоскости, сумма квадратов расстояний которых от двух данных точек и этой плоскости постоянна.
Найдите геометрическое место точек плоскости, сумма квадратов расстояний которых от трех данных точек
 и
этой
плоскости постоянна.
и
этой
плоскости постоянна.Найдите геометрическое место точек, касательные из которых, проведенные к данной окружности, имеют постоянную длину.
Определите геометрическое место точек плоскости, из которых данный отрезок виден под прямым углом.
Дана окружность радиуса и на ней точка . Найдите геометрическое место точек, делящих всевозможные хорды, проведенные через
 в
одном и том же отношении.
в
одном и том же отношении.Найдите геометрическое место середин всех хорд окружности, имеющих данную длину.
§ 12.6. Эллипс
Эллипсом называется
геометрическое место точек плоскости,
сумма расстояний которых до двух
фиксированных точек этой плоскости,
постоянна. Эти две фиксированные
точки
и
называются
фокусами.
Длина отрезка
называется фокусным
расстоянием.
Постоянную сумму расстояний обозначим
через ![]() так
что для любой точки
эллипса
имеем
так
что для любой точки
эллипса
имеем ![]() Считаем,
что
Считаем,
что ![]()
Эллипс можно построить с помощью нити длиной закрепленной концами в фокусах. Зацепив нить острием карандаша и двигая его так, чтобы нить все время была в натянутом состоянии, мы острием карандаша вычертим эллипс.
Для
изучения эллипса применим метод
координат, который в данном случае
заключается в выборе системы координат,
в которой уравнение эллипса имеет
наиболее простой вид и наиболее удобный
для исследования. За ось абсцисс примем
прямую, проходящую через фокусы, а
серединный перпендикуляр отрезка
за
ось ординат. Тогда координаты
фокусов
и ![]() Точка
принадлежит
эллипсу тогда и только тогда, когда
Точка
принадлежит
эллипсу тогда и только тогда, когда![]() Получили
уравнение эллипса. Преобразуем его.
Получили
уравнение эллипса. Преобразуем его.![]()
![]()
![]()
![]() Так
как
Так
как ![]() то
существует положительное число
то
существует положительное число ![]() для
которого
для
которого ![]() Отсюда
Отсюда![]() Разделив
обе части уравнения на
Разделив
обе части уравнения на ![]() получим каноническое
уравнение эллипса
получим каноническое
уравнение эллипса![]() На
самом деле уравнение (2) является
следствием уравнения эллипса. Но мы
покажем, что каждое решение уравнения
(2) является решением уравнения (1). Пусть
координаты точки
удовлетворяют
уравнению (2). Тогда расстояние от этой
точки до фокуса
равно
На
самом деле уравнение (2) является
следствием уравнения эллипса. Но мы
покажем, что каждое решение уравнения
(2) является решением уравнения (1). Пусть
координаты точки
удовлетворяют
уравнению (2). Тогда расстояние от этой
точки до фокуса
равно![]()
![]()
![]() Аналогично
вычисляется расстояние
Аналогично
вычисляется расстояние ![]() до
фокуса
до
фокуса ![]() Оно
равно
Оно
равно![]() Так
как
Так
как ![]() то
точка
лежит
на эллипсе. Тем самым доказана
эквивалентность уравнений (1) и (2) и мы
имеем полное право уравнение (2) называть
уравнением эллипса. Формулы длин
фокальных радиусов нам еще окажутся
полезными:
то
точка
лежит
на эллипсе. Тем самым доказана
эквивалентность уравнений (1) и (2) и мы
имеем полное право уравнение (2) называть
уравнением эллипса. Формулы длин
фокальных радиусов нам еще окажутся
полезными:
![]()
В
каноническое уравнение эллипса переменные
входят во второй степени. Это означает,
что оси координат являются осями
симметрии эллипса, а начало координат
- центр симметрии эллипса. Для построения
графика эллипса достаточно построить
его в первой четверти и затем отобразить
полученную линию относительно осей
координат. В первой четверти уравнение
эллипса имеет вид![]() При
возрастании
от
0 до
значение
функции уменьшается от
до
0. График выпуклый вверх. Отразив эту
линию относительно осей координат,
получим график эллипса. Точки пересечения
эллипса с его осями
При
возрастании
от
0 до
значение
функции уменьшается от
до
0. График выпуклый вверх. Отразив эту
линию относительно осей координат,
получим график эллипса. Точки пересечения
эллипса с его осями ![]()
![]()
![]()
![]() называются вершинами
эллипса,
центр симметрии эллипса
называются вершинами
эллипса,
центр симметрии эллипса ![]() - центром
эллипса,
отрезок
- большой
осью эллипса,
- центром
эллипса,
отрезок
- большой
осью эллипса, ![]() - малой
осью,
число
-большой
полуосью,
число
- малой
полуосью.
Форма эллипса зависит от расстояния
между фокусами. Если фокусы сближаются,
то эллипс становится все более похож
на окружность. Когда фокусы сольются с
центром эллипса, то эллипс обратится в
окружность с уравнением
- малой
осью,
число
-большой
полуосью,
число
- малой
полуосью.
Форма эллипса зависит от расстояния
между фокусами. Если фокусы сближаются,
то эллипс становится все более похож
на окружность. Когда фокусы сольются с
центром эллипса, то эллипс обратится в
окружность с уравнением ![]() Если
фокусы отодвигаются от центра, то эллипс
постепенно вырождается в отрезок. Основным
прямоугольником эллипса называется
прямоугольник, ограниченный прямыми,
параллельными осям эллипса и отстоящими
от них соответственно на расстоянии
и
Если
фокусы отодвигаются от центра, то эллипс
постепенно вырождается в отрезок. Основным
прямоугольником эллипса называется
прямоугольник, ограниченный прямыми,
параллельными осям эллипса и отстоящими
от них соответственно на расстоянии
и ![]() Эллипс
располагается внутри основного
прямоугольника.
Эллипс
располагается внутри основного
прямоугольника.
Рассмотрим
окружность ![]() и
подвергнем ее преобразованию
и
подвергнем ее преобразованию Получим
Получим ![]() В
результате сжатия окружности к ее оси
симметрии она преобразуется в эллипс
В
результате сжатия окружности к ее оси
симметрии она преобразуется в эллипс
Всякий
эллипс может быть получен как результат
равномерного сжатия некоторой окружности.
Степень
сжатия эллипса
характеризуется эксцентриситетом ![]() (отношение
фокусного расстояния к длине большой
оси).
Эксцентриситет эллипса всегда меньше
единицы. Для эллипса, выродившегося в
прямолинейный отрезок, эксцентриситет
равен 1. Для эллипса, превратившегося в
окружность, когда его фокусы совпали,
эксцентриситет равен нулю. Директрисой
эллипса называется
прямая, параллельная малой оси и отстоящая
от нее на расстоянии
(отношение
фокусного расстояния к длине большой
оси).
Эксцентриситет эллипса всегда меньше
единицы. Для эллипса, выродившегося в
прямолинейный отрезок, эксцентриситет
равен 1. Для эллипса, превратившегося в
окружность, когда его фокусы совпали,
эксцентриситет равен нулю. Директрисой
эллипса называется
прямая, параллельная малой оси и отстоящая
от нее на расстоянии ![]() Под
это определение попадают две прямые с
уравнениями
Под
это определение попадают две прямые с
уравнениями ![]() и
и ![]() Фокус
и директрису, лежащие в одной полуплоскости,
называем соответствующими.
Фокус
и директрису, лежащие в одной полуплоскости,
называем соответствующими.
ТЕОРЕМА. Отношение расстояния от любой точки эллипса до фокуса к расстоянию от этой точки до соответствующей директрисы равно эксцентриситету.
Доказательство.
Воспользуемся формулой длины фокального
радиуса: для левого фокуса имеем![]() Аналогично
вычисляем отношение для правого фокуса.
Аналогично
вычисляем отношение для правого фокуса.
ТЕОРЕМА. Уравнение
касательной к эллипсу ![]() в
точке
эллипса
имеет вид
в
точке
эллипса
имеет вид ![]()
Доказательство.
Продифференцировав обе части уравнения
эллипса, получим ![]()
Отсюда,
угловой коэффициент касательной в
точке ![]() равен
равен ![]() а
уравнение касательной в этой точке
можно записать так:
а
уравнение касательной в этой точке
можно записать так:
Задача. Отрезок постоянной длины скользит своими концами по двум перпендикулярным прямым. Найдите линию, описываемую некоторой точкой движущегося отрезка.
Примем
данные перпендикулярные прямые в
качестве осей координат с началом
координат в точке
пересечения
этих прямых. Точка
отрезка
скользит по оси ![]() а
точка
отрезка
скользит по оси
а
точка
отрезка
скользит по оси ![]() Пусть
точка
делит
данный отрезок
на
части
Пусть
точка
делит
данный отрезок
на
части ![]() Если
Если ![]() то
то ![]() Исключим
из этих уравнений параметр
Исключим
из этих уравнений параметр ![]()
![]() т.
е.
Таким
образом, кривая, описываемая точкой
т.
е.
Таким
образом, кривая, описываемая точкой ![]() есть
эллипс. Уравнение
есть
эллипс. Уравнение![]() называется параметрическим
уравнением эллипса.
называется параметрическим
уравнением эллипса.
a: 
b: 
OK
Задача. Луч света, выходя из одного фокуса, после отражения от эллипса попадает в другой его фокус (оптическое свойство эллипса).
Сумма
расстояний до фокусов эллипса точки
касания наименьшая среди остальных
точек касательной, поскольку все они
лежат вне эллипса. Отразим фокус
эллипса
относительно касательной к эллипсу в
точке ![]() Получим
точку
Получим
точку ![]() Точка
лежит
на отрезке
Точка
лежит
на отрезке![]() ,
так как для любой другой точки
касательной
,
так как для любой другой точки
касательной![]() По
закону: угол падения равен углу отражения,
луч движется по маршруту
По
закону: угол падения равен углу отражения,
луч движется по маршруту ![]()
Задачи и упражнения
Докажите, что если точка находится вне эллипса, то сумма расстояний от нее до фокусов больше, чем на эллипсе, если внутри, то меньше.
Докажите, что произведение расстояний от фокусов до любой касательной к эллипсу равно квадрату малой оси.
Докажите, что отрезок касательной к эллипсу в любой точке, заключенный между касательными, проведенными в вершинах, лежащих на большой оси, виден из фокусов под прямым углом.
Докажите оптическое свойство эллипса: всякая касательная к эллипсу образует равные углы с фокальными радиусами точки прикосновения.
Составьте геометрическое место точек, из которых эллипс виден под прямым углом.
Через фокус эллипса проведена хорда, касательная оси
 Определите
длину этой хорды.
Определите
длину этой хорды.Равномерным сжатием плоскости к прямой называется преобразование точек плоскости, при котором точка переходит в точку
 для
которой
для
которой  где
где  и
-
основание перпендикуляра, опущенного
из
на
прямую
Пусть
прямая
проходит
через центр данной окружности. Докажите,
что при равномерном сжатии к этой прямой
окружность преобразуется в эллипс.
и
-
основание перпендикуляра, опущенного
из
на
прямую
Пусть
прямая
проходит
через центр данной окружности. Докажите,
что при равномерном сжатии к этой прямой
окружность преобразуется в эллипс.
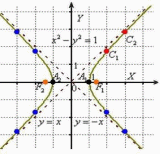
§ 12.7. Гипербола
Гиперболой называется
геометрическое место точек плоскости,
разность расстояний которых до двух
фиксированных точек этой плоскости,
постоянна. Эти две фиксированные
точки
и
называютсяфокусами.
Длина отрезка
называется фокусным
расстоянием.
Постоянную разность расстояний (из
большего расстояния вычитаем меньшее)
обозначим через
,
так что для любой точки
гиперболы
имеем ![]() .
Считаем, что
.
Считаем, что ![]() .
Для изучения гиперболы применим метод
координат. За ось абсцисс примем прямую,
проходящую
через фокусы, а серединный перпендикуляр
отрезка
за
ось ординат. Тогда координаты фокусов
и
.
Точка
принадлежит
гиперболе тогда и только тогда,
когда
.
Для изучения гиперболы применим метод
координат. За ось абсцисс примем прямую,
проходящую
через фокусы, а серединный перпендикуляр
отрезка
за
ось ординат. Тогда координаты фокусов
и
.
Точка
принадлежит
гиперболе тогда и только тогда,
когда![]() Получили
уравнение гиперболы. Преобразуем
его.
Получили
уравнение гиперболы. Преобразуем
его.![]()
![]()
![]() Так
как
Так
как ![]() ,
то существует положительное число
,
для которого
,
то существует положительное число
,
для которого ![]() Отсюда
Отсюда![]() Каноническое
уравнение гиперболы
Каноническое
уравнение гиперболы![]()
a:
b:
OK
Уравнение
(2) является следствием уравнения
гиперболы. Покажем, что каждое решение
уравнения (2) является решением уравнения
(1). Пусть координаты точки ![]() ,
удовлетворяют уравнению (2). Тогда
расстояние от этой точки до фокуса
равно
,
удовлетворяют уравнению (2). Тогда
расстояние от этой точки до фокуса
равно ![]()
Аналогично
вычисляется расстояние
до
фокуса
Оно
равно ![]() .
Так как
то
точка
лежит
на гиперболе. Тема самым доказана
эквивалентность уравнений (1) и (2) и мы
имеем полное право уравнение (2) называть
уравнением гиперболы. Формулы длин
фокальных радиусов нам еще окажутся
полезными:
.
Так как
то
точка
лежит
на гиперболе. Тема самым доказана
эквивалентность уравнений (1) и (2) и мы
имеем полное право уравнение (2) называть
уравнением гиперболы. Формулы длин
фокальных радиусов нам еще окажутся
полезными:![]()
![]()
В
каноническое уравнение гиперболы
переменные входят во второй степени.
Это означает, что оси координат являются
осями симметрии гиперболы, а начало
координат - центр симметрии гиперболы.
Для построения графика достаточно
построить его в первой четверти и затем
отобразить полученную линию относительно
осей координат. В первой четверти
уравнение гиперболы имеет вид![]()
При
возрастании
от
до
бесконечности значение функции возрастает
от
до ![]() .
График выпуклый вверх. Отразив эту линию
относительно осей координат, получим
график гиперболы. Ось симметрии гиперболы,
имеющую с ней общие точки
называем действительной
осью гиперболы.
Ось симметрии гиперболы, не имеющую с
ней общие точки называем мнимой
осью гиперболы.
Точки пересечения гиперболы с
действительной осью
.
График выпуклый вверх. Отразив эту линию
относительно осей координат, получим
график гиперболы. Ось симметрии гиперболы,
имеющую с ней общие точки
называем действительной
осью гиперболы.
Ось симметрии гиперболы, не имеющую с
ней общие точки называем мнимой
осью гиперболы.
Точки пересечения гиперболы с
действительной осью ![]() ,
, ![]() называют вершинами
гиперболы,
центр симметрии гиперболы
называют вершинами
гиперболы,
центр симметрии гиперболы ![]() - центром
гиперболы.
Гипербола распадается на две ветви:
"правую", для точек которой
абсцисса
- центром
гиперболы.
Гипербола распадается на две ветви:
"правую", для точек которой
абсцисса ![]() и
"левую", для точек которой
и
"левую", для точек которой ![]() .
.
Отношение
фокусного расстояния к расстоянию между
вершинами называется эксцентриситетом
.
Для гиперболы эксцентриситет всегда
больше 1. Директрисой
гиперболы называется
прямая, параллельная мнимой оси и
отстоящая от нее на расстоянии
Под
это определение попадают две прямые с
уравнениями
и ![]() .
Называем соответствующими фокус и
директрису, лежащие в одной полуплоскости.
.
Называем соответствующими фокус и
директрису, лежащие в одной полуплоскости.
ТЕОРЕМА. Отношение расстояния от любой точки гиперболы до фокуса к расстоянию от этой точки до соответствующей директрисы равно эксцентриситету.
Доказательство.
Воспользуемся формулой длины фокального
радиуса: для левого фокуса
при ![]() имеем
Аналогично
вычисляем отношение в остальных случаях.
имеем
Аналогично
вычисляем отношение в остальных случаях.
Продолжим
изучение гиперболы в первой четверти.
Положительная в первой четверти разность
между ординатами прямой и гиперболы![]() cтремится
к нулю при бесконечном возрастании
.
Прямая
cтремится
к нулю при бесконечном возрастании
.
Прямая![]() является асимптотой гиперболы.
При бесконечном возрастании
гипербола
приближается к прямой, но не пересекает.
В силу симметрии такая же картина
наблюдается в третьей четверти, а во
второй и четвертой четвертях асимптотой
является прямая
является асимптотой гиперболы.
При бесконечном возрастании
гипербола
приближается к прямой, но не пересекает.
В силу симметрии такая же картина
наблюдается в третьей четверти, а во
второй и четвертой четвертях асимптотой
является прямая![]() Точка
Точка ![]() лежит
на асимптоте, т. е. геометрический смысл
параметра
-
ордината асимптоты, восставленная из
вершины гиперболы. Так как
лежит
на асимптоте, т. е. геометрический смысл
параметра
-
ордината асимптоты, восставленная из
вершины гиперболы. Так как![]() то
для нахождения фокуса гиперболы можно
отложить на оси
отрезок
то
для нахождения фокуса гиперболы можно
отложить на оси
отрезок ![]() .
.
Основным прямоугольником гиперболы называется прямоугольник, ограниченный прямыми, параллельными осям гиперболы и отстоящими от них соответственно на расстоянии и . Диагонали основного прямоугольника гиперболы и есть асимптоты.
Упражнения
Докажите, что уравнение касательной к гиперболе
 в
точке
гиперболы
имеет вид
в
точке
гиперболы
имеет вид 
Точка называется внутренней точкой гиперболы, если любая секущая, проходящая через эту точку и не параллельная асимптотам, пересекает гиперболу в двух различных точках. Внешней точкой гиперболы называется точка, не лежащая на гиперболе и не являющаяся внутренней. Докажите, что точка внутренняя точка гиперболы в том и только том случае, если

Найдите необходимое и достаточное условие касания прямой
 с
гиперболой
,
если данная прямая не параллельна
асимптотам гиперболы.
с
гиперболой
,
если данная прямая не параллельна
асимптотам гиперболы.Найдите необходимое и достаточное условие касания прямой
 с
гиперболой
,
если данная прямая не параллельна
асимптотам гиперболы.
с
гиперболой
,
если данная прямая не параллельна
асимптотам гиперболы.Докажите, что касательные в вершинах гиперболы, параллельны ее мнимой оси.
Если угловой коэффициент прямой удовлетворяет неравенствам
 ,
то прямая не может касаться
гиперболы
Докажите
это.
,
то прямая не может касаться
гиперболы
Докажите
это.Найдите геометрическое место точек плоскости, из которых гипербола видна под прямым углом.
Докажите, что произведение расстояний от фокусов до любой касательной к гиперболе есть величина постоянная.
Докажите, что отрезок асимптоты, заключенный между центром гиперболы и директрисой, равен действительной полуоси.
Докажите, что директрисы гиперболы проходят через основания перпендикуляров, опущенных из соответствующих фокусов на асимптоты. Выразите расстояние от фокусов до асимптот через полуоси гиперболы.
Докажите, что отрезок касательной к гиперболе, заключенный между асимптотами, делится в точке соприкосновения пополам.
Докажите оптическое свойство гиперболы: всякая касательная к гиперболе составляет равные углы с фокальными радиусами точки касания.
§ 12.8. Парабола
Параболой называется
геометрическое место точек плоскости,
равноудаленных от данной точки и данной
прямой этой плоскости. Данная
точка ![]() называется фокусом,
а данная прямая называется директрисой.
Расстояние
между
фокусом и директрисой называется фокальным
параметром или параметром
параболы.
называется фокусом,
а данная прямая называется директрисой.
Расстояние
между
фокусом и директрисой называется фокальным
параметром или параметром
параболы.
Для
изучения параболы применим метод
координат. За ось абсцисс примем прямую,
проходящую через фокус перпендикулярно
директрисе; за ось ординат - прямую,
параллельную директрисе и проходящую
на равном расстоянии от фокуса и
директрисы. Координаты фокуса ![]() .
Точка
принадлежит
параболе тогда и только тогда, когда
.
Точка
принадлежит
параболе тогда и только тогда, когда![]() Это
- уравнение параболы. Преобразуем
его.
Это
- уравнение параболы. Преобразуем
его.![]() Получили каноническое
уравнение параболы
Получили каноническое
уравнение параболы![]() Каждому
положительному значению х отвечают два
значения
Каждому
положительному значению х отвечают два
значения![]() а
может
принимать только положительные значения
и нуль. График симметричен относительно
оси
.
Точка пересечения параболы с ее осью
называется вершиной параболы.
а
может
принимать только положительные значения
и нуль. График симметричен относительно
оси
.
Точка пересечения параболы с ее осью
называется вершиной параболы.
p:
OK
Упражнения
Докажите, что уравнение касательной к параболе
 в
точке
параболы
имеет вид
в
точке
параболы
имеет вид
Найдите геометрическое место середин хорд параболы , имеющих угловой коэффициент
 .
.Прямая , не параллельная оси касается параболы тогда и только тогда, когда
 .
Докажите это.
.
Докажите это.Прямая , не параллельная оси , касается параболы тогда и только тогда, когда
 .
Докажите это.
.
Докажите это.Точка называется внутренней точкой параболы, если любая прямая, проходящая через эту точку и не параллельная оси параболы, пересекает параболу в двух различных точках. Внешней точкой параболы называется точка, не лежащая на параболе и не являющаяся внутренней. Докажите, что точка внутренняя точка параболы в том и только том случае, если

Найдите геометрическое место оснований перпендикуляров, опущенных из фокуса параболы на ее касательные.
Найдите геометрическое место точек плоскости, из которых парабола видна под прямым углом.
Если из любой точки директрисы проведены к параболе две касательные, то прямая, соединяющая точки касания, проходит через фокус параболы. Докажите это.
Докажите оптическое свойство параболы: всякая касательная к параболе составляет равные углы с фокальным радиусом точки и лучом, проходящим через точку касания и сонаправленным с осью.
Докажите, что произведение длин перпендикуляров, опущенных из концов любой фокальной хорды на ось параболы имеет постоянную величину.
§ 12.9. Полярное уравнение линии второго порядка
Найдем
уравнение эллипса, гиперболы и параболы
в полярных координатах. Начало полярной
системы координат поместим в фокус
(левый в случае эллипса, правый в случае
гиперболы). Полярная ось направлена по
фокальной оси в сторону, противоположную
от соответствующей директрисы. Для
произвольной точки
кривой
обозначим через
расстояние
от точки
до
фокуса
,
а через
-
расстояние от
до
директрисы. Наша кривая есть геометрическое
место точек, для которых ![]() где
где ![]() -
эксцентриситет эллипса или гиперболы
и
-
эксцентриситет эллипса или гиперболы
и ![]() в
случае параболы. Пусть
-
точка пересечения прямой, проведенной
через
,
перпендикулярно полярной оси и
в
случае параболы. Пусть
-
точка пересечения прямой, проведенной
через
,
перпендикулярно полярной оси и ![]() Обозначая
через
Обозначая
через ![]() точку
пересечения директрисы с фокальной
осью, а через
-
проекцию точки
на
эту ось, получим, что
точку
пересечения директрисы с фокальной
осью, а через
-
проекцию точки
на
эту ось, получим, что ![]() или
или![]() где
-
угол наклона вектора
где
-
угол наклона вектора ![]() к
полярной оси.
к
полярной оси.![]()
![]()
![]() Это
и есть уравнение эллипса, правой ветви
гиперболы и параболы в полярных
координатах. Этими уравнениями постоянно
пользуются в астрономии и в механике.
Это
и есть уравнение эллипса, правой ветви
гиперболы и параболы в полярных
координатах. Этими уравнениями постоянно
пользуются в астрономии и в механике.
§ 12.10. Общая теория линий второго порядка
Линией
второго порядка называется линия,
которая в некоторой декартовой системе
координат определяется уравнением
второй степени. Запишем уравнение
второго порядка в самом общем виде![]() При
условии, что
При
условии, что ![]() вычислим
вычислим ![]()
ПРИМЕР.
Для эллипса
имеем ![]()
![]() .
Тогда
.
Тогда

Можно
доказать, что эти числа являются
инвариантами относительно преобразования
параллельного переноса, т. е. при
преобразовании поворота осей
координат![]() величины,
составленные из соответствующих
коэффициентов преобразованного
уравнения, сохранятся. Можно доказать
также, что при параллельном переносе
осей координат
величины,
составленные из соответствующих
коэффициентов преобразованного
уравнения, сохранятся. Можно доказать
также, что при параллельном переносе
осей координат![]() не
изменяются величины
не
изменяются величины ![]() и
и ![]() .
Таким образом, можно определить название
линии второго порядка.
.
Таким образом, можно определить название
линии второго порядка.
С помощью параллельного переноса системы координат можно освободиться от слагаемых первой степени, а с помощью поворота осей можно освободиться от слагаемого, содержащего произведение переменных. После подбора подходящей системы координат уравнение второй степени примет наиболее простой вид. Коэффициенты приведенных уравнений определяются при помощи инвариантов.
Упражнения
Центром линии называется точка плоскости, по отношению к которой точки линии симметричны парами. Линии второго порядка, обладающие центром, называются центральными. Докажите, что точка
 является
центром линии (1) тогда и только тогда,
когда
является
центром линии (1) тогда и только тогда,
когда
Определитель второго порядка
 ,
составленный из коэффициентов при
старших слагаемых уравнения (1),
называется дискриминантом
уравнения (1).
Докажите, что линия второго порядка
центральная тогда и только тогда,
когда
,
составленный из коэффициентов при
старших слагаемых уравнения (1),
называется дискриминантом
уравнения (1).
Докажите, что линия второго порядка
центральная тогда и только тогда,
когда  .
Докажите, что координаты центра находятся
по формулам
.
Докажите, что координаты центра находятся
по формуламОпределитель
 называется
дискриминантом левой части уравнения
(1); здесь
называется
дискриминантом левой части уравнения
(1); здесь  и
и  для
для  ю
При переносе начала координат в центр
линии (1) с помощью преобразования
ю
При переносе начала координат в центр
линии (1) с помощью преобразования  уравнение
(1) приобрело вид
уравнение
(1) приобрело вид Докажите,
что
Докажите,
что 
Установите, что следующие линии являются центральными, и найдите координаты центра каждой линии:
а)

б)

в)

г)

Уравнение (2) подвергнем преобразованию поворота осей на угол
 при
условии, что
при
условии, что  Докажите,
что в новых координатах уравнение линии
примет вид
Докажите,
что в новых координатах уравнение линии
примет вид  где
где  и
и 
Уравнение второй степени называется эллиптическим, если
 ,
гиперболическим, если
,
гиперболическим, если  и
параболическим, если
и
параболическим, если  .
Докажите, что уравнение центральной
линии может быть только эллиптическим
или гиперболическим.
.
Докажите, что уравнение центральной
линии может быть только эллиптическим
или гиперболическим.Докажите, что каждое эллиптическое уравнение является уравнением эллипса, либо вырожденного эллипса, либо мнимого эллипса.
Докажите, что каждое гиперболическое уравнение определяет уравнение гиперболы либо вырожденной гиперболы.
Докажите, что если , то линия либо не имеет центра, либо имеет бесконечно много центров.
Уравнение (1) подвергнем преобразованию поворота осей на угол
 при
условии, что
и
при
условии, что
и  .
Докажите, что в новых координатах
уравнение линии примет вид
.
Докажите, что в новых координатах
уравнение линии примет вид где
где  ,
либо вид
,
либо вид где
где 
Гипербола и её каноническое уравнение
Общая структура изложения материала будет напоминать предыдущий параграф. Начнём с общего понятия гиперболы и задачи на её построение.
Каноническое
уравнение гиперболы имеет вид 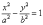 ,
где
,
где 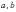 –
положительные действительные числа.
Обратите внимание, что в отличие
от эллипса,
здесь не накладывается условие
–
положительные действительные числа.
Обратите внимание, что в отличие
от эллипса,
здесь не накладывается условие 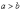 ,
то есть, значение «а» может быть и меньше
значения «бэ».
,
то есть, значение «а» может быть и меньше
значения «бэ».
Надо
сказать, довольно неожиданно… уравнение
«школьной» гиперболы 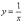 и
близко не напоминает каноническую
запись. Но эта загадка нас ещё подождёт,
а пока почешем затылок и вспомним, какими
характерными особенностями обладает
рассматриваемая кривая? Раскинем на
экране своего воображения график
функции
….
и
близко не напоминает каноническую
запись. Но эта загадка нас ещё подождёт,
а пока почешем затылок и вспомним, какими
характерными особенностями обладает
рассматриваемая кривая? Раскинем на
экране своего воображения график
функции
….
У гиперболы две симметричные ветви.
У гиперболы две асимптоты.
Неплохой прогресс! Данными свойствами обладает любая гипербола, и сейчас мы с неподдельным восхищением заглянем в декольте этой линии:
Пример 4
Построить
гиперболу, заданную уравнением 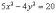
Решение:
на первом шаге приведём данное уравнение
к каноническому виду
.
Пожалуйста, запомните типовой порядок
действий. Справа необходимо получить
«единицу», поэтому обе части исходного
уравнения делим на 20:
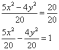
Здесь
можно сократить обе дроби, но оптимальнее
сделать каждую из них трёхэтажной:
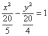
И
только после этого провести сокращение:
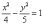
Выделяем
квадраты в знаменателях:
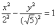
Готово.
Почему
преобразования лучше проводить именно
так? Ведь дроби левой части 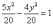 можно
сразу сократить и получить
.
Дело в том, что в рассматриваемом примере
немного повезло: число 20 делится и на 4
и на 5. В общем случае такой номер не
проходит. Рассмотрим, например,
уравнение
можно
сразу сократить и получить
.
Дело в том, что в рассматриваемом примере
немного повезло: число 20 делится и на 4
и на 5. В общем случае такой номер не
проходит. Рассмотрим, например,
уравнение 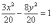 .
Здесь с делимостью всё печальнее и
без трёхэтажных
дробей уже
не обойтись:
.
Здесь с делимостью всё печальнее и
без трёхэтажных
дробей уже
не обойтись:
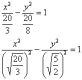
Итак, воспользуемся плодом наших трудов – каноническим уравнением :
Как построить гиперболу?
Существует два подхода к построению гиперболы – геометрический и алгебраический. С практической точки зрения вычерчивание с помощью циркуля... я бы даже сказал утопично, поэтому гораздо выгоднее вновь привлечь на помощь нехитрые расчёты.
Целесообразно придерживаться следующего алгоритма, сначала готовый чертёж, потом комментарии:
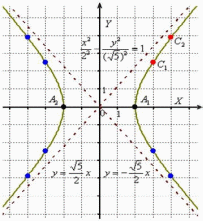
1)
Прежде всего, находим асимптоты.
Если гипербола задана каноническим
уравнением
,
то её асимптотами являются прямые 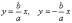 .
В нашем случае:
.
В нашем случае: 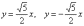 . Данный
пункт обязателен! Это
принципиальная особенность чертежа, и
будет грубой ошибкой, если ветви гиперболы
«вылезут» за свои асимптоты.
. Данный
пункт обязателен! Это
принципиальная особенность чертежа, и
будет грубой ошибкой, если ветви гиперболы
«вылезут» за свои асимптоты.
2)
Теперь находим две
вершины гиперболы,
которые расположены на оси абсцисс в
точках  .
Выводится элементарно: если
.
Выводится элементарно: если 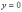 ,
то каноническое уравнение
превращается
в
,
то каноническое уравнение
превращается
в 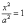 ,
откуда и следует, что
,
откуда и следует, что 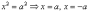 .
Рассматриваемая гипербола имеет
вершины
.
Рассматриваемая гипербола имеет
вершины 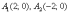
3)
Ищем дополнительные точки. Обычно
хватает 2-3-х. В каноническом положении
гипербола симметрична относительно
начала координат и обеих координатных
осей, поэтому вычисления достаточно
провести для 1-ой координатной четверти.
Методика точно такая же, как и при
построении эллипса.
Из канонического уравнения
на
черновике выражаем:
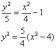 Уравнение
распадается на две функции:
Уравнение
распадается на две функции:
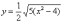 –
определяет верхние дуги гиперболы (то,
что нам надо);
–
определяет верхние дуги гиперболы (то,
что нам надо);
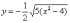 –
определяет нижние дуги гиперболы.
–
определяет нижние дуги гиперболы.
Напрашивается
нахождение точек с абсциссами 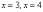 :
:
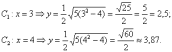
4)
Изобразим на чертеже асимптоты
,
вершины
,
дополнительные 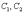 и
симметричные им точки в других координатных
четвертях. Аккуратно соединим
соответствующие точки у каждой ветви
гиперболы:
и
симметричные им точки в других координатных
четвертях. Аккуратно соединим
соответствующие точки у каждой ветви
гиперболы:
Техническая
трудность может возникнуть с
иррациональным угловым
коэффициентом 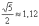 ,
но это вполне преодолимая проблема.
,
но это вполне преодолимая проблема.
Отрезок 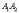 называют действительной
осью гиперболы,
его
длину
называют действительной
осью гиперболы,
его
длину 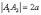 –
расстоянием между
вершинами;
число
–
расстоянием между
вершинами;
число  называют действительной
полуосью гиперболы;
число
называют действительной
полуосью гиперболы;
число  – мнимой
полуосью.
– мнимой
полуосью.
В
нашем примере: 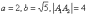 ,
и, очевидно, если данную гиперболу
повернуть вокруг центра симметрии и/или
переместить, то эти значения не
изменятся.
,
и, очевидно, если данную гиперболу
повернуть вокруг центра симметрии и/или
переместить, то эти значения не
изменятся.
Определение гиперболы. Фокусы и эксцентриситет
У
гиперболы, точно так же, как и у эллипса,
есть две особенные точки 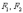 ,
которые называются фокусами. Не
говорил, но на всякий случай, вдруг кто
неверно понимает: центр симметрии и
точки фокуса, разумеется, не принадлежат
кривым.
,
которые называются фокусами. Не
говорил, но на всякий случай, вдруг кто
неверно понимает: центр симметрии и
точки фокуса, разумеется, не принадлежат
кривым.
Общая концепция определения тоже похожа:
Гиперболой называют
множество всех точек плоскости, абсолютное
значение разности
расстояний до каждой из которых от двух
данных точек
–
есть величина постоянная, численно
равная расстоянию между вершинами этой
гиперболы: 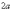 .
При этом расстояние между фокусами
превосходит длину действительной
оси:
.
При этом расстояние между фокусами
превосходит длину действительной
оси: 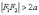 .
.
Если
гипербола задана каноническим
уравнением
,
то расстояние
от центра симметрии до каждого из
фокусов рассчитывается
по формуле: 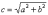 .
И,
соответственно, фокусы имеют координаты
.
И,
соответственно, фокусы имеют координаты 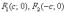 .
.
Для
исследуемой гиперболы
:
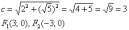
Разбираемся
в определении. Обозначим через 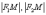 расстояния
от фокусов до произвольной
точки
расстояния
от фокусов до произвольной
точки 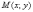 гиперболы:
гиперболы:
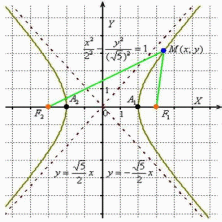
Сначала
мысленно передвигайте синюю точку по
правой ветви гиперболы – где бы мы ни
находились, модуль (абсолютное
значение) разности между длинами
отрезков  будет
одним и тем же:
будет
одним и тем же:
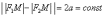
Если точку «перекинуть» на левую ветвь, и перемещать её там, то данное значение останется неизменным.
Знак
модуля нужен по той причине, что разность
длин  может
быть как положительной, так и отрицательной.
Кстати, для любой точки правой
ветви
может
быть как положительной, так и отрицательной.
Кстати, для любой точки правой
ветви 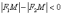 (поскольку
отрезок
(поскольку
отрезок 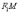 короче
отрезка
короче
отрезка 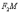 ).
Для любой точки
левой
ветви ситуация ровно противоположная
и
).
Для любой точки
левой
ветви ситуация ровно противоположная
и 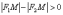 .
.
Более
того, ввиду очевидного свойства
модуля  безразлично,
что из чего вычитать.
безразлично,
что из чего вычитать.
Удостоверимся,
что в нашем примере модуль данной
разности действительно равен расстоянию
между вершинами. Мысленно поместите
точку
в
правую вершину гиперболы 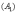 .
Тогда:
.
Тогда: 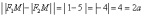 ,
что и требовалось проверить.
,
что и требовалось проверить.
Эксцентриситетом гиперболы
называют отношение 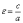 .
.
Так
как расстояние от центра до фокуса
больше расстояния от центра до вершины: 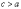 ,
то эксцентриситет гиперболы всегда
больше «единицы»:
,
то эксцентриситет гиперболы всегда
больше «единицы»: 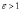 .
.
Для
данного примера: 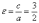 .
.
По
аналогии с эллипсом,
зафиксировав значение 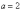 ,
желающие могут провести самостоятельный
анализ и проверку следующих фактов:
,
желающие могут провести самостоятельный
анализ и проверку следующих фактов:
При
увеличении эксцентриситета ветви
гиперболы «распрямляются» к оси 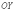 .
В
предельном случае
.
В
предельном случае  они
стремятся занять положение двух прямых,
проходящих через точки
они
стремятся занять положение двух прямых,
проходящих через точки 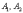 параллельно
оси ординат.
параллельно
оси ординат.
Если
же значение эксцентриситета приближается
к единице, то ветви гиперболы «сплющиваются»
к оси 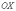 .
.
Равносторонняя гипербола
На
практике часто встречается гипербола
с равными полуосями. Если  ,
то каноническое уравнение
заметно
упрощается:
,
то каноническое уравнение
заметно
упрощается:
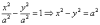
А
вместе с ним упрощаются и уравнения
асимптот:

Прямые 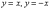 пересекаются
под прямым углом и «справедливо» делят
координатную плоскость на 4 одинаковые
части, в двух из которых находятся ветви
кривой. Образно говоря, равносторонняя
гипербола «идеально сложена», то есть
и не растянута и не сплющена.
пересекаются
под прямым углом и «справедливо» делят
координатную плоскость на 4 одинаковые
части, в двух из которых находятся ветви
кривой. Образно говоря, равносторонняя
гипербола «идеально сложена», то есть
и не растянута и не сплющена.
Так
как
,
то  ,
следовательно, эксцентриситет любой
равносторонней гиперболы равен:
,
следовательно, эксцентриситет любой
равносторонней гиперболы равен: 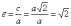 .
.
Предлагаю закрепить теорию и практические навыки миниатюрной задачей:
Пример 5
Построить
гиперболу  и
найти её фокусы.
и
найти её фокусы.
Это пример для самостоятельного решения. Кто пропустит, тот пропустит многое ;-) Решение и чертёж в конце урока.
Начнём тревожить беззаботное существование нашей кривой:
Поворот вокруг центра и параллельный перенос гиперболы
Вернёмся
к демонстрационной гиперболе
.
Что произойдёт, если в полученном
уравнении поменять значения
полуосей: 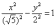 ?
Для эллипса данный трюк означал поворот
на 90 градусов. Но здесь всё иначе!
Уравнение
определяет совершенно
другую гиперболу.
Ну, хотя бы обратите внимание на иные
вершины:
?
Для эллипса данный трюк означал поворот
на 90 градусов. Но здесь всё иначе!
Уравнение
определяет совершенно
другую гиперболу.
Ну, хотя бы обратите внимание на иные
вершины: 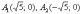 .
.
Теперь
рассмотрим уравнение 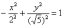 ,
которое очевидно тоже задаёт гиперболу.
Однако к исходному уравнению оно также
не имеет никакого отношения! Это
предыдущая гипербола, повёрнутая на 90
градусов, с вершинами
,
которое очевидно тоже задаёт гиперболу.
Однако к исходному уравнению оно также
не имеет никакого отношения! Это
предыдущая гипербола, повёрнутая на 90
градусов, с вершинами 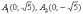 на
оси ординат.
на
оси ординат.
И,
наконец, оставшийся случай 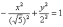 задаёт
нашу гиперболу
,
повернутую на 90 градусов. Как быть, если
в практической задаче встретилась такая
неканоническая запись?
задаёт
нашу гиперболу
,
повернутую на 90 градусов. Как быть, если
в практической задаче встретилась такая
неканоническая запись?
Если
требуется только построить кривую, то,
наверное, лучше построить её в нестандартном
виде. Это довольно просто. Уравнения
асимптот гиперболы
обладают обратными угловыми
коэффициентами:
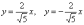
Поскольку
оси «поменялись ролями», то вершины
будут расположены на оси ординат в
точках 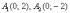 .
Выразим верхнюю ветвь гиперболы:
.
Выразим верхнюю ветвь гиперболы:
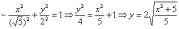
И
найдём несколько дополнительных точек:
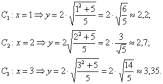
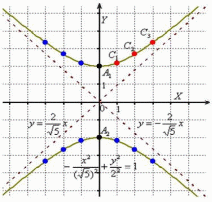
Выполним
чертёж:
 Помимо
геометрии, похожие графики требуется
строить в некоторых задачах математического
анализа.
Помимо
геометрии, похожие графики требуется
строить в некоторых задачах математического
анализа.
Однако по возможности всё-таки лучше осуществить поворот на 90 градусов и переписать уравнение в канонической форме. Для этого следует поменять местами значения полуосей и переставить «минус» к переменной «игрек»: . И далее работать уже с каноническим уравнением.
! Примечание: строгий теоретический подход предполагает поворот координатных осей, а не самой линии. При необходимости оформляйте решение по аналогии с соответствующим примечанием предыдущего урока.
Параллельный
перенос. Уравнение 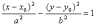 задаёт
гиперболу с действительной полуосью
«а», мнимой полуосью «бэ» и центром в
точке
задаёт
гиперболу с действительной полуосью
«а», мнимой полуосью «бэ» и центром в
точке 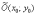 .
.
Так,
например, гипербола 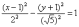 имеет
центр симметрии в точке
имеет
центр симметрии в точке 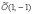 .
Асимптоты, само собой, переместились
вместе с гиперболой, их уравнения
отыскиваются по формулам:
.
Асимптоты, само собой, переместились
вместе с гиперболой, их уравнения
отыскиваются по формулам:
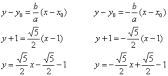
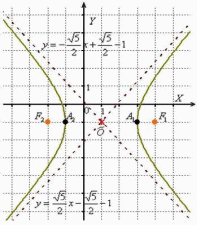
Полуоси 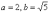 и
расстояние от фокусов до центра
симметрии
и
расстояние от фокусов до центра
симметрии  остались
прежними, а вот координаты фокусов
изменились с учётом параллельного
переноса:
остались
прежними, а вот координаты фокусов
изменились с учётом параллельного
переноса:
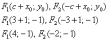
Параллельный
перенос гиперболы доставил заметно
больше хлопот, чем параллельный
перенос эллипса,
смотрим на картинку:
После таких трудов, уравнение трогать бессмысленно, но если таки просят, то придётся….
В
нестрогом варианте: «Приведём уравнение
гиперболы
к каноническому виду путём параллельного
переноса в начало координат: 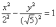 ».
».
Или в строгом – с параллельным переносом системы координат началом в точку (см. шаблон у эллипса).
На практике часто встречается комбинация поворота на произвольный угол и параллельного переноса гиперболы. Данная ситуация рассматривается на урокеПриведение уравнения линии 2-го порядка к каноническому виду.
Парабола и её каноническое уравнение
Свершилось!
Она самая. Готовая раскрыть немало тайн.
Каноническое уравнение параболы имеет
вид 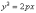 ,
где
,
где 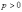 –
действительное число. Нетрудно заметить,
что в своём стандартном положении
парабола «лежит на боку» и её вершина
находится в начале координат. При этом
функция
–
действительное число. Нетрудно заметить,
что в своём стандартном положении
парабола «лежит на боку» и её вершина
находится в начале координат. При этом
функция 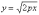 задаёт
верхнюю ветвь данной линии, а функция
задаёт
верхнюю ветвь данной линии, а функция 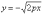 –
нижнюю ветвь. Очевидно, что парабола
симметрична относительно оси
.
Собственно, чего париться:
–
нижнюю ветвь. Очевидно, что парабола
симметрична относительно оси
.
Собственно, чего париться:
Пример 6
Построить
параболу 
Решение:
вершина известна, найдём дополнительные
точки. Уравнение 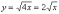 определяет
верхнюю дугу параболы, уравнение
определяет
верхнюю дугу параболы, уравнение 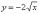 –
нижнюю дугу.
–
нижнюю дугу.
В
целях сократить запись вычисления
проведём «под одной гребёнкой» 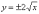 :
:
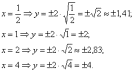
Для компактной записи результаты можно было свести в таблицу.
Перед тем, как выполнить элементарный поточечный чертёж, сформулируем строгое
Определение параболы:
Параболой
называется множество всех точек
плоскости, равноудалённых от данной
точки 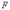 и данной прямой
и данной прямой 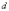 ,
не проходящей через точку
.
,
не проходящей через точку
.
Точка
называется фокусом параболы,
прямая
– директрисой (пишется
с одной «эс») параболы.
Константа «пэ» канонического
уравнения
называетсяфокальным
параметром,
который равен расстоянию от фокуса до
директрисы. В данном случае 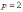 .
При этом фокус имеет координаты
.
При этом фокус имеет координаты 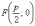 ,
а директриса задаётся уравнением
,
а директриса задаётся уравнением 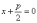 .
В
нашем примере
.
В
нашем примере  :
:
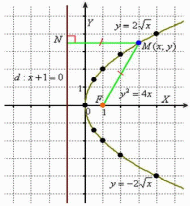 Определение
параболы понимается ещё проще, чем
определения эллипса и гиперболы. Для
любой точки
параболы
длина отрезка
Определение
параболы понимается ещё проще, чем
определения эллипса и гиперболы. Для
любой точки
параболы
длина отрезка 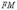 (расстояние
от фокуса до точки) равна длине
перпендикуляра
(расстояние
от фокуса до точки) равна длине
перпендикуляра  (расстоянию
от точки до директрисы):
(расстоянию
от точки до директрисы):
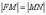
Поздравляю! Многие из вас сегодня сделали самое настоящие открытие. Оказывается, гипербола и парабола вовсе не являются графиками «рядовых» функций, а имеют ярко выраженное геометрическое происхождение.
Очевидно, что при увеличении фокального параметра ветви графика будут «раздаваться» вверх и вниз, бесконечно близко приближаясь к оси . При уменьшении же значения «пэ» они начнут сжиматься и вытягиваться вдоль оси
Эксцентриситет
любой параболы равен единице: 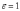
Поворот и параллельный перенос параболы
Парабола – одна из самых распространённых линий в математике, и строить её придётся действительно часто. Поэтому, пожалуйста, особенно внимательно отнестись к заключительному параграфу урока, где я разберу типовые варианты расположения данной кривой.
! Примечание: как и в случаях с предыдущими кривыми, корректнее говорить о повороте и параллельном переносе координатных осей, но автор ограничится упрощённым вариантом изложения, чтобы у читателя сложились элементарные представления о данных преобразованиях.
1)
Поворот вокруг вершины.
Если в уравнении присутствует знак
«минус»:  ,
то это означает разворот
параболы на 180 градусов относительно
своего канонического положения.
А если в уравнении
переменные
«поменялись местами»:
,
то это означает разворот
параболы на 180 градусов относительно
своего канонического положения.
А если в уравнении
переменные
«поменялись местами»: 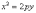 ,
то это означает поворот
канонической параболы на 90 градусов
против часовой стрелки.
,
то это означает поворот
канонической параболы на 90 градусов
против часовой стрелки.
На
следующем чертеже изображены графики
кривых  :
:
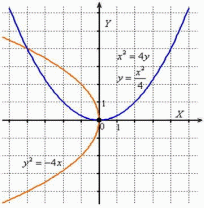 Оба
уравнения задают неканоническое
расположение нашей подопытной параболы
,
причём во втором случае легко получить
функциональную запись, к которой мы
привыкли в курсе математического
анализа:
Оба
уравнения задают неканоническое
расположение нашей подопытной параболы
,
причём во втором случае легко получить
функциональную запись, к которой мы
привыкли в курсе математического
анализа:  .
.
Таким
образом, все параболы, с которыми мы
обычно работаем – не каноничны! Я очень
хотел «уложить на бок» классическую
параболу 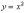 и
разобрать каноническое уравнение
и
разобрать каноническое уравнение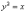 ,
но, к сожалению, у неё достаточно малый
фокальный параметр
,
но, к сожалению, у неё достаточно малый
фокальный параметр  ,
и чертеж с точкой фокуса
,
и чертеж с точкой фокуса 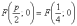 ,
директрисой
,
директрисой 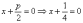 был
бы крайне невразумителен.
был
бы крайне невразумителен.
2)
Параллельный перенос.
Без всякой оригинальности. Уравнение 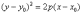 задаёт
ту же параболу
с
вершиной в точке
.
По моим наблюдениям, во многих задачах
матана очень популярен частный случай
задаёт
ту же параболу
с
вершиной в точке
.
По моим наблюдениям, во многих задачах
матана очень популярен частный случай
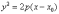 –
когда каноническая парабола сдвигается
влево или вправо по оси абсцисс. Ну, и
как дополнительная опция, разворачивается,
если при переменной «икс» есть знак
«минус».
–
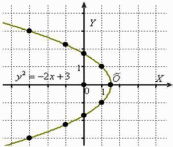
когда каноническая парабола сдвигается
влево или вправо по оси абсцисс. Ну, и
как дополнительная опция, разворачивается,
если при переменной «икс» есть знак
«минус».
Соответствующее творческое задание для самостоятельного решения:
Пример 7
Построить
параболу  .
Привести уравнение линии к каноническому
виду, найти фокус и уравнение директрисы.
.
Привести уравнение линии к каноническому
виду, найти фокус и уравнение директрисы.
Как лучше действовать?
По
условию требуется построить параболу
.
Именно такую – в неканоническом виде!
Поэтому в первой части задачи следует
представить уравнение в виде
,
что позволит сразу определить вершину.
Затем по образцу Примера 6 нужно провести
поточечное построение линии, работая
с уравнениями 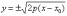 .
.
Вторая часть задания предполагает приведение уравнения к каноническому виду. Проанализируйте равенство – есть ли поворот, есть ли параллельный перенос? После того, как выясните каноническую запись , необходимо найти фокус параболы и уравнение её директрисы. Обратите внимание, что в контексте условия это, вероятнее всего, нужно сделать в каноническом положении!
Ну, а наша обзорная экскурсия подошла к концу, и я надеюсь, что у вас не возникло и не возникнет трудностей с тремя атлантами темы – эллипсом, гиперболой и параболой. Предлагаю узнать новый теоретический материал и закрепить практические навыки на уроке Задачи с линиями 2-го порядка.
Желаю успехов!
Решения и чертежи:
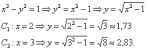 Определим
координаты фокусов:
Определим
координаты фокусов: 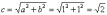
 Выполним
чертёж:
Выполним
чертёж:
 Перед
вами «школьная» гипербола в
каноническом положении. График
функции
получается
путём поворота (вокруг начала координат)
построенного графика
на
45 градусов против часовой стрелки (а
если строже – путём поворота системы
координат на противоположно ориентированный
угол в «минус» 45 градусов).
Перед
вами «школьная» гипербола в
каноническом положении. График
функции
получается
путём поворота (вокруг начала координат)
построенного графика
на
45 градусов против часовой стрелки (а
если строже – путём поворота системы
координат на противоположно ориентированный
угол в «минус» 45 градусов).
И
в общем случае – график обратной
пропорциональности  представляет
собой равностороннюю гиперболу, уравнение
которой можно привести к каноническому
виду
представляет
собой равностороннюю гиперболу, уравнение
которой можно привести к каноническому
виду 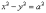 .
.
Пример
7: Решение:
преобразуем уравнение:
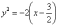 Вершина
параболы находится в точке
Вершина
параболы находится в точке 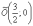 ,
ветви направлены влево. С помощью
уравнений
,
ветви направлены влево. С помощью
уравнений 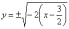 найдём
дополнительные точки:
найдём
дополнительные точки:
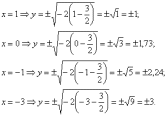 Выполним
чертёж:
Выполним
чертёж:
 Парабола
получена
путём поворота параболы
Парабола
получена
путём поворота параболы 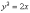 на
180 градусов и её параллельного переноса
в точку
.
Из канонического уравнения
на
180 градусов и её параллельного переноса
в точку
.
Из канонического уравнения 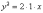 находим
фокальный параметр
находим
фокальный параметр 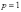 ,
фокус
,
фокус 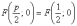 и
уравнение директрисы
и
уравнение директрисы 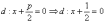 .
Примечание:
в случае необходимости нетрудно найти
координаты фокуса и уравнение директрисы
неканонически расположенной параболы
.
Учитывая поворот и параллельный
перенос:
.
Примечание:
в случае необходимости нетрудно найти
координаты фокуса и уравнение директрисы
неканонически расположенной параболы
.
Учитывая поворот и параллельный
перенос: 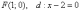 .
.
Гиперболоид
[править | править вики-текст]
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Гиперболоид (значения).

Однополостный гиперболоид

Двуполостный гиперболоид
Гиперболоид (от др.-греч. ὑπερβολή — гипербола, и εἶδος — вид, внешность). В математике гиперболоид — это видповерхности второго порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением
 (однополостный
гиперболоид),
(однополостный
гиперболоид),
где a и b — действительные полуоси, а c — мнимая полуось;
или
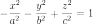 (двуполостный
гиперболоид),
(двуполостный
гиперболоид),
где a и b — мнимые полуоси, а c — действительная полуось.
Если a = b,
то такая поверхность называется гиперболоидом
вращения.
Однополостный гиперболоид вращения
может быть получен
вращением гиперболы вокруг
её мнимой оси, двухполостный — вокруг
действительной. Двуполостный гиперболоид
вращения также является геометрическим
местом точек P,
модуль разности расстояний от которых
до двух заданных точек A и B постоянен: 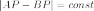 .
В этом случае A и B называютсяфокусами гиперболоида.
.
В этом случае A и B называютсяфокусами гиперболоида.
Однополостный гиперболоид является дважды линейчатой поверхностью; если он является гиперболоидом вращения, то он может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней.
Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.
Канонические уравнения параболоида в декартовых координатах:

если
 и
и  одного
знака, то параболоид называется
эллиптическим.
одного
знака, то параболоид называется
эллиптическим.если и разного знака, то параболоид называется гиперболическим.
если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром.
Эллипти́ческий параболо́ид — поверхность, задаваемая функцией вида
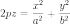 .
.Эллиптический параболоид можно описать как семейство параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх (см. рисунок).
Если
 то
эллиптический параболоид представляет
собой поверхность
вращения,
образованную вращением параболы вокруг
её оси симметрии.
то
эллиптический параболоид представляет
собой поверхность
вращения,
образованную вращением параболы вокруг
её оси симметрии.
Гиперболи́ческий параболо́ид (называемый в строительстве «гипар») — седловая поверхность, описываемая в прямоугольной системе координатуравнением вида
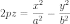 .
.
Также гиперболический параболоид может быть образован движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх (см. рисунок).
Гиперболический параболоид является линейчатой поверхностью.
Цили́ндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Цилиндрическая поверхность — поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть поверхности цилиндра, ограниченная цилиндрической поверхностью, называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями - это основания цилиндра. Таким образом, граница основания будет по форме совпадать с направляющей.В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность и основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии.
Другие виды цилиндра — (по наклону образующей) косой или наклонный (если образующая касается основания не под прямым углом); (по форме основания) эллиптический, гиперболический, параболический.
Призма также является разновидностью цилиндра — с основанием в виде многоугольника.
НА ПЛОСКОСТИ
Уравнение прямой в общем виде имеет вид ax+by+c=0
Если a2+b2=1, то такое уравнение называется нормализованным уравнением прямой.
При этом величина
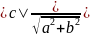 равна расстоянию от данной прямой до
начала координат.
равна расстоянию от данной прямой до
начала координат.
Уравнение в отрезках имеет вид:
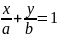
При этом величины a и b равны отрезкам, отсекаемым данной соответственно на осях x и y.
Уравнение прямой, проходящей через точки M1(ч
