Действия с десятичными дробями

1. Сложение и вычитание

Десятичные дроби складывают (вычитают) как целые числа. При этом нужно записывать дроби так, чтобы одинаковые разряды были один под другим.

Примеры: ; ; .

2. Умножение

Десятичные дроби умножают как целые числа (запятую не пишут). В полученном результате отделяют справа запятой столько цифр, сколько их (цифр) было после запятой в сомножителях вместе (в сумме).

Пример: .

Решение. Выполним умножение целых чисел: . В первом сомножителе три цифры после запятой. Во втором сомножителе одна цифра после запятой. Вместе (в сумме) получаем – четыре цифры. В полученном результате отделяем справа запятой четыре цифры и получаем: .

3. Деление

При делении десятичной дроби (или целого числа) на десятичную дробь нужно в делимом и делителе перенести запятую вправо на столько цифр, сколько их (цифр) было после запятой в делителе. Потом выполнить деление на целое число.

Пример 1: .

Решение. В делителе после запятой одна цифра. Перенесем запятую в делителе на одну цифру и выполним деление:

119,2 18	6
	3,2
112 12
0

.

Пример 2: .

Пример 3: .

Слова и словосочетания: десяти́чная дробь, десяти́чная за́пись числа́, коне́чная десяти́чная дробь, бесконе́чная периоди́ческая дробь, разря́д, пери́од, вме́сте; сто́лько…, ско́лько….

Упражнения

1. Прочитайте десятичные дроби:

0,7; 0,19; 1,43; 12,711; 0,003; 31,02; 19,0101; 0,1357; 123,301; 531,0241.

2. Прочитайте периодические дроби. Назовите период дроби:

0,(2); 0,(147); 0,5(6); 1,(901); 15,(4329); 1,8(12); 2,645(73); 12,1(352); 6,23(41).

3. Обратите десятичные дроби в обыкновенные дроби:

А. 0,2; 0,15; 0,375; 0,005; 0,025; 0,105.

Б. 0,205; 0,015; 0,268; 0,0545; 0,1005.

4. Прочитайте дроби, которые можно обратить в конечные десятичные дроби, и обратите эти дроби:

.

5. Выполните вычисления:

а) ;

б) ;

в) ;

г) .

Ответы: 5. а) 1; б) 1; в) 2; г) 1.

Контрольные вопросы

1. Какие части содержит десятичная дробь?

2. Как обратить десятичную дробь в обыкновенную?

3. Как обратить обыкновенную дробь в десятичную?

4. Какие обыкновенные дроби можно обратить в конечные десятичные дроби?

§ 8. Отношения. Пропорции. Проценты

Отношение – это частное от деления числа а на число b, не равное нулю.

или ,

n – это отношение;

a – это предыдущий член отношения;

b – это последующий член отношения.

Отношение читаем так: «отношение а к b равно n».

• Если , то отношение показывает, во сколько раз число а больше, чем число b.

Пример: Во сколько раз 6 больше, чем 3?

Найдем отношение .

6 больше, чем 3 в два раза.

• Если , то отношение показывает, какую часть составляет число а от числа b.

Пример: Какую часть составляет 4 от 12?

Найдем отношение .

4 составляет одну третью часть от 12.

• Если , то .

Пример: Найдите неизвестный член отношения. х – это неизвестный член отношения.

а)  .

б) .

Основное свойство отношения: величина отношения не изменится, если его члены умножить или разделить на одинаковое число, не равное нулю.

Пример: .

Пропорция – это равенство двух отношений: или , .

а и d – это крайние члены пропорции;

b и с – это средние члены пропорции.

Пропорцию читаем так: «а так относится к b, как с относится к d» или «отношение а к b равно отношению с к d».

Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних членов пропорции:

если (a : b = c : d), то .

Чтобы найти неизвестный крайний член пропорции, нужно произведение средних членов разделить на известный крайний член пропорции:

или .

Чтобы найти неизвестный средний член пропорции, нужно произведение крайних членов разделить на известный средний член пропорции:

или .

Примеры: Найти неизвестный член пропорции.

а) , х – это неизвестный средний член пропорции.

.

б) , х – это неизвестный крайний член пропорции.

.

Процент – это сотая часть числа, % – это знак процента.

Читаем проценты так:

1% – один процент (м.р.)

2 % − два

3% − три процента

4% − четыре

5 % − пять

6% − шесть процентов

… …

20% − двадцать

Примеры: 31% – тридцать один процент;

83% – восемьдесят три процента;

97% – девяносто семь процентов;

115% – сто пятнадцать процентов.

Есть три типа задач на проценты:

1. Найти Р% от данного числа А (или найти проценты от числа).

Чтобы найти Р% от данного числа А, нужно это число А разделить на 100 (найти 1% от числа) и умножить на число процентов Р:

Р% от А равны .

Пример: Найти 35% от числа 60.

60 – 100%

х – 35%

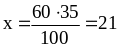
Ответ: 35% от числа 60 равны 21.

2. Найти число, если Р% его равны данному числу B (или найти число по его процентам).

Чтобы найти неизвестное число х по его процентам, нужно данное число В разделить на число процентов Р и умножить на 100:

если Р% от х равны В, то .

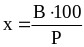Пример: Найти число, если 45% его равны 540.

540 – 45%

х – 100%

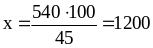
Ответ: число, 45% которого равны 540, составляет 1200.

3. Найти процентное отношение двух чисел.

Чтобы найти процентное отношение двух чисел А и В (узнать, сколько процентов составляет число А от числа В), нужно число А разделить на число В и умножить на 100%.

Процентное отношение А к В равно .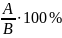

Пример: Найти процентное отношение 14 к 35. (Сколько процентов составляет 14 от 35?).

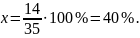
Ответ: процентное отношение 14 к 35 равно 40%. (14 составляет 40% от 35).

Слова и словосочетания: отноше́ние, относи́ться, пропо́рция, проце́нт, зада́ча, найти́, найди́те, составля́ть, пока́зывать, изве́стный, неизве́стный, кра́йний член пропо́рции, сре́дний член пропо́рции, проце́нтное отноше́ние, во ско́лько раз бо́льше, каку́ю часть составля́ет; так…, как… .