Арифметические действия с дробями
Сложение и вычитание дробей
Чтобы сложить (вычесть) дроби с одинаковыми знаменателями, выполняем сложение (вычитание) числителей. Знаменатель не изменяется. Полученную дробь, если можно, сокращаем.
Примеры: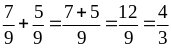
;
.
Чтобы сложить (вычесть) дроби с разными знаменателями, нужно привести дроби к общему (наименьшему) знаменателю, а потом выполнит сложение (вычитание).
Примеры:
;
.
Чтобы сложить (вычесть) смешанные числа, нужно выполнить сложение (вычитание) целых и дробных частей отдельно, а результат записать как смешанное число.
Примеры:
;
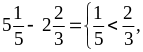тогда
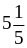запишем как
.
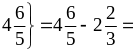
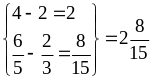Умножение и деление дробей
Чтобы умножить дробь на дробь, нужно числитель умножить на числитель и результат записать в числитель; знаменатель умножить на знаменатель и результат записать в знаменатель. Полученную дробь, если можно, сокращаем.
Пример:
.
Чтобы разделить дробь на дробь, нужно числитель делимого умножить на знаменатель делителя и результат записать в числитель; а знаменатель делимого умножить на числитель делителя и результат записать в знаменатель.
Пример:
.
Чтобы умножить (разделить) смешанные числа, нужно обратить их в неправильные дроби, а потом выполнить умножение (деление).
Примеры:
;
.
Слова и словосочетания: величина́ дро́би, сократи́ть – сокраща́ть, сокраще́ние, сравни́ть – сра́внивать, сравне́ние, сложи́ть, вы́честь, умно́жить, раздели́ть, ра́зный одина́ковый, мо́жно, ну́жно, измени́ть – изменя́ть, преобразова́ть – преобразо́вывать, привести́ – приводи́ть, приведе́ние, приведе́ние дробе́й к о́бщему знамена́телю, дополни́тельный мно́житель, наиме́ньший о́бщий знамена́тель.
Упражнения
1. Сократите дроби:
А.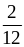
;
;
;
;
;
;
;
;
;
;
;
.
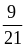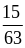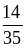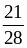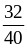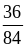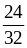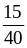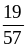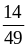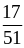Б. 1)
2)
;
3)
4)
.
2. Приведите дроби к общему знаменателю:
А.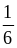
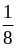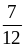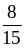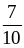и
;
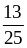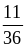и
;
и
;
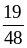и
;
и
.
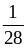Б.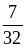
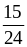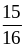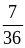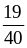и
;
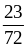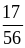и
;
и
;
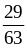и
;
и
.
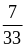3. Сравните дроби:
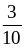и
;
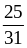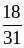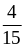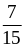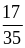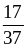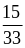и
;
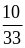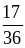и
;
и
;
и
;
и
;
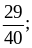
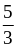и
и
.
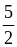4. Выполните вычисления:
а)
б)
в)
г)
Ответы: 4. а) 9; б) 2; в) 2; г) 3.
Контрольные вопросы
1. Какое свойство дроби нужно использовать:
а) чтобы сократить дробь?
б) чтобы привести дроби к общему знаменателю?
2. Как сравнить две дроби:
а) с одинаковыми числителями?
б) с одинаковыми знаменателями?
в) с разными числителями и знаменателями?
3. Как сложить (вычесть) дроби:
а) с одинаковыми знаменателями?
б) с разными знаменателями?
4. Как умножить (разделить) дробь на дробь?
§ 7. Десятичные дроби
Если знаменатель дроби равен 10, или 100, или 1000,…, то такую дробь можно записать как десятичную дробь:
;
;
–
это десятичные дроби.
Запись десятичной дроби содержит целую часть и дробную часть. Сначала пишут целую часть, ставят запятую, потом пишут цифры дробной части. Первая цифра после запятой означает число десятых, вторая – сотых, третья – тысячных и т.д.
Место каждой цифры в десятичной записи числа называется разрядом.
Читают десятичные дроби как смешанные числа.
Пример: 0,1 – ноль целых одна десятая;
0,82 – ноль целых восемьдесят две сотых;
0,019 – ноль целых девятнадцать тысячных;
7,2 – семь целых две десятых;
31,03 – тридцать одна целая три сотых;
500,112 – пятьсот целых сто двенадцать тысячных.
Десятичную дробь можно обратить в обыкновенную дробь
Чтобы обратить десятичную дробь в обыкновенную, нужно записать ее как обыкновенную дробь и, если можно, сократить.
Примеры:
|
|
Обыкновенную дробь можно обратить в десятичную дробь
Чтобы обратить обыкновенную дробь в десятичную, нужно числитель дроби разделить на знаменатель.
1. Если знаменатель содержит только множители 2 и (или) 5, то получится конечная десятичная дробь.
Примеры:
2. Если знаменатель содержит и (или) другие множители, то получится бесконечная десятичная периодическая дробь.
Примеры:
;
.
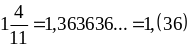Читаем периодические дроби так:
0,(6) – ноль целых шесть в периоде. (6) – это период дроби.
0,8(3) – ноль целых восемь десятых и три в периоде. (3) – это период дроби.
1,(36) – одна целая тридцать шесть в периоде. (36) – это период дроби.
5,2(3) – пять целых две десятых и три в периоде. (3) – это период дроби.