
- •Введение
- •Раздел vі: о. М. Бочарова;
- •Раздел vіі, vііі, іx: п. Г. Бердник.
- •Раздел 1.Начальные сведения
- •§ 1. Цифры и целые числа. Математические знаки
- •Упражнения
- •Контрольные вопросы
- •§ 2. Арифметические действия
- •1. Сложение: 2. Вычитание: 3. Умножение:4. Деление:
- •Порядок арифметических действий
- •Основные законы арифметических действий
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Признаки делимости чисел
- •Упражнения
- •Контрольные вопросы
- •§ 4. Делитель и кратное. Нод и нок
- •Простые и составные числа
- •Наибольший общий делитель (нод)
- •Наименьшее общее кратное (нок)
- •Упражнения
- •Контрольные вопросы
- •§ 5. Обыкновенные дроби
- •Упражнения
- •Контрольные вопросы
- •§ 6. Все действия с дробями
- •Основное свойство дроби
- •Сокращение дробей
- •Приведение дробей к общему (наименьшему) знаменателю
- •Сравнение дробей
- •Арифметические действия с дробями
- •Сложение и вычитание дробей
- •Умножение и деление дробей
- •Упражнения
- •Контрольные вопросы
- •§ 7. Десятичные дроби
- •Действия с десятичными дробями
- •Сложение и вычитание
- •Умножение
- •Деление
- •Упражнения
- •Контрольные вопросы
- •§ 8. Отношения. Пропорции. Проценты
- •Упражнения
- •Контрольные вопросы
- •Раздел 2.Множества. Рациональные числа § 1. Множества
- •Числовые множества
- •Подмножества
- •Действия над множествами
- •Упражнения
- •Контрольные вопросы
- •§ 2. Рациональные числа
- •Противоположные числа
- •Модуль числа
- •Свойства модуля
- •Действия с рациональными числами
- •1. Сравнение рациональных чисел
- •2.Сложение рациональных чисел
- •3. Вычитание рациональных чисел
- •4. Умножение и деление рациональных чисел
- •Алгебраические выражения
- •Упражнения
- •Контрольные вопросы
- •§ 3. Возведение в степень
- •Свойства степени с натуральным показателем
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •Раздел 3.Рациональные выражения
- •§ 1. Одночлены и многочлены
- •Действия над многочленами
- •1.Сложение одночленов и многочленов
- •2. Вычитание одночленов и многочленов
- •Формулы сокращенного умножения
- •Разложение многочленов на множители
- •I.Вынесение общего множителя за скобку
- •II. Группировка членов
- •III.Разложение многочленов на множители с помощью формул сокращенного умножения
- •Упражнения
- •Контрольные вопросы
- •§ 2. Алгебраические дроби
- •Свойства алгебраических дробей
- •Действия с алгебраическими дробями
- •1. Сложение и вычитание алгебраических дробей
- •2. Умножение алгебраических дробей
- •3. Деление алгебраических дробей
- •4. Все действия с алгебраическими дробями
- •Упражнения
- •Контрольные вопросы
- •Раздел 4.Корень. Степень с рациональным показателем
- •§ 1. Корень
- •Иррациональные числа
- •Свойства арифметического корня n– степени
- •Преобразование корней
- •Упражнения
- •Контрольные вопросы
- •§ 2. Подобные корни
- •Действия с корнями
- •1. Сложение и вычитание корней
- •2. Умножение и деление корней
- •3. Возведение корней в степень
- •4. Извлечение корня из корня
- •Упражнения
- •Контрольные вопросы
- •§ 3. Иррациональные выражения
- •Разложение иррациональных выражений на множители
- •Освобождение знаменателя дроби от иррациональности
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 4. Степень с рациональным показателем
- •Основные свойства степени с рациональным показателем
- •Упражнения
- •Контрольные вопросы
- •Раздел 5.Уравнения и системы уравнений первой степени
- •§ 1. Равенства. Тождества. Уравнения
- •Свойства равносильных уравнений
- •Контрольные вопросы
- •§ 2. Линейные уравнения
- •Линейные уравнения с модулем
- •Упражнения
- •Контрольные вопросы
- •§ 3. Системы линейных уравнений с двумя переменными Линейные уравнения с двумя переменными
- •Решение системы двух линейных уравнений с двумя переменными
- •Способ подстановки
- •Способ алгебраического сложения
- •Графический способ
- •Упражнения
- •Контрольные вопросы
- •§ 4. Решение системы двух линейных уравнений с помощью определителей
- •Исследование системы двух линейных уравнений с помощью определителей
- •Раздел 6. Квадратные уравнения и системы уравнений
- •§ 1. Квадратные уравнения
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 2. Теорема виета. Разложение квадратного трёхчлена на множители
- •Разложение квадратного трехчлена на множители
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Биквадратные уравнения и уравнения, приводимые к ним
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 4. Иррациональные уравнения
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Системы нелинейных уравнений с двумя переменными
- •Решение нелинейных систем
- •Метод подстановки
- •II. Метод алгебраического сложения
- •III. Решение системы нелинейных уравнений с двумя переменными с помощью теоремы Виета
- •IV. Решение системы уравнений, которые симметричны относительно х и у
- •V. Решение систем, которые содержат иррациональные выражения
- •Упражнения
- •Контрольные вопросы
- •Раздел 7.Функции
- •§ 1. Функция
- •Способы задания функций
- •Упражнения
- •Контрольные вопросы
- •§ 2. Свойства функции
- •Монотонность функции
- •Четность и нечетность функции
- •Интервалы знакопостоянства
- •Точки пересечения с осями координат
- •Асимптоты
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Линейная функция
- •Прямая пропорциональность
- •Упражнения
- •Контрольные вопросы
- •§ 4. Способы построения графиков функций
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Обратная пропорциональность
- •Упражнения
- •Контрольные вопросы
- •§ 6. Дробно-линейная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 7. Квадратичная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 8. Степенная функция
- •Упражнения
- •Контрольные вопросы
- •Раздел 8. Неравенства
- •§ 1. Числовые неравенства
- •Виды неравенств
- •Свойства числовых неравенств
- •Действия над числовыми неравенствами
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 2. Доказательство неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Неравенства с переменными, системы и совокупности неравенств
- •Свойства равносильных неравенств
- •Контрольные вопросы
- •§ 4. Решение линейных и квадратных неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Решение неравенств методом интервалов
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 6. Решение неравенств, которые содержат переменную под знаком модуля
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 7. Решение иррациональных неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •Раздел 9. Показательная и логарифмическая функции
- •§ 1. Показательная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 2. Показательные уравнения
- •Основные способы решения показательных уравнений
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Показательные неравенства
- •Основные способы решения показательных неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 4. Обратная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Логарифм
- •Свойства логарифмов
- •Теоремы о логарифме произведения, частного и степени
- •Формула перехода к новому основанию
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 6. Логарифмическая функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 7. Логарифмические уравнения
- •Основные способы решения логарифмических уравнений
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 8. Логарифмические неравенства
- •Основные способы решения логарифмических неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •Список литературы
Упражнения
Решите уравнения:
А. 1)
2)
3)
4)
|
5)
6)
7)
|
Б. 1)
2)
3)
4)
5)
6)
7)
8)
|
9)
10)
11)
12) |
B. 1)
2)
3)
4)
5)
6)
7) ; |
8)
9)
10)
11)
12)
13)
14)
|
Ответы: A. 1) 12; 2) 4; 3) 3; 4) – 5 и 1; 5) ; 6) 15; 7) 0,1 и 10.
Б. 1) 0,2
и 125; 2)
;
3) 0,2; 25; 4) 0,01; 100; 5) 0,5 и 8; 6) 100 и
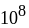 ;
7) 6; 14; 8) 1; 2; 9) 6; 14; 10)
;
7) 6; 14; 8) 1; 2; 9) 6; 14; 10)
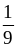 и 9; 11) 2; 12) 3; 13)
и 9.
и 9; 11) 2; 12) 3; 13)
и 9.
B. 1) 2; 2) 1;
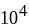 ;
3) 0,1; 10; 4) 10; 5) 10; 6) – 100; – 1; 7) 4;8; 8) 10;
;
3) 0,1; 10; 4) 10; 5) 10; 6) – 100; – 1; 7) 4;8; 8) 10;
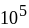 ;
9) 16;
10)
;
9) 16;
10)
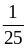 ;
11) 100; 12) 5 и
;
11) 100; 12) 5 и
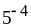 ;
13) 2; 14) 100.
;
13) 2; 14) 100.
Контрольные вопросы
Какое уравнение называется логарифмическим?
Является ли уравнение
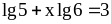 логарифмическим?
логарифмическим?Запишите область определения логарифмического уравнения в виде системы неравенств.
Что такое логарифмирование?
Как решаются показательно-степенные уравнения?
§ 8. Логарифмические неравенства
Логарифмическое неравенство – это неравенство, в котором переменная находится под знаком логарифма или в основании логарифма.
Пример:
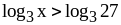 ,
,
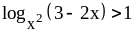 − это логарифмические неравенства.
− это логарифмические неравенства.
Основные способы решения логарифмических неравенств
I. Неравенство
вида
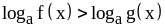 равносильно системе
равносильно системе
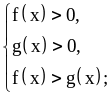 при
или системе
при
или системе
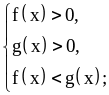 при
.
при
.
II. При
решении неравенств вида
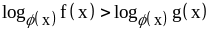 (основание логарифма содержит переменную)
нужно рассмотреть два случая:
и
.
Решение таких неравенств сводится к
решению двух систем:
(основание логарифма содержит переменную)
нужно рассмотреть два случая:
и
.
Решение таких неравенств сводится к
решению двух систем:
а)
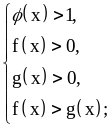 б)
б)
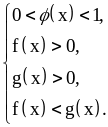
Слова и словосочетания: логарифми́ческое нера́венство.
Упражнения с решениями
Решите неравенство
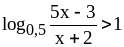 .
.
Решение.
Выразим правую часть
через логарифм:
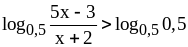 .
Это неравенство равносильно системе:
.
Это неравенство равносильно системе:
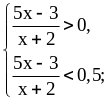
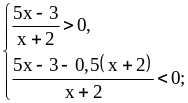
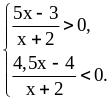
Решение системы показано на рисунке 9.11:
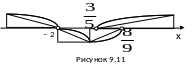
Получим
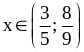 .
.
Ответ: .
Решите неравенство
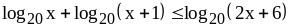 .
.
Решение.
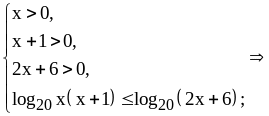
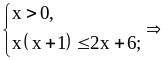
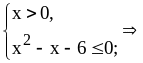
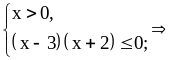
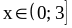 .
.
Ответ: .
Решите неравенство
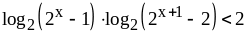 .
.
Решение.
Так как
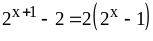 ,
то
,
то
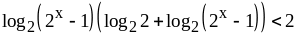
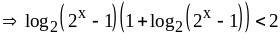 .
.
Пусть
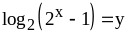 ,
тогда
,
тогда
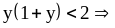
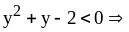
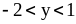 .
Тогда
.
Тогда
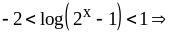
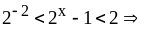
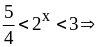
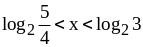 .
.
Ответ:
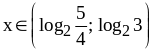 .
.
Решите неравенство
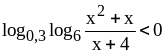 .
.
Решение.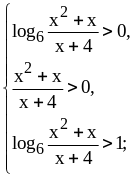
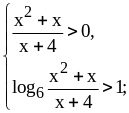
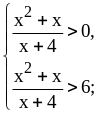
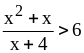
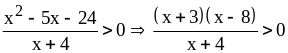
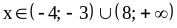 .
.
Ответ: .
Решите неравенство .
Решение. Выразим правую часть через логарифм:
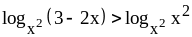 .
.
Решим совокупность двух систем неравенств
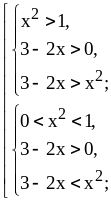
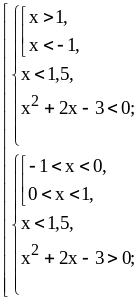
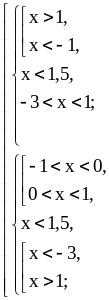 .
.
Ответ:
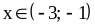 .
.
Упражнения
Решите неравенства:
А. 1)
2)
3)
|
4)
5)
|
Б. 1)
2)
3)
4)
|
5)
6)
7)
8)
|
B. 1)
2)
3)
|
4)
5)
|
Ответы: 1. А.
1) (– 3; 1); 2) (0; 1); 3) (3; 28); 4) (2; 3); 5)
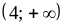 .
.
Б. 1)
 ;
2)
;
2)
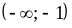 ;
3) (0,5; 3); 4) (0; 3); 5)
;
3) (0,5; 3); 4) (0; 3); 5)
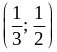 ;
6) (1; 2); 7)
;
6) (1; 2); 7) 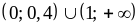 ;
8)
;
8) 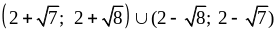 .
.
B. 1)
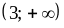 ;
2) (– 1,5; 3),
;
2) (– 1,5; 3),
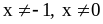 ;
3) (0,1; 100); 4) (0; 1); 5) (– 0,5; 2).
;
3) (0,1; 100); 4) (0; 1); 5) (– 0,5; 2).

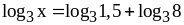 ;
;
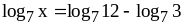 ;
;
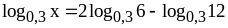 ;
;
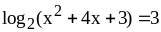 ;
;
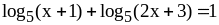 ;
;
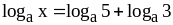 ;
;
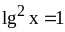 .
.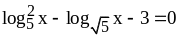 ;
;
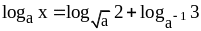 ;
;
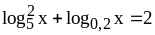 ;
;
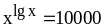 ;
;
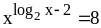 ;
;
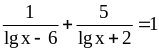 ;
;
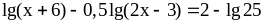 ;
;
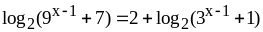 ;
;
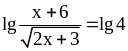 ;
;
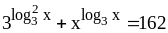 ;
;
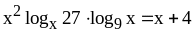 ;
;
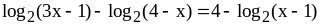 13)
13) 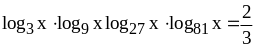 .
.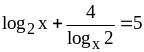 ;
;
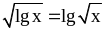 ;
;
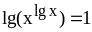 ;
;
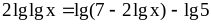 ;
;
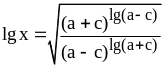 ;
;
 ;
;
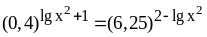 ;
;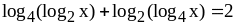 ;
;
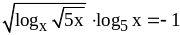 ;
;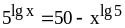 ;
;
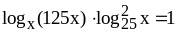 ;
;
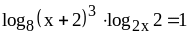 ;
;
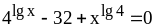 .
.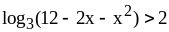 ;
;
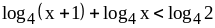 ;
;
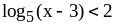 ;
;
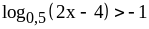 ;
;
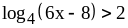 .
.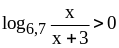 ;
;
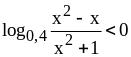 ;
;
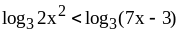 ;
;
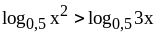 ;
;
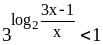 ;
;
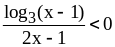 ;
;
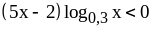 ;
;
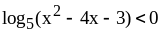 .
.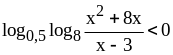 ;
;
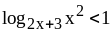 ;
;
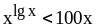 ;
;
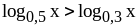 ;
;
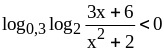 .
.