Наименьшее общее кратное (нок)

Общее кратное двух чисел – это число, которое делится без остатка на каждое из двух чисел.

Пример: найдем общие кратные чисел 6 и 10.

На число 6 делятся числа: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …

На число 10 делятся числа: 10, 20, 30, 40, 50, 60, 70, 80, 90, …

Числа 30, 60, 90, 120, … − это общие кратные чисел 6 и 10.

30 – это наименьшее общее кратное чисел 6 и 10.

Пишем так: НОК(6, 10)=30.

Чтобы найти НОК двух чисел, нужно эти числа разложить на простые множители, выписать все множители и найти их произведение. Общие множители выписываем только один раз.

Пример 1: найдем НОК(6, 10).

Разложим числа 6 и 10 на простые множители и пронумеруем эти множители:

6=2₁∙3₁ 2₁ – это общий множитель;

10=2₁∙5₁ 2₁, 3₁, 5₁ – это все множители.

НОК(6, 10)= 2∙3∙ 5 = 30.

Пример 2: найдем НОК(70, 84).

Разложим числа 70 и 84 на простые множители и пронумеруем эти множители:

70 = 2₁∙5₁∙7₁ 2₁ и 7₁ – это общие множители.

84 = 2₁∙2₂∙3₁∙7₁ НОК(70, 84) = 2∙2∙3∙5∙7 = 420.

НОК двух чисел можно также найти по формуле .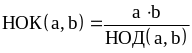

Слова и словосочетания: просто́е число́, составно́е число́, оста́ток, кра́тное (ср.р.), разложи́ть – раскла́дывать, разложе́ние, наибо́льший о́бщий дели́тель (НОД), наиме́ньшее о́бщее кра́тное (НОК).

Упражнения

1. Верно ли, что: а) 5 – делитель числа 45; б) 16 – делитель числа 8; в) 27 – кратное числа 3; г) 6 – кратное числа 12?

2. Из чисел 2, 4, 6, 8, 10, 12, 14, 16 назовите: а) делители числа 20; б) кратные числа 4; в) делители числа 16; г) кратные числа 3.

3. Напишите все делители числа: а) 12; б) 19; в) 27; г) 36.

4. Напишите все двузначные числа, кратные числа: а) 8; б) 11.

5. Назовите однозначные простые числа. Назовите однозначные составные числа.

6. Прочитайте сначала простые числа, а потом составные числа: 5, 8, 9, 12, 13, 14, 17, 19, 21, 23, 25, 29, 31, 36, 42, 45, 47, 49, 51, 62, 67, 77, 83, 90, 91, 95, 97, 101, 109.

7. Разложите числа на простые множители: 27, 36, 46, 72, 84, 100, 243, 368, 420, 1000.

8. а) Разложите на простые множители числа 48 и 64.

б) Назовите все делители числа 48.

в) Назовите все делители числа 64.

г) Назовите общие делители чисел 48 и 64.

д) Назовите НОД чисел 48 и 64.

9. Назовите:

а)все двузначные числа, кратные числа 10.

б) все двузначные числа, кратные числа 15.

в) НОК чисел 10 и 15.

10. Найдите НОД и НОК чисел:

а) 39 и 27; б) 14 и 49; в) 156 и 66; г) 18, 36 и 72;

д) 35, 28 и 56; е) 16, 64 и 96; ё) 12, 18 и 36; ж) 112, 152 и 48.

Контрольные вопросы

1. Что называется делителем числа a?

2. Что называется кратным числа b?

3. Что такое простое число?

4. Что такое составное число?

5. Что такое НОД?

6. Что такое НОК?

§ 5. Обыкновенные дроби

Разделим единицу на равные части (рис. 1.1, 1.2).

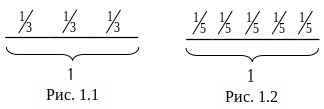
Рисунок 1.1 Рисунок 1.2

На рис. 1.1 единица разделена на 3 равные части: . На рис. 1.2 единица разделена на 5 равных частей: .

Одна часть единицы или несколько равных частей единицы – это обыкновенная дробь.

Пример: – это обыкновенные дроби.

Числитель показывает, сколько равных частей имеет дробь. Знаменатель показывает, на сколько равных частей разделена единица (или на какие равные части разделена единица).

Пример: ­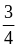– обыкновенная дробь, 3 – числитель, 4 – знаменатель.

Знаменатель 4 показывает: единицу разделили на 4 части. Числитель 3 показывает: дробь имеет 3 таких (четвертых) части.

Обыкновенные дроби читаем так:

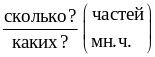или

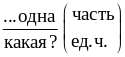
Примеры:

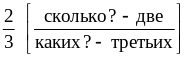– две третьих.

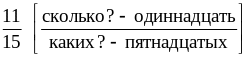− одиннадцать пятнадцатых.

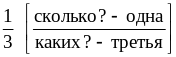− одна третья.

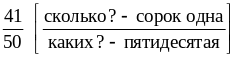− сорок одна пятидесятая.

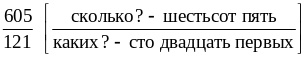− шестьсот пять сто двадцать первых.

Если (числитель меньше, чем знаменатель), то дробь меньше единицы. Это правильная дробь.

Пример: –это правильные дроби.

Если (числитель больше или равен знаменателю), то дробь больше или равна единице. Это неправильная дробь.

Пример: –это неправильные дроби.

Неправильную дробь можно записать как смешанное число.

Говорят: «обратить неправильную дробь в смешанное число».

Пример: Обратим смешанные числа в неправильные дроби: .

Смешанное число имеет целую часть и дробную часть (дробь).

Смешанные числа читаем так:

Примеры:

– одна целая одна вторая;

– двадцать одна целая две третьих;

– две целых три четвертых;

– пятнадцать целых шесть седьмых;

– восемь целых двадцать одна сороковая.

Чтобы обратить неправильную дробь в смешанное число, нужно числитель дроби разделить на знаменатель дроби.

Частное – это будет целая часть смешанного числа.

Пример:Обратить в смешанное число.

	23	5 – это делитель
	20	4 – это частное
	3	− это остаток

Разделим 23 на 5: . .

Смешанное число – это сумма целого числа и дроби.

Смешанное число можно обратить в неправильную дробь.

Пример: .

Чтобы обратить смешанное число в неправильную дробь, нужно сложить целую часть и дробную часть.

Слова и словосочетания: дробь (какая?), обыкнове́нная дробь, пра́вильная дробь, непра́вильная дробь, часть (какая?), це́лая часть, дро́бная часть, о́бщий вид, числи́тель, знамена́тель, черта́ дро́би, ра́вен – равна́ – ра́вный, ско́лько, не́сколько, обрати́ть – обраща́ть, пока́зывать – показа́ть.