
- •Введение
- •Раздел vі: о. М. Бочарова;
- •Раздел vіі, vііі, іx: п. Г. Бердник.
- •Раздел 1.Начальные сведения
- •§ 1. Цифры и целые числа. Математические знаки
- •Упражнения
- •Контрольные вопросы
- •§ 2. Арифметические действия
- •1. Сложение: 2. Вычитание: 3. Умножение:4. Деление:
- •Порядок арифметических действий
- •Основные законы арифметических действий
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Признаки делимости чисел
- •Упражнения
- •Контрольные вопросы
- •§ 4. Делитель и кратное. Нод и нок
- •Простые и составные числа
- •Наибольший общий делитель (нод)
- •Наименьшее общее кратное (нок)
- •Упражнения
- •Контрольные вопросы
- •§ 5. Обыкновенные дроби
- •Упражнения
- •Контрольные вопросы
- •§ 6. Все действия с дробями
- •Основное свойство дроби
- •Сокращение дробей
- •Приведение дробей к общему (наименьшему) знаменателю
- •Сравнение дробей
- •Арифметические действия с дробями
- •Сложение и вычитание дробей
- •Умножение и деление дробей
- •Упражнения
- •Контрольные вопросы
- •§ 7. Десятичные дроби
- •Действия с десятичными дробями
- •Сложение и вычитание
- •Умножение
- •Деление
- •Упражнения
- •Контрольные вопросы
- •§ 8. Отношения. Пропорции. Проценты
- •Упражнения
- •Контрольные вопросы
- •Раздел 2.Множества. Рациональные числа § 1. Множества
- •Числовые множества
- •Подмножества
- •Действия над множествами
- •Упражнения
- •Контрольные вопросы
- •§ 2. Рациональные числа
- •Противоположные числа
- •Модуль числа
- •Свойства модуля
- •Действия с рациональными числами
- •1. Сравнение рациональных чисел
- •2.Сложение рациональных чисел
- •3. Вычитание рациональных чисел
- •4. Умножение и деление рациональных чисел
- •Алгебраические выражения
- •Упражнения
- •Контрольные вопросы
- •§ 3. Возведение в степень
- •Свойства степени с натуральным показателем
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •Раздел 3.Рациональные выражения
- •§ 1. Одночлены и многочлены
- •Действия над многочленами
- •1.Сложение одночленов и многочленов
- •2. Вычитание одночленов и многочленов
- •Формулы сокращенного умножения
- •Разложение многочленов на множители
- •I.Вынесение общего множителя за скобку
- •II. Группировка членов
- •III.Разложение многочленов на множители с помощью формул сокращенного умножения
- •Упражнения
- •Контрольные вопросы
- •§ 2. Алгебраические дроби
- •Свойства алгебраических дробей
- •Действия с алгебраическими дробями
- •1. Сложение и вычитание алгебраических дробей
- •2. Умножение алгебраических дробей
- •3. Деление алгебраических дробей
- •4. Все действия с алгебраическими дробями
- •Упражнения
- •Контрольные вопросы
- •Раздел 4.Корень. Степень с рациональным показателем
- •§ 1. Корень
- •Иррациональные числа
- •Свойства арифметического корня n– степени
- •Преобразование корней
- •Упражнения
- •Контрольные вопросы
- •§ 2. Подобные корни
- •Действия с корнями
- •1. Сложение и вычитание корней
- •2. Умножение и деление корней
- •3. Возведение корней в степень
- •4. Извлечение корня из корня
- •Упражнения
- •Контрольные вопросы
- •§ 3. Иррациональные выражения
- •Разложение иррациональных выражений на множители
- •Освобождение знаменателя дроби от иррациональности
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 4. Степень с рациональным показателем
- •Основные свойства степени с рациональным показателем
- •Упражнения
- •Контрольные вопросы
- •Раздел 5.Уравнения и системы уравнений первой степени
- •§ 1. Равенства. Тождества. Уравнения
- •Свойства равносильных уравнений
- •Контрольные вопросы
- •§ 2. Линейные уравнения
- •Линейные уравнения с модулем
- •Упражнения
- •Контрольные вопросы
- •§ 3. Системы линейных уравнений с двумя переменными Линейные уравнения с двумя переменными
- •Решение системы двух линейных уравнений с двумя переменными
- •Способ подстановки
- •Способ алгебраического сложения
- •Графический способ
- •Упражнения
- •Контрольные вопросы
- •§ 4. Решение системы двух линейных уравнений с помощью определителей
- •Исследование системы двух линейных уравнений с помощью определителей
- •Раздел 6. Квадратные уравнения и системы уравнений
- •§ 1. Квадратные уравнения
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 2. Теорема виета. Разложение квадратного трёхчлена на множители
- •Разложение квадратного трехчлена на множители
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Биквадратные уравнения и уравнения, приводимые к ним
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 4. Иррациональные уравнения
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Системы нелинейных уравнений с двумя переменными
- •Решение нелинейных систем
- •Метод подстановки
- •II. Метод алгебраического сложения
- •III. Решение системы нелинейных уравнений с двумя переменными с помощью теоремы Виета
- •IV. Решение системы уравнений, которые симметричны относительно х и у
- •V. Решение систем, которые содержат иррациональные выражения
- •Упражнения
- •Контрольные вопросы
- •Раздел 7.Функции
- •§ 1. Функция
- •Способы задания функций
- •Упражнения
- •Контрольные вопросы
- •§ 2. Свойства функции
- •Монотонность функции
- •Четность и нечетность функции
- •Интервалы знакопостоянства
- •Точки пересечения с осями координат
- •Асимптоты
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Линейная функция
- •Прямая пропорциональность
- •Упражнения
- •Контрольные вопросы
- •§ 4. Способы построения графиков функций
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Обратная пропорциональность
- •Упражнения
- •Контрольные вопросы
- •§ 6. Дробно-линейная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 7. Квадратичная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 8. Степенная функция
- •Упражнения
- •Контрольные вопросы
- •Раздел 8. Неравенства
- •§ 1. Числовые неравенства
- •Виды неравенств
- •Свойства числовых неравенств
- •Действия над числовыми неравенствами
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 2. Доказательство неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Неравенства с переменными, системы и совокупности неравенств
- •Свойства равносильных неравенств
- •Контрольные вопросы
- •§ 4. Решение линейных и квадратных неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Решение неравенств методом интервалов
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 6. Решение неравенств, которые содержат переменную под знаком модуля
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 7. Решение иррациональных неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •Раздел 9. Показательная и логарифмическая функции
- •§ 1. Показательная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 2. Показательные уравнения
- •Основные способы решения показательных уравнений
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Показательные неравенства
- •Основные способы решения показательных неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 4. Обратная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Логарифм
- •Свойства логарифмов
- •Теоремы о логарифме произведения, частного и степени
- •Формула перехода к новому основанию
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 6. Логарифмическая функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 7. Логарифмические уравнения
- •Основные способы решения логарифмических уравнений
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 8. Логарифмические неравенства
- •Основные способы решения логарифмических неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •Список литературы
§ 6. Решение неравенств, которые содержат переменную под знаком модуля
При решении неравенств, которые содержат переменную под знаком модуля, используют определение модуля выражения
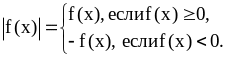
Поэтому неравенство, которое содержит переменную под знаком модуля, равносильно двум системам неравенств:

Решение данного неравенства с модулем – это объединение решений первой и второй систем.
Слова и словосочетания: содержа́ть переме́нную под зна́ком мо́дуля.
Упражнения с решениями
1. Решите
неравенство
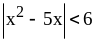 .
.
Решение.
Это неравенство равносильно двум
системам неравенств:
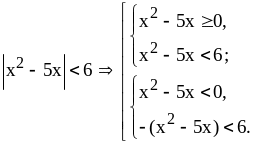 Решим
эти неравенства:
Решим
эти неравенства:
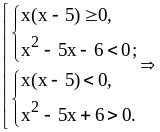
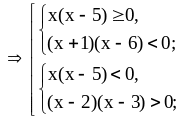
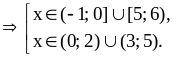
Найдем объединение решений
первой и второй систем:
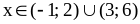 .
.
Ответ: .
2. Решите
неравенство:
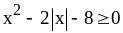 .
.
Решение.
Пусть
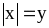 ,
тогда
,
тогда
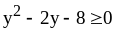 .
Решим это неравенство:
.
Решим это неравенство:
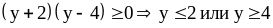 .
.
Получим
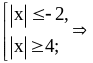
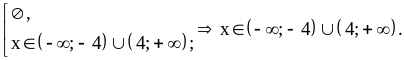
Ответ: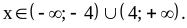
Упражнения
1. Решите неравенства:
А. 1)
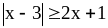 ;
2)
;
2)
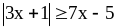 ;
3)
;
3)
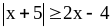 ;
4)
;
4)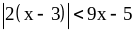 ;
5)
;
5)
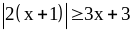 .
.
Б. 1)
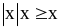 ;
2)
;
2)
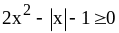 ;
3)
;
3)
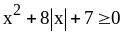 ;
4)
;
4)
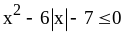 ;
5)
;
5) 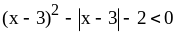 .
.
В. 1) ;
2)
;
2)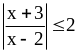 ;
3)
;
4)
;
3)
;
4)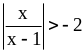 ;
5)
;
5)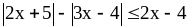 .
.
Ответы. 1. А.
1) 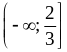 ;
2)
;
2) 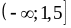 ;
3)
;
3) 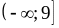 .
4)
;
5)
.
4)
;
5) 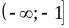 .
.
Б. 1) 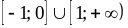 .
2)
.
2) 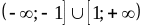 ;
3)
;
4)
;
3)
;
4) 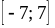 ;
5)
;
5) 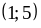 .
В.
1)
.
В.
1) 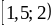 ;
2)
;
2) 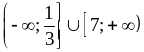 ;
3)
;
3)  ;
4)
;
4) 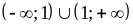 ;
5)
;
5) 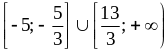 .
.
Контрольные вопросы
Чему равен модуль выражения
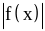 ?
?Каким двум системам неравенств равносильно неравенство, которое содержит переменную под знаком модуля?
§ 7. Решение иррациональных неравенств
Иррациональное неравенство – это неравенство, которое содержит переменную под знаком корня.
Пример:
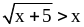 ,
,
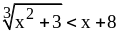 ,
,
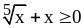 – иррациональные неравенства.
– иррациональные неравенства.
При решении иррациональных неравенств получают одну или несколько систем неравенств. Рассмотрим решение иррациональных неравенств, которые содержат квадратные корни.
Первый
случай.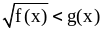 .
.
Это неравенство имеет смысл,
если
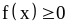 .
Поскольку
.
Поскольку
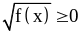 ,
то
,
то
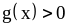 .
Поэтому обе части неравенства можно
возвести в квадрат, т. е. освободиться
от иррациональности. Получим следующую
систему неравенств:
.
Поэтому обе части неравенства можно
возвести в квадрат, т. е. освободиться
от иррациональности. Получим следующую
систему неравенств:
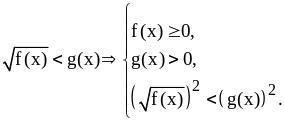
Решение этой системы есть решение данного неравенства.
Второй
случай.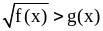 .
.
Это неравенство имеет смысл,
если
.
Правая часть
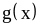 может
иметь положительные значения, отрицательные
значения или может быть равна нулю.
Поэтому:
может
иметь положительные значения, отрицательные
значения или может быть равна нулю.
Поэтому:
а) при
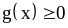 имеем
имеем
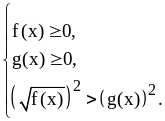
б) при
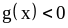 имеем
имеем
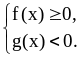
Получим следующую совокупность систем неравенств:
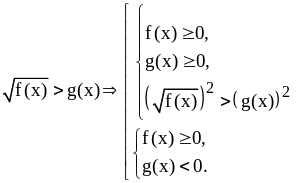
Решение иррационального неравенства есть объединение решений систем а) и б).
Слова и словосочетания: иррациона́льное нера́венство.
Упражнения с решениями
1. Решите
неравенство
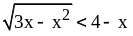 .
.
Решение.
Это иррациональное неравенство
равносильно системе неравенств:
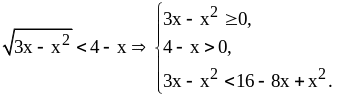
Решим эту систему:
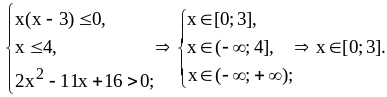
Ответ: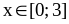 .
.
2. Решите
неравенство
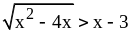 .
.
Решение. Это иррациональное неравенство равносильно совокупности двух систем неравенств:
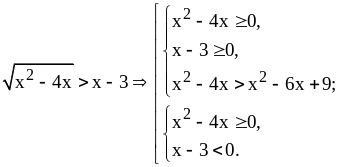
Решим эту совокупность:
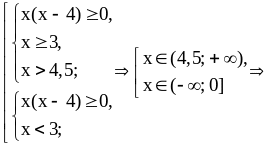
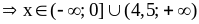 .
.
Ответ: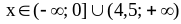 .
.
Упражнения
1. Решите неравенства:
А. 1)
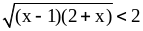 ;
2)
;
2)
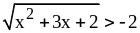 ;
3)
;
3)
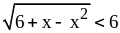 .
.
Б. 1)
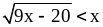 ;
2)
;
2)
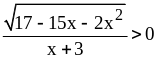 ;
3)
;
3)
 ;
4)
;
4)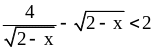 .
.
В. 1)
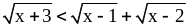 ;
2)
;
2)
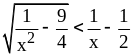 ;
3)
;
3)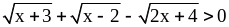 ,
,
2. Решите системы неравенств:
А. 1)
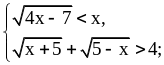 2)
2)
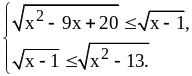
Б. 1)
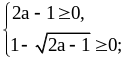 2)
2)
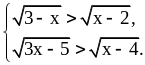
Ответы.
1. А. 1)
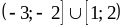 ;
2)
;
2)
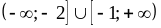 ;
3)
;
3)
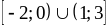 .
.
Б. 1)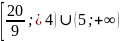 ;
2)
;
2)
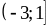 ;
3)
;
3)
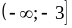 ;
4)
;
4)
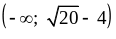 .
.
В. 1)
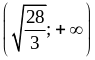 ;
2)
;
2)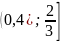 ;
3)
;
3)
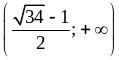 .
.
2. А. 1)
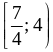 ;
Б. 2)
нет решений.
;
Б. 2)
нет решений.
