
- •Введение
- •Раздел vі: о. М. Бочарова;
- •Раздел vіі, vііі, іx: п. Г. Бердник.
- •Раздел 1.Начальные сведения
- •§ 1. Цифры и целые числа. Математические знаки
- •Упражнения
- •Контрольные вопросы
- •§ 2. Арифметические действия
- •1. Сложение: 2. Вычитание: 3. Умножение:4. Деление:
- •Порядок арифметических действий
- •Основные законы арифметических действий
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Признаки делимости чисел
- •Упражнения
- •Контрольные вопросы
- •§ 4. Делитель и кратное. Нод и нок
- •Простые и составные числа
- •Наибольший общий делитель (нод)
- •Наименьшее общее кратное (нок)
- •Упражнения
- •Контрольные вопросы
- •§ 5. Обыкновенные дроби
- •Упражнения
- •Контрольные вопросы
- •§ 6. Все действия с дробями
- •Основное свойство дроби
- •Сокращение дробей
- •Приведение дробей к общему (наименьшему) знаменателю
- •Сравнение дробей
- •Арифметические действия с дробями
- •Сложение и вычитание дробей
- •Умножение и деление дробей
- •Упражнения
- •Контрольные вопросы
- •§ 7. Десятичные дроби
- •Действия с десятичными дробями
- •Сложение и вычитание
- •Умножение
- •Деление
- •Упражнения
- •Контрольные вопросы
- •§ 8. Отношения. Пропорции. Проценты
- •Упражнения
- •Контрольные вопросы
- •Раздел 2.Множества. Рациональные числа § 1. Множества
- •Числовые множества
- •Подмножества
- •Действия над множествами
- •Упражнения
- •Контрольные вопросы
- •§ 2. Рациональные числа
- •Противоположные числа
- •Модуль числа
- •Свойства модуля
- •Действия с рациональными числами
- •1. Сравнение рациональных чисел
- •2.Сложение рациональных чисел
- •3. Вычитание рациональных чисел
- •4. Умножение и деление рациональных чисел
- •Алгебраические выражения
- •Упражнения
- •Контрольные вопросы
- •§ 3. Возведение в степень
- •Свойства степени с натуральным показателем
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •Раздел 3.Рациональные выражения
- •§ 1. Одночлены и многочлены
- •Действия над многочленами
- •1.Сложение одночленов и многочленов
- •2. Вычитание одночленов и многочленов
- •Формулы сокращенного умножения
- •Разложение многочленов на множители
- •I.Вынесение общего множителя за скобку
- •II. Группировка членов
- •III.Разложение многочленов на множители с помощью формул сокращенного умножения
- •Упражнения
- •Контрольные вопросы
- •§ 2. Алгебраические дроби
- •Свойства алгебраических дробей
- •Действия с алгебраическими дробями
- •1. Сложение и вычитание алгебраических дробей
- •2. Умножение алгебраических дробей
- •3. Деление алгебраических дробей
- •4. Все действия с алгебраическими дробями
- •Упражнения
- •Контрольные вопросы
- •Раздел 4.Корень. Степень с рациональным показателем
- •§ 1. Корень
- •Иррациональные числа
- •Свойства арифметического корня n– степени
- •Преобразование корней
- •Упражнения
- •Контрольные вопросы
- •§ 2. Подобные корни
- •Действия с корнями
- •1. Сложение и вычитание корней
- •2. Умножение и деление корней
- •3. Возведение корней в степень
- •4. Извлечение корня из корня
- •Упражнения
- •Контрольные вопросы
- •§ 3. Иррациональные выражения
- •Разложение иррациональных выражений на множители
- •Освобождение знаменателя дроби от иррациональности
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 4. Степень с рациональным показателем
- •Основные свойства степени с рациональным показателем
- •Упражнения
- •Контрольные вопросы
- •Раздел 5.Уравнения и системы уравнений первой степени
- •§ 1. Равенства. Тождества. Уравнения
- •Свойства равносильных уравнений
- •Контрольные вопросы
- •§ 2. Линейные уравнения
- •Линейные уравнения с модулем
- •Упражнения
- •Контрольные вопросы
- •§ 3. Системы линейных уравнений с двумя переменными Линейные уравнения с двумя переменными
- •Решение системы двух линейных уравнений с двумя переменными
- •Способ подстановки
- •Способ алгебраического сложения
- •Графический способ
- •Упражнения
- •Контрольные вопросы
- •§ 4. Решение системы двух линейных уравнений с помощью определителей
- •Исследование системы двух линейных уравнений с помощью определителей
- •Раздел 6. Квадратные уравнения и системы уравнений
- •§ 1. Квадратные уравнения
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 2. Теорема виета. Разложение квадратного трёхчлена на множители
- •Разложение квадратного трехчлена на множители
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Биквадратные уравнения и уравнения, приводимые к ним
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 4. Иррациональные уравнения
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Системы нелинейных уравнений с двумя переменными
- •Решение нелинейных систем
- •Метод подстановки
- •II. Метод алгебраического сложения
- •III. Решение системы нелинейных уравнений с двумя переменными с помощью теоремы Виета
- •IV. Решение системы уравнений, которые симметричны относительно х и у
- •V. Решение систем, которые содержат иррациональные выражения
- •Упражнения
- •Контрольные вопросы
- •Раздел 7.Функции
- •§ 1. Функция
- •Способы задания функций
- •Упражнения
- •Контрольные вопросы
- •§ 2. Свойства функции
- •Монотонность функции
- •Четность и нечетность функции
- •Интервалы знакопостоянства
- •Точки пересечения с осями координат
- •Асимптоты
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Линейная функция
- •Прямая пропорциональность
- •Упражнения
- •Контрольные вопросы
- •§ 4. Способы построения графиков функций
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Обратная пропорциональность
- •Упражнения
- •Контрольные вопросы
- •§ 6. Дробно-линейная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 7. Квадратичная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 8. Степенная функция
- •Упражнения
- •Контрольные вопросы
- •Раздел 8. Неравенства
- •§ 1. Числовые неравенства
- •Виды неравенств
- •Свойства числовых неравенств
- •Действия над числовыми неравенствами
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 2. Доказательство неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Неравенства с переменными, системы и совокупности неравенств
- •Свойства равносильных неравенств
- •Контрольные вопросы
- •§ 4. Решение линейных и квадратных неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Решение неравенств методом интервалов
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 6. Решение неравенств, которые содержат переменную под знаком модуля
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 7. Решение иррациональных неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •Раздел 9. Показательная и логарифмическая функции
- •§ 1. Показательная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 2. Показательные уравнения
- •Основные способы решения показательных уравнений
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Показательные неравенства
- •Основные способы решения показательных неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 4. Обратная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Логарифм
- •Свойства логарифмов
- •Теоремы о логарифме произведения, частного и степени
- •Формула перехода к новому основанию
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 6. Логарифмическая функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 7. Логарифмические уравнения
- •Основные способы решения логарифмических уравнений
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 8. Логарифмические неравенства
- •Основные способы решения логарифмических неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •Список литературы
Упражнения с решениями
Докажите, что если
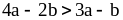 ,
то
.
,
то
.
Доказательство. Найдем разность левой и правой частей этого (данного) неравенства.
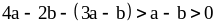 ,
поэтому
.
,
поэтому
.
Выполните сложение неравенств 5 > – 8 и 8 > 5.
Решение.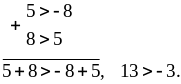
Выполните умножение неравенств 14 > 6 и 2 > 1.
Решение.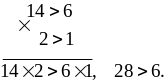
Упражнения
Пусть . Сравните числа:
А. 1) а + х и
b + x; 2) а – 5 и b – 5; 3)
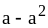 и
и
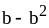 ;
4)
;
4)
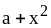 и
и
 .
.
Б. 1)
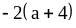 и
и
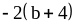 ;
2)
;
2)
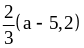 и
и
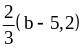 .
.
2. Умножьте обе части неравенства на данное число:
А. 1) 3,25 < 4 на 3; 2) 3,4 > 2,3 на 4; 3) 2а > 1 на 0,5; 4) – 3 < 2 на 2; 5) – 3 < 2 на – 2; 6) – 13 < – 7,5 на – 3.
Б. 1)
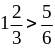 на – 12; 2)
на – 12; 2)
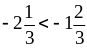 на – 6; 3) – 4а < – 3 на – 0,25;
4)
на – 6; 3) – 4а < – 3 на – 0,25;
4)
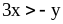 на
на
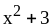 .
.
3. Докажите, что:
В. 1) если
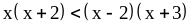 ,
то
,
то
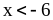 ;
;
2) если
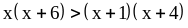 ,
то
,
то
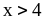 ;
;
3) если
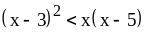 ,
то
,
то
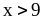 ;
;
4) если
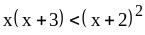 ,
то
,
то
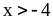 .
.
4. Разделите обе части неравенства на данное число:
А. 1)
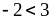 на 3; 2)
на 3; 2)
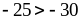 на – 5; 3)
на – 5; 3)
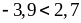 на
на
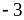 ;
4)
;
4)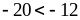 на
.
на
.
Б. 1)
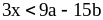 на 3; 2)
на 3; 2)
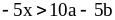 на – 5; 3)
на – 5; 3)
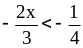 на
на
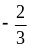 ;
;
4)
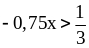 на
на
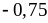 .
.
В. 1)
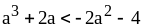 на
на
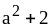 ;
2)
;
2)
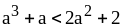 на
на
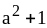 .
.
5. Выполните сложение неравенств:
А. 1)
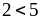 и
и
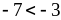 ;
2)
;
2)
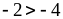 и
и
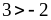 ;
3)
;
3)
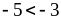 и
и
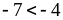 .
.
Б. 1)
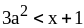 и
и
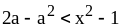 ;
2)
;
2)
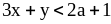 и
и
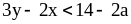 .
.
В. 1)
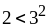 и
и
 ;
2)
;
2)
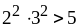 и
и
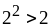 .
.
6. Выполните умножение неравенств:
А. 1)
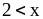 и
и
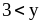 ;
2)
;
2)
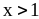 и
и
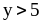 ;
3)
;
3)
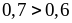 и
и
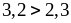 .
.
Б. 1)
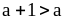 и
и
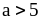 ;
2)
;
2)
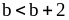 и
и
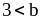 .
.
В. 1)
и
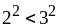 ;
2)
;
2)
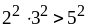 и
;
3)
и
;
3)
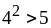 и
и
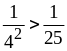 ;
4)
;
4)
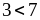 и
и
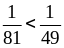 .
.
Контрольные вопросы
Что такое неравенство?
Что такое строгое неравенство?
Что такое нестрогое неравенство?
Что такое неравенства одного знака?
Что такое неравенства противоположного знака?
Что такое числовые неравенства?
Назовите свойства числовых неравенств.
Какие действия можно выполнять над числовыми неравенствами?
§ 2. Доказательство неравенств
Доказать неравенство это значит показать, что оно верное при определенных значениях переменных, которые это неравенство содержит.
При доказательстве неравенств используют несколько способов.
Способ I. Использование определения понятий «больше» и «меньше» (т.е. находят разность между левой и правой частями неравенств).
Пример
1. Докажите, что
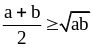 ,
если
,
,
если
,
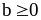 .
.
Доказательство.
Найдем разность между правой и левой
частями неравенства:
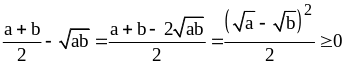 .
.
Следовательно, .
Способ II. Использование известных неравенств.
Пример
2. Докажите, что
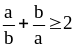 ,
если
,
если
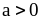 ,
.
,
.
Доказательство.
Так как числа
и
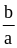 положительны, то
положительны, то
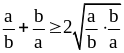 (пример 1), или
.
(пример 1), или
.
Способ III. Использование очевидных (явных) неравенств.
Пример
3. Докажите, что
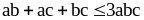 ,
если a, b, с
целые положительные числа.
,
если a, b, с
целые положительные числа.
Доказательство.
Так как а
N, b
N, с
N, то неравенства
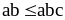 ,
,
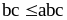 ,
,
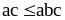 очевидны. Сложим их почленно и получим
.
очевидны. Сложим их почленно и получим
.
Слова и словосочетания: доказа́тельство нера́венств, сле́довательно, очеви́дные нера́венства, очеви́дный = я́вный = легко́ ви́димый.
Упражнения с решениями
1. Докажите
неравенство
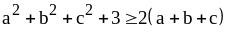 .
.
Доказательство. Найдем разность между правой и левой частями неравенства:
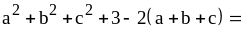
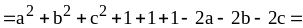
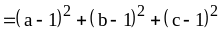 .
.
Выражение
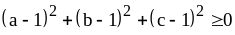 ,
так как сумма неотрицательных чисел
есть число неотрицательное.
,
так как сумма неотрицательных чисел
есть число неотрицательное.
Следовательно, .
2. Докажите
неравенство:
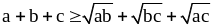 ,
если а, b, с
неотрицательные числа.
,
если а, b, с
неотрицательные числа.
Доказательство.
Используем известные неравенства:
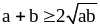 ,
,
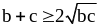 ,
,
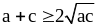 .
Сложим их:
.
Сложим их:
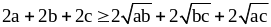 .
Сократим обе части на 2 и получим:
.
.
Сократим обе части на 2 и получим:
.
