Основные законы арифметических действий
Законы сложения
Коммутативный (переместительный) закон: a+b = b+a.
3+5=8 и 5+3=8.
Ассоциативный (сочетательный) закон: (a+b)+с = a+(b+с).
(3+5)+2=8+2=10 и 3+(5+2)=3+7=10.
Законы умножения
Коммутативный (переместительный) закон: a·b = b·a.
3·5=15 и 5·3=15.
Ассоциативный (сочетательный) закон: (a·b)·с = a· (b·с).
(3·5)·2=30 и 3·(5·2)=30.
Дистрибутивный (распределительный) закон: (a+b)·с = a·с+b·с.
Слова и словосочетания: дéйствие, остальны́е, ну́жно, поря́док дéйствий, основно́й; е́сли…, то…; поря́док за́писи, друго́й; снача́ла…, пото́м …; результа́т, заменя́ть (на что?), внутри́, получа́ть результа́т, полу́ченный результа́т, выполня́ть, вну́тренние, испо́льзовать, раскры́ть ско́бки, выраже́ние, содержа́ть.
Упражнения с решениями
1. Прочитайте выражение и выполните действия:
[(324 – 13·12:6+21) – 19]:100+27·2,
раскрываем круглые скобки:
1) умножение: 13·12=156;
2) деление: 156:6= 26;
3) вычитание: 324 – 26=298;
4) сложение: 298+21=319;
раскрываем квадратные скобки:
5) вычитание: 319 – 19=300;
выполняем остальные действия:
6) деление: 300:100=3;
7) умножение: 27·2=54;
8) сложение: 3+54=57.
Упражнения
Прочитайте выражения и выполните действия:
а) 26+2·[(16 – 10) : 3] – 5·4;
б) 10– [(20+8) : 4 +3] : (7 – 2);
в) {125 – [20+(119 – 35 : 7 +6) :8] · 2} : 11 + 5;
г)
.
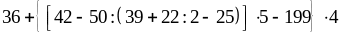Напишите математическими знаками и выполните действия:
а) тридцать минус. Открыть квадратную скобку. Открыть круглую скобку. Двенадцать плюс двадцать. Закрыть круглую скобку. Разделить на восемь, минус два. Закрыть квадратную скобку. Умножить на десять. Равно десяти;
б) двадцать пять минус. Открыть фигурную скобку. Девятнадцать плюс. Открыть квадратную скобку. Двадцать минус. Открыть круглую скобку. Сорок пять разделить на пятнадцать, плюс двенадцать. Закрыть круглую скобку. Плюс семь. Закрыть квадратную скобку. Минус десять. Закрыть фигурную скобку. Будет четыре.
Выполните действия с помощью законов арифметических действий:
-
а)
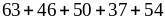;б)
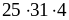;в)
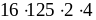;г)
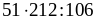;д)
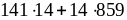;е)
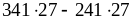;ё)
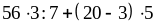;ж)
.
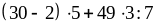Контрольные вопросы
1. Как называются арифметические действия?
2. Как называются результаты арифметических действий?
3. В каком порядке выполняются арифметические действия?
4. Для чего используют скобки в записи арифметических действий?
5. Как вы понимаете слова «раскрыть скобки»?
§ 3. Признаки делимости чисел
Число делится на 2, если его последняя цифра делится на 2.
Пример: числа 22, 30, 546, 4378 делятся на 2, потому что их последние цифры делятся на 2.
Число делится на 5, если его последняя цифра 5 или 0.
Пример: числа 15, 50, 245, 480 делятся на 5, потому что их последние цифры 0 или 5.
Число делится на 3, если сумма его цифр делится на 3.
Пример: число 192 делится на 3, потому что 1+9+2=12, а 12 делится на 3.
Число делится на 9, если сумма его цифр делится на 9.
Пример: число 252 делится на 3, потому что 2+5+2=9, а 9 делится на 9.
Число делится на 10, если его последняя цифра – ноль.
Пример: число 3560 делится на 10, потому что его последняя цифра – ноль.
Число делится на 4, если две его последние цифры делятся на 4.
Пример: число 1972 делится на 4, потому что две его последние цифры – число 72, а 72 делится на 4.
Число делится на 25, если две его последние цифры делятся на 25 или две его последние цифры – нули.
Пример: число 175 делится на 25, потому что две его последние цифры – число 75, а 75 делится на 25; число 2000 делится на 25, потому что две его последние цифры – нули.
Число делится на 8, если три его последние цифры делятся на 8 или три его последние цифры – нули.
Пример: число 3128 делится на 8, потому что три его последние цифры – число 128, а 128 делится на 8; число 2000 делится на 8, потому что три его последние цифры – нули.
Число делится на 125, если три его последние цифры делятся на 125 или три его последние цифры – нули.
Пример: число 1375 делится на 125, потому что три его последние цифры – число 275, а 375 делится на 125; число 2000 делится на 125, потому что три его последние цифры – нули.
Число делится на 6, если оно делится на 2 и 3.
Пример: число 1068, делится на 6, потому что оно делится на 2 (последняя цифра 8) и на 3 (сумма цифр 1+0+6+8=15, а 15 делится на 3).
Слова и словосочетания: при́знак, дели́мость чи́сел, при́знаки дели́мости чи́сел, после́дний, после́дняя ци́фра – после́дние ци́фры, число́ де́лится (на что?).