
- •Введение
- •Раздел vі: о. М. Бочарова;
- •Раздел vіі, vііі, іx: п. Г. Бердник.
- •Раздел 1.Начальные сведения
- •§ 1. Цифры и целые числа. Математические знаки
- •Упражнения
- •Контрольные вопросы
- •§ 2. Арифметические действия
- •1. Сложение: 2. Вычитание: 3. Умножение:4. Деление:
- •Порядок арифметических действий
- •Основные законы арифметических действий
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Признаки делимости чисел
- •Упражнения
- •Контрольные вопросы
- •§ 4. Делитель и кратное. Нод и нок
- •Простые и составные числа
- •Наибольший общий делитель (нод)
- •Наименьшее общее кратное (нок)
- •Упражнения
- •Контрольные вопросы
- •§ 5. Обыкновенные дроби
- •Упражнения
- •Контрольные вопросы
- •§ 6. Все действия с дробями
- •Основное свойство дроби
- •Сокращение дробей
- •Приведение дробей к общему (наименьшему) знаменателю
- •Сравнение дробей
- •Арифметические действия с дробями
- •Сложение и вычитание дробей
- •Умножение и деление дробей
- •Упражнения
- •Контрольные вопросы
- •§ 7. Десятичные дроби
- •Действия с десятичными дробями
- •Сложение и вычитание
- •Умножение
- •Деление
- •Упражнения
- •Контрольные вопросы
- •§ 8. Отношения. Пропорции. Проценты
- •Упражнения
- •Контрольные вопросы
- •Раздел 2.Множества. Рациональные числа § 1. Множества
- •Числовые множества
- •Подмножества
- •Действия над множествами
- •Упражнения
- •Контрольные вопросы
- •§ 2. Рациональные числа
- •Противоположные числа
- •Модуль числа
- •Свойства модуля
- •Действия с рациональными числами
- •1. Сравнение рациональных чисел
- •2.Сложение рациональных чисел
- •3. Вычитание рациональных чисел
- •4. Умножение и деление рациональных чисел
- •Алгебраические выражения
- •Упражнения
- •Контрольные вопросы
- •§ 3. Возведение в степень
- •Свойства степени с натуральным показателем
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •Раздел 3.Рациональные выражения
- •§ 1. Одночлены и многочлены
- •Действия над многочленами
- •1.Сложение одночленов и многочленов
- •2. Вычитание одночленов и многочленов
- •Формулы сокращенного умножения
- •Разложение многочленов на множители
- •I.Вынесение общего множителя за скобку
- •II. Группировка членов
- •III.Разложение многочленов на множители с помощью формул сокращенного умножения
- •Упражнения
- •Контрольные вопросы
- •§ 2. Алгебраические дроби
- •Свойства алгебраических дробей
- •Действия с алгебраическими дробями
- •1. Сложение и вычитание алгебраических дробей
- •2. Умножение алгебраических дробей
- •3. Деление алгебраических дробей
- •4. Все действия с алгебраическими дробями
- •Упражнения
- •Контрольные вопросы
- •Раздел 4.Корень. Степень с рациональным показателем
- •§ 1. Корень
- •Иррациональные числа
- •Свойства арифметического корня n– степени
- •Преобразование корней
- •Упражнения
- •Контрольные вопросы
- •§ 2. Подобные корни
- •Действия с корнями
- •1. Сложение и вычитание корней
- •2. Умножение и деление корней
- •3. Возведение корней в степень
- •4. Извлечение корня из корня
- •Упражнения
- •Контрольные вопросы
- •§ 3. Иррациональные выражения
- •Разложение иррациональных выражений на множители
- •Освобождение знаменателя дроби от иррациональности
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 4. Степень с рациональным показателем
- •Основные свойства степени с рациональным показателем
- •Упражнения
- •Контрольные вопросы
- •Раздел 5.Уравнения и системы уравнений первой степени
- •§ 1. Равенства. Тождества. Уравнения
- •Свойства равносильных уравнений
- •Контрольные вопросы
- •§ 2. Линейные уравнения
- •Линейные уравнения с модулем
- •Упражнения
- •Контрольные вопросы
- •§ 3. Системы линейных уравнений с двумя переменными Линейные уравнения с двумя переменными
- •Решение системы двух линейных уравнений с двумя переменными
- •Способ подстановки
- •Способ алгебраического сложения
- •Графический способ
- •Упражнения
- •Контрольные вопросы
- •§ 4. Решение системы двух линейных уравнений с помощью определителей
- •Исследование системы двух линейных уравнений с помощью определителей
- •Раздел 6. Квадратные уравнения и системы уравнений
- •§ 1. Квадратные уравнения
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 2. Теорема виета. Разложение квадратного трёхчлена на множители
- •Разложение квадратного трехчлена на множители
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Биквадратные уравнения и уравнения, приводимые к ним
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 4. Иррациональные уравнения
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Системы нелинейных уравнений с двумя переменными
- •Решение нелинейных систем
- •Метод подстановки
- •II. Метод алгебраического сложения
- •III. Решение системы нелинейных уравнений с двумя переменными с помощью теоремы Виета
- •IV. Решение системы уравнений, которые симметричны относительно х и у
- •V. Решение систем, которые содержат иррациональные выражения
- •Упражнения
- •Контрольные вопросы
- •Раздел 7.Функции
- •§ 1. Функция
- •Способы задания функций
- •Упражнения
- •Контрольные вопросы
- •§ 2. Свойства функции
- •Монотонность функции
- •Четность и нечетность функции
- •Интервалы знакопостоянства
- •Точки пересечения с осями координат
- •Асимптоты
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Линейная функция
- •Прямая пропорциональность
- •Упражнения
- •Контрольные вопросы
- •§ 4. Способы построения графиков функций
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Обратная пропорциональность
- •Упражнения
- •Контрольные вопросы
- •§ 6. Дробно-линейная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 7. Квадратичная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 8. Степенная функция
- •Упражнения
- •Контрольные вопросы
- •Раздел 8. Неравенства
- •§ 1. Числовые неравенства
- •Виды неравенств
- •Свойства числовых неравенств
- •Действия над числовыми неравенствами
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 2. Доказательство неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Неравенства с переменными, системы и совокупности неравенств
- •Свойства равносильных неравенств
- •Контрольные вопросы
- •§ 4. Решение линейных и квадратных неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Решение неравенств методом интервалов
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 6. Решение неравенств, которые содержат переменную под знаком модуля
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 7. Решение иррациональных неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •Раздел 9. Показательная и логарифмическая функции
- •§ 1. Показательная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 2. Показательные уравнения
- •Основные способы решения показательных уравнений
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 3. Показательные неравенства
- •Основные способы решения показательных неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 4. Обратная функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 5. Логарифм
- •Свойства логарифмов
- •Теоремы о логарифме произведения, частного и степени
- •Формула перехода к новому основанию
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 6. Логарифмическая функция
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 7. Логарифмические уравнения
- •Основные способы решения логарифмических уравнений
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •§ 8. Логарифмические неравенства
- •Основные способы решения логарифмических неравенств
- •Упражнения с решениями
- •Упражнения
- •Контрольные вопросы
- •Список литературы
Разложение многочленов на множители
Разложить многочлен на множители – это значит записать его как произведение нескольких множителей.
Есть три основных способа разложения многочленов на множители.
I.Вынесение общего множителя за скобку
Пример 1: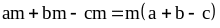 .
.
Здесь m – общий множитель, который вынесли за скобку. Чтобы узнать, что написать в скобках, необходимо разделить каждый член многочлена на общий множитель и результат записать в скобках.
Пример 2: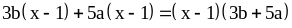 .
.
Здесь общий множитель x– 1.
Пример 3: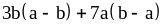 .
.
Здесь общего множителя нет.
Изменим знак перед второй скобкой и в
скобке. Получим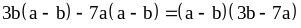 .
.
Пример 4: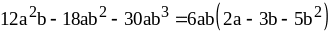 .
.
II. Группировка членов
Рассмотрим примеры.
Пример 1:Разложить
на множители многочлен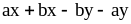 .
.
Члены этого многочлена не имеют общего множителя. Сгруппируем члены так, чтобы эти группы членов имели общий множитель:
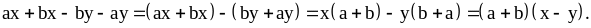 Примечание.
Сгруппировать члены можно и по– другому:
Примечание.
Сгруппировать члены можно и по– другому:
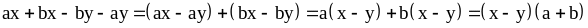 .
Видно, что результаты одинаковые.
.
Видно, что результаты одинаковые.
Пример 2: Разложить на множители многочлен
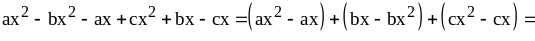
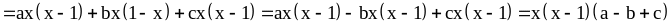
III.Разложение многочленов на множители с помощью формул сокращенного умножения
Напишем формулы сокращенного умножения справа налево. Получим формулы разложения многочленов на множители:
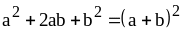 , (1)
, (1)
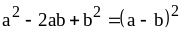 , (2)
, (2)
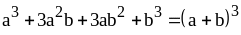 , (3)
, (3)
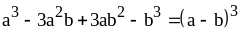 , (4)
, (4)
, (5)
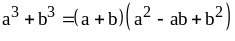 , (6)
, (6)
, (7).
Формулу (5) читаем так: разность квадратов раскладывается на разность и сумму оснований.
Формулу (6) читаем так: сумма кубов раскладывается на сумму оснований и неполный квадрат разности.
Формулу (7) читаем так: разность кубов раскладывается на разность оснований и неполный квадрат суммы.
Рассмотрим примеры:
Пример 1: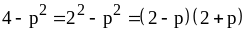 .
.
Пример 2: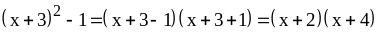 .
.
Пример 3: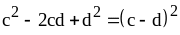 .
.
Пример 4: .
.
Пример 5: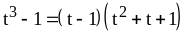 .
.
Пример 6: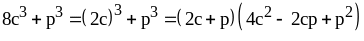 .
.
Новые слова и выражения: одночле́н(– ы), многочле́н(– ы), отлича́ться (чем? от чего?), подо́бный (– ая, – ое, – ые), приводи́ть (что? к чему?), привести́ (что? к чему?), приведе́ние (чего?), припи́сывать (что? к чему?), приписа́ть (что? к чему?), опуска́ть (что?), опусти́ть (что?), заключа́ть (что?), заключи́ть (что?), изменя́ть (что?), измени́ть (что?), сократи́ть, сокраща́ть (что?), сокращё́нный (– ая, – ое, – ые), удво́ить (что?), удво́енный (– ая, – ое, – ые), утро́ить (что?), утро́енный (– ая, – ое, – ые), непо́лный (– ая, – ое, – ые), разлага́ть (что? на что?), разложи́ть (что? на что?), разложе́ние, выноси́ть (что? куда?), вы́нести (что? куда?), вынесе́ние, группирова́ть (что?), сгруппирова́ть (что? с чем?), группиро́вка.
Упражнения
А
1. Приведите подобные слагаемые:
1)
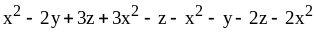 ;
;
2)
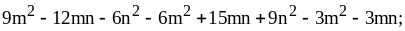
3)
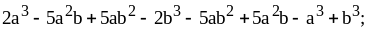
4)
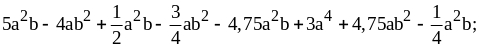
5)
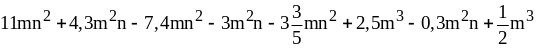 .
.
2. Раскройте скобки и приведите подобные слагаемые:
1)
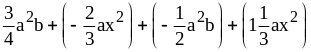 ;
;
2)
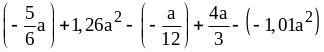 ;
;
3)
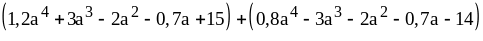 ;
;
4)
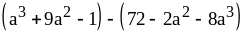 ;
;
5)
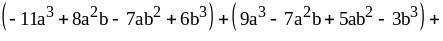
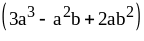 ;
;
6)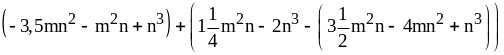 ;
;
7)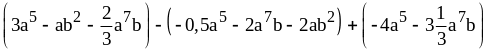 ;
;
8)
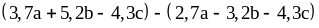 ;
;
9)
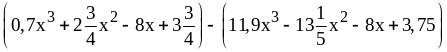 ;
;
10)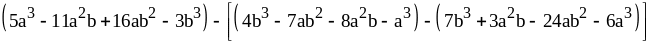
3. Выполните умножение:
1)
2)
3)
4)
5) |
6)
7)
8)
9)
10)
|
4. Выполните деление:
1)
2)
3)
4)
|
5)
6)
7)
8)
|
5. Возведите одночлены в степень:
1)
2)
|
3)
4)
5)
|
6. Упростите выражение и найдите его числовое значение:
1)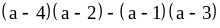 при
при
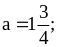
2)
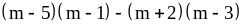 при
при
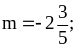
3)
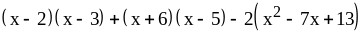 при
при
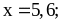
4)
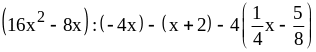 при
при
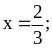
5)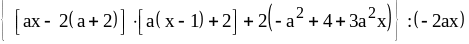 ,
,
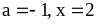 .
.
7. Разделить многочлен на одночлен:
1)
/2)
3)
4)
|
5)
6)
7)
|
8. Разделите многочлен на многочлен:
1)
2)
3)
4)
5)
|
6)
7)
8)
9)
10)
|
9. Выполните действия с помощью формул сокращенного умножения:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
|
21)
22)
23)
24)
25)
26)
27)
28)
29)
30)
31)
32)
33)
34)
35)
36)
|
10. Выполните действия:
1)
2)
3)
4)
|
5)
6)
7)
|
11. Разложите на множители методом вынесения общих множителей за скобку:
1)
2)
3)
4)
5)
6)
7)
8)
9)
|
10)
11)
12)
13)
14)
15)
16)
17)
|
12. Решите уравнения способом разложения на множители левой части уравнения:
1)
2)
|
3)
4)
|
13. Разложите многочлены на множители способом группировки:
1)
2)
3)
4)
5)
6)
7)
|
8)
9)
10)
11)
12)
13)
14)
|
14. Разложите многочлены на множители по формулам сокращенного умножения:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
|
18)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)
29)
30)
31)
32)
33)
|
15. Разложите на множители:
1)
2)
3)
4)
5)
6)
|
7)
8)
9)
10)
11)
12)
|
Б
1. Сложите многочлены:
1)
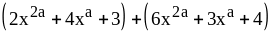 ;
;
2)
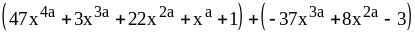 .
.
2. Вычесть многочлены:
1)
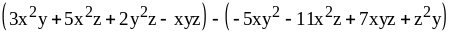 ;
;
2)
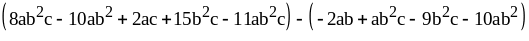 ;
;
3)
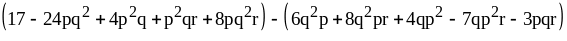 .
.
3. Выполнить умножение:
1)
2)
3)
4)
5)
6)
7)
8)
|
9)
10)
11)
12)
13)
14)
15)
16)
17)
|
4. Выполните деление:
1)
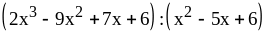 ;
;
2)
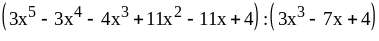 ;
;
3)
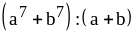 ;
;
4)
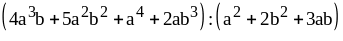 ;
;
5)
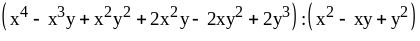 .
.
5. Разложите на множители:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
|
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
23)
24)
|
6. Найдите числовые значения выражений (сначала разложите их на множители):
1)
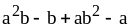 при
при
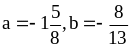 ;
;
2)
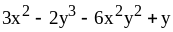 при
при
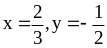 .
.
7. Выполните деление (сначала разложите делимое и делитель на множители):
1)
2)
|
3)
4)
|
5)
6)
|
Ответы: А.
2. 3)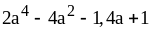 ;
5)
;
5) ;
7)
;
7)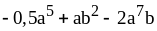 ;
9)
;
9)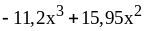 ;
10)
;
10)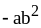 .
.
3. 1)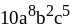 ;
3)
;
3)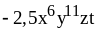 ;
5)
;
5)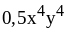 ;
7)
;
7)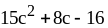 ;
9)
;
9)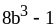 .
.
4. 1)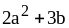 ;3)
;3)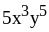 ;
5)
;
5)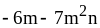 ;
7)
;
7)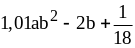 .
.
5. 1)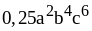 ;
3)
;
3)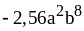 ;
5)
;
5)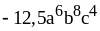 .
.
6. 1) 1,5; 3)
6; 5)
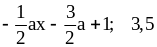 .
.
7. 1)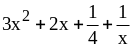 ;
3)
;
3)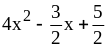 ;
5)
;
5)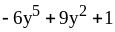 ;
7)
;
7) 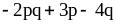 .
.
8. 1)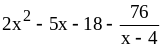 ;
3)
;
3)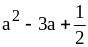 ;
5)
;
5)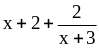 ;
7)
;
7)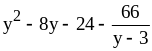 ;
9)
;
9)
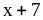 .
.
9. 17)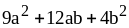 ;
19)
;
19)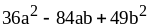 ;
21)
;
21)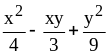 ;
23)
;
23)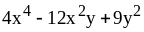 ;
25)
;
25)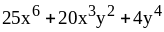 ;
27)
;
27)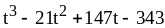 ;
29)
;
29)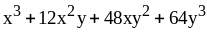 ;
31)
;
31)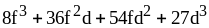 ;
;
10. 1)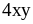 ;
3)
;
3)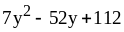 ;
5)
;
5)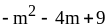 ;
7)
;
7)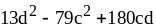 ;
;
11. 9)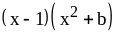 ;
11)
;
11)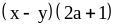 ;
13)
;
13) ;
15)
;
15)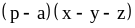 .
.
12. 1)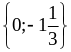 ;
3)
;
3)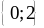 .
.
13. 1)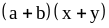 ;
3)
;
3)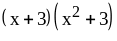 ;
5)
;
5) ;
7)
;
7)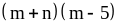 ;
9)
;
9)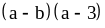 ;
11)
;
11)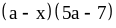 ;
13)
;
13)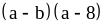 .
.
14. 15)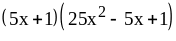 ;
17)
;
17)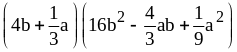 ;
25)
;
25)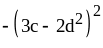 ;
27)
;
27)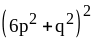 ;
29)
;
29)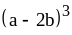 ;
31)
;
31)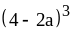 ;
33)
;
33)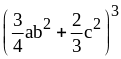 .
.
15. 7)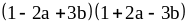 ;
9)
;
9)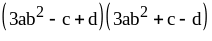 ;
11)
;
11)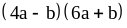 .
.
Б.
1. 1)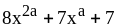 ;
2)
;
2)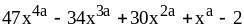 .
.
2. 1)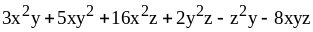 ;
3)
;
3)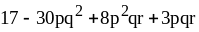 .
.
3. 1)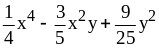 ;
3)
;
3)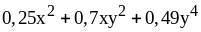 ;
5)
;
5)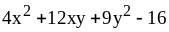 ;
7)
;
7)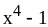 ;
9)
;
9)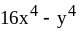 ;
11)
;
11)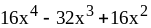 ;
13)
;
13)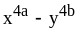 ;
15)
;
17)
;
15)
;
17)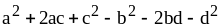 .
.
4. 1)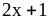 ;
3)
;
3)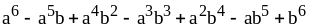 ;
5)
;
5)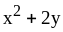 .
.
5. 1)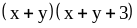 ;
3)
;
3)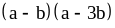 ;
5)
;
5)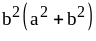 ;
7)
;
7)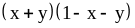 ;
9)
;
9)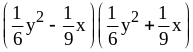 ;
11)
;
11)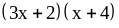 ;
13)
;
13)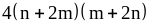 ;
15)
;
15)![]() ;
17)
;
17)![]() ;
19)
;
19)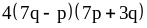 ;
21)
;
21)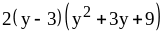 ;
23)
;
23)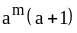 .
.
6. 1) 0; 2)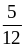 .
7. 1)
.
7. 1)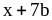 ;
3)
;
3)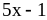 ;
5)
;
5)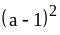 .
.

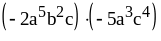 ;
;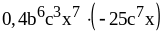 ;
;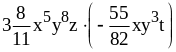 ;
;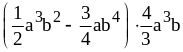 ;
;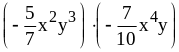 ;
;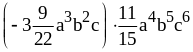 ;
;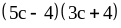 ;
;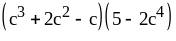 ;
;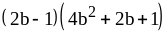 ;
;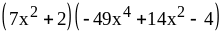 .
.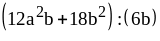 ;
;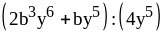 ;
;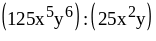 ;
;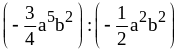 ;
;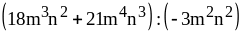 ;
;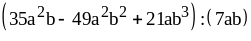 ;
;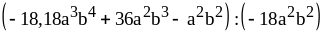 ;
;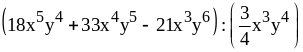 .
.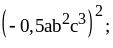
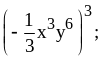
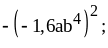
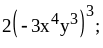
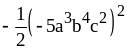 .
.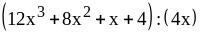 ;
;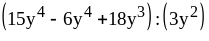 ;
;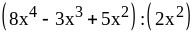 ;
;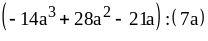 ;
;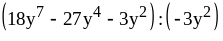 ;
;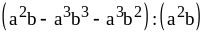 ;
;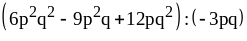 .
.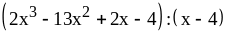 ;
;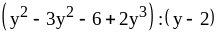 ;
;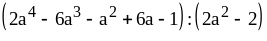 ;
;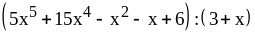 ;
;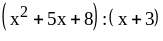 ;
;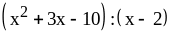 ;
;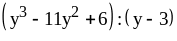 ;
;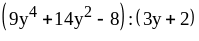 ;
;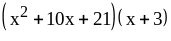 ;
;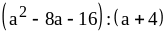 .
.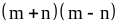 ;
; 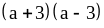 ;
;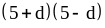 ;
;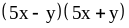 ;
;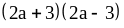 ;
;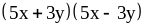 ;
;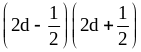 ;
;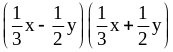 ;
;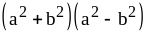 ;
;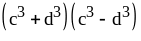 ;
; ;
;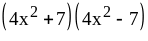 ;
;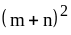 ;
;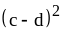 ;
;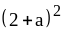 ;
;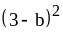 ;
; ;
;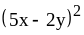 ;
;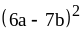 ;
;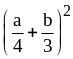 ;
;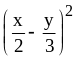 ;
;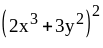 ;
;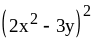 ;
;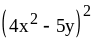 ;
;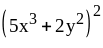 ;
;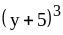 ;
;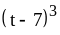 ;
; 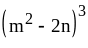 ;
;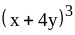 ;
;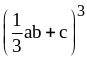 ;
;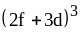 ;
;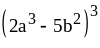 ;
;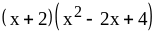 ;
;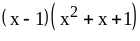 ;
; ;
;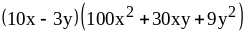 .
.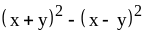 ;
;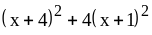 ;
;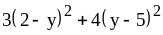 ;
;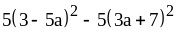 ;
;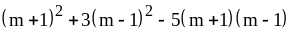 ;
;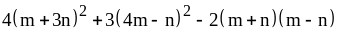 ;
;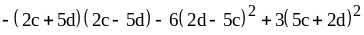 .
.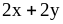 ;
;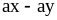 ;
;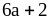 ;
;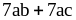 ;
;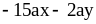 ;
;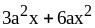 ;
;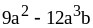 ;
;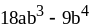 ;
;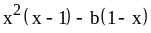 ;
;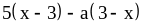 ;
;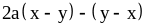 ;
;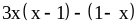 ;
;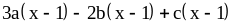 ;
;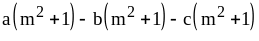 ;
;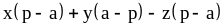 ;
;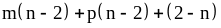 ;
;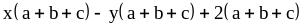 .
.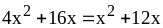 ;
;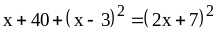 ;
;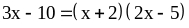 ;
;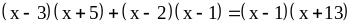 .
.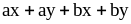 ;
;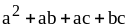 ;
;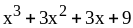 ;
;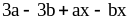 ;
;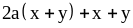 ;
;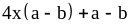 ;
;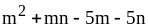 ;
; ;
;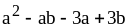 ;
;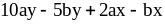 ;
;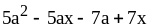 ;
; 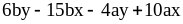 ;
;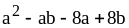 ;
;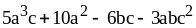 .
.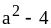 ;
;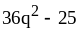 ;
;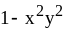 ;
; 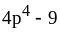 ;
;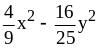 ;
;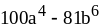 ;
;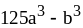 ;
; ;
;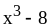 ;
;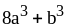 ;
;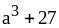 ;
;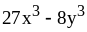 ;
; ;
; 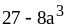 ;
;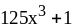 ;
; ;
;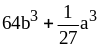 ;
;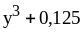 ;
;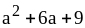 ;
;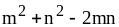 ;
;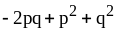 ;
;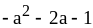 ;
;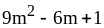 ;
; 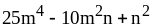 ;
;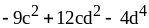 ;
;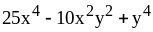 ;
;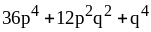 ;
; 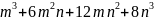 ;
;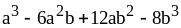 ;
;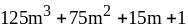 ;
;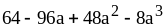 ;
;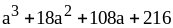 ;
;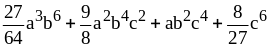 .
.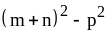 ;
;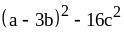 ;
;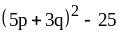 ;
;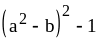 ;
; ;
;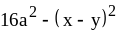 ;
;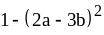 ;
;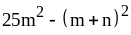 ;
;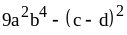 ;
;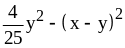 ;
;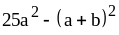 ;
;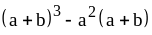 .
. ;
;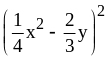 ;
;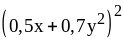 ;
;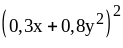 ;
;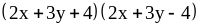 ;
;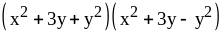 ;
;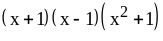 ;
;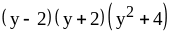 ;
;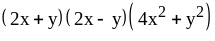 ;
;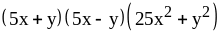 ;
;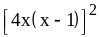 ;
;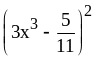 ;
;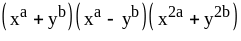 ;
;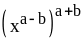 ;
;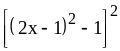 ;
;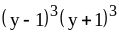 ;
;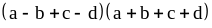 .
.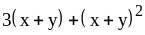 ;
;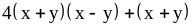 ;
;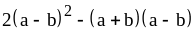 ;
;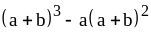 ;
;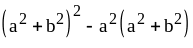 ;
;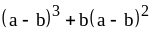 ;
;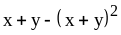 ;
;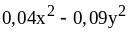 ;
;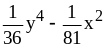 ;
;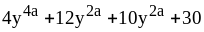 ;
;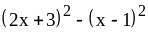 ;
;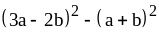 ;
;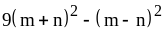 ;
;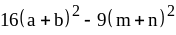 ;
;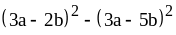 ;
;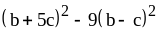 ;
;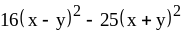 ;
; ;
;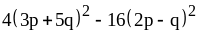 ;
;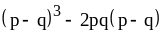 ;
;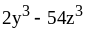 ;
;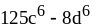 ;
;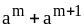 ;
;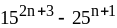 .
.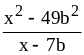 ;
;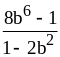 ;
;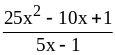 ;
; 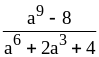 ;
;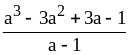 ;
;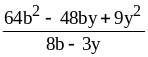 .
.