3.2 Задания на самостоятельную подготовку
Задача 3.1
Определить матричную передаточную функцию системы, описываемой следующими дифференциальными уравнениями:
а)
б)
в)
г)
д)
е)
ж)
з)
и)
к)
Задача 2.2
Определить матричную передаточную функцию, если известны матрицы А, В и С:
а)
,
,
;
б)
,
,
;
в)
,
,
;
г)
,
,
;
д)
,
,
;
е)
,
,
;
ж)
,
,
;
з)
,
,
;
и)
,
,
;
к)
,
,
;
2.1 Первая каноническая форма
Для получения первой канонической формы системы, с передаточной функцией (1.1), необходимо:
Представить структурную схему в виде двух последовательных звеньев, соответствующих уравнению (2.5) , обозначив переход через z (рисунок 2.2);
Рисунок 2.2. Структурное представление системы, соответствующее уравнению (2.5).
Для каждого звена системы записать соответствующие операторные уравнения:
(2.7)
Определить старшую производную переменной z из первого уравнения (2.7), что соответствует значению
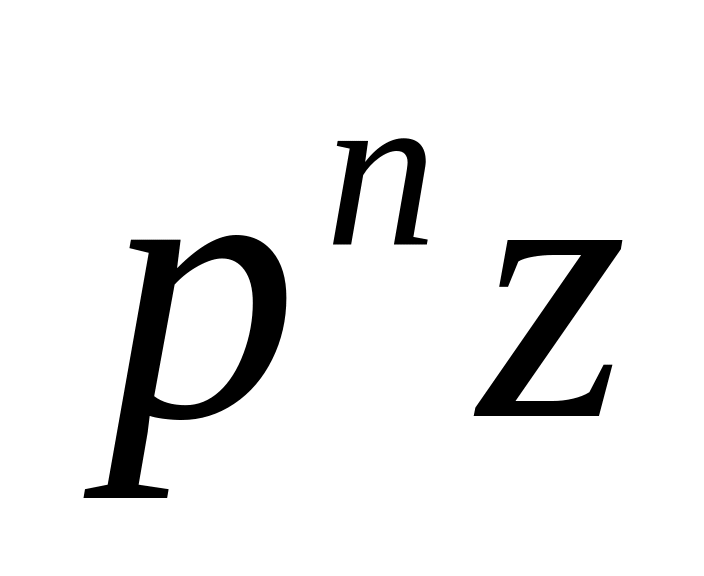в операторной форме:
(2.8)
Представить (2.8) в виде цепочки из k интеграторов (рисунок 2.3), где n – порядок системы, и добавить выходную переменную y в соответствии со вторым уравнением (2.7);
Рисунок 2.2. Структурная схема, соответствующая первой канонической форме
От полученной структурной схемы перейти к модели системы в переменных состояния в виде (2.9), обозначив выход каждого интегратора за переменную состояния
,
,
…,
;
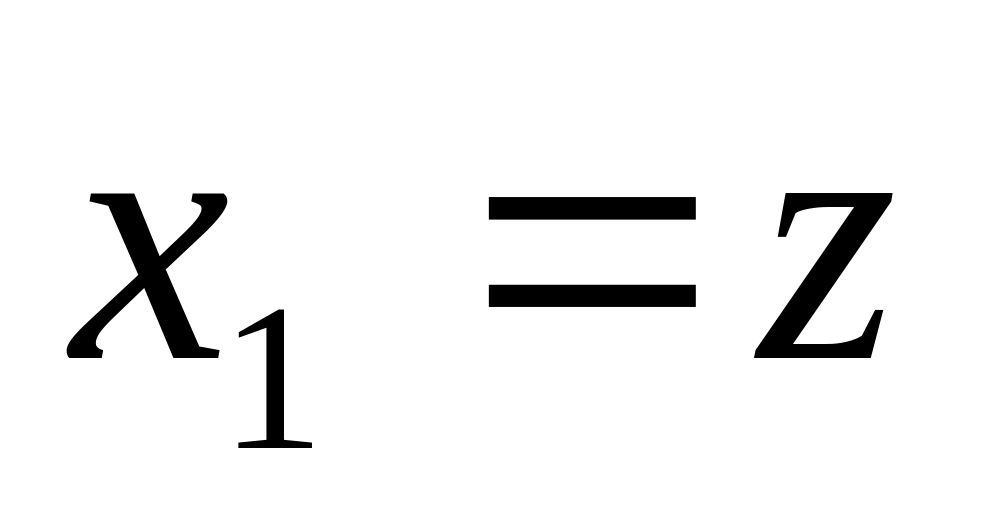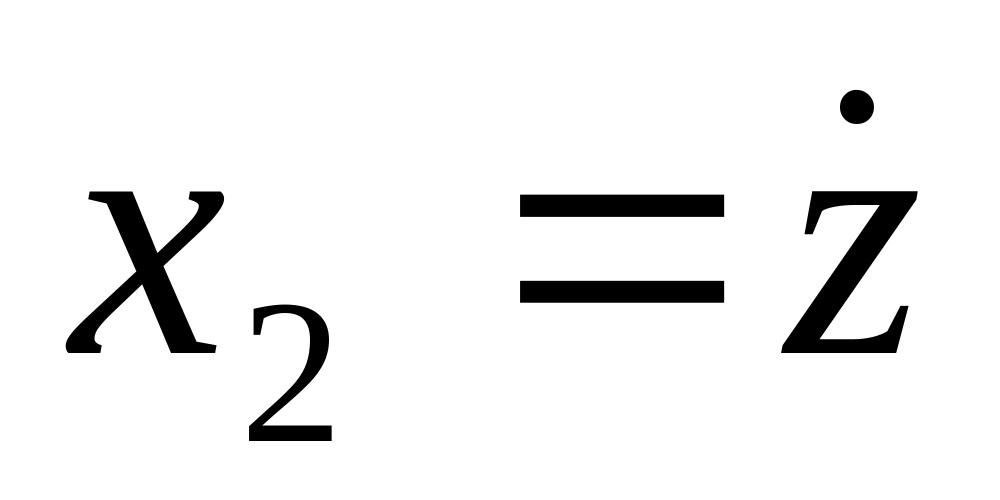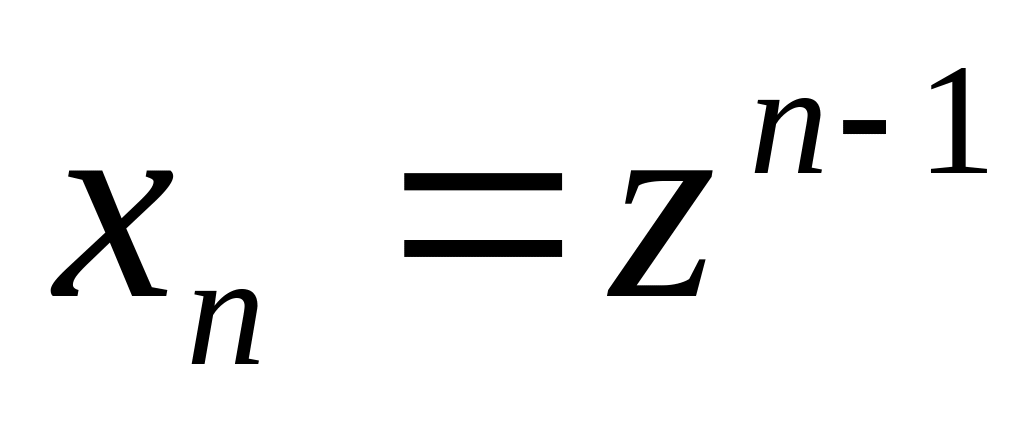(2.9)
Систему уравнений (2.9) можно представить векторно-матричной форме, соответствующей уравнениям (2.3) и (2.4), со следующими матрицами:
,
,
.
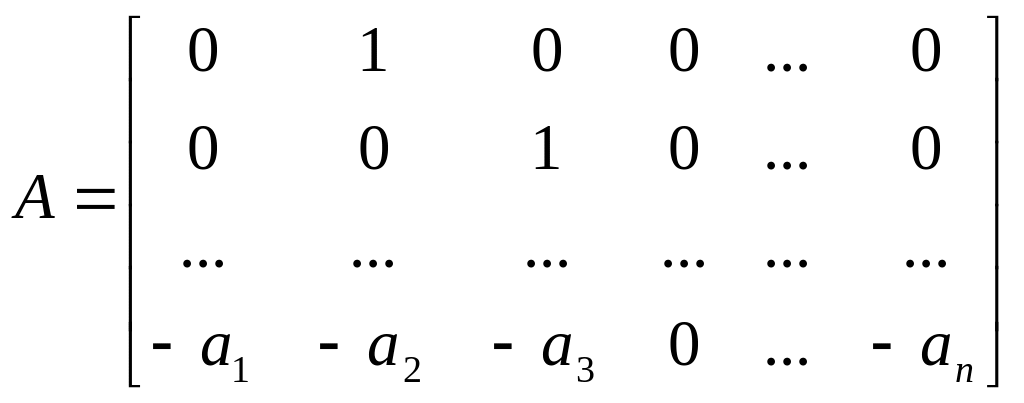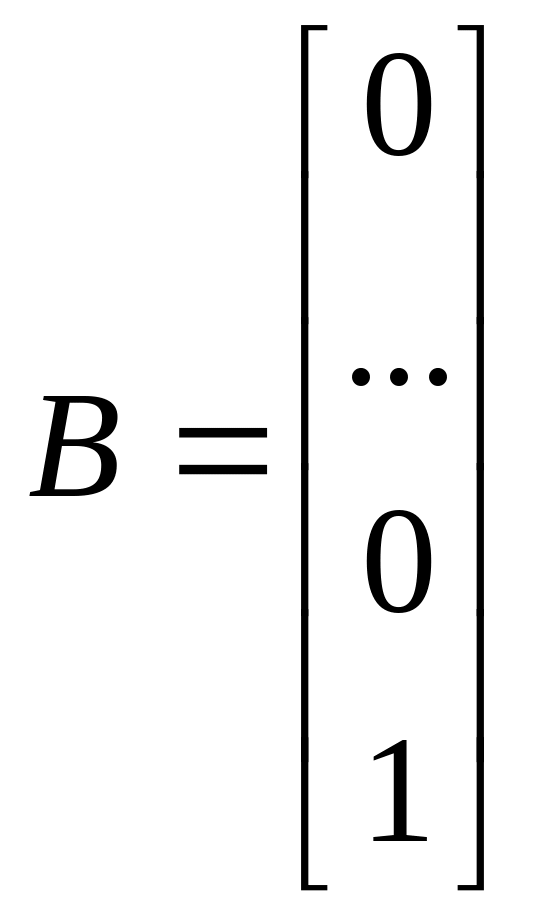Пример
Пример 2.2
Записать модель в переменных состояния, соответствующую первому каноническому описанию, определить матрицы A, B, C и изобразить структурную схему системы.
.
Решение:
Записав дифференциальное уравнение в операторной форме, получим:
.
Передаточная функция этого выражения имеет вид:
Представив передаточную функцию, как два последовательных звена, получим:
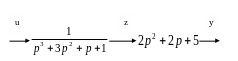
Запишем операторные уравнения через z:
Внеся z в скобки, получим:
Выразим старшую производную по
:
Нарисуем структурную схему из трех интеграторов, с обратными связями по u и производными по y.
От структурной схемы перейдем к модели в переменных состояния
Матрицы объекта имеют вид:
,
B=
,
C=
.
2.2 Вторая каноническая форма
Для перехода от передаточной функции (1.1) ко второй канонической форме необходимо:
Представить структурную схему в виде двух последовательных звеньев, соответствующих уравнению (2.6) , обозначив переход через z (рисунок 2.3);
Рисунок 2.3. Структурное представление системы, соответствующее уравнению (2.6).
Для каждого звена системы записать соответствующие операторные уравнения:
(2.10)
Определить старшую производную переменной y из первого уравнения (2.10), что соответствует значению
в операторной форме
(2.11)
Представить (2.11) в виде цепочки из n интеграторов (рисунок 2.4), где n – порядок системы. В обратной связи будут располагаться коэффициенты характеристического полинома, а в прямой связи – коэффициенты первого полинома числителя передаточной функции из формулы 2.10;
Рисунок 2.4. Структурная схема, соответствующая второй канонической форме
От полученной структурной схемы, обозначив выход каждого интегратора за переменную состояния, записать дифференциальные уравнения состояния и уравнение выхода:
(2.12)
По уравнениям (2.12) можно получить матрицы системы:
,
,
.
Пример
Пример 2.3
Записать модель в переменных состояния, соответствующую второму каноническому описанию, определить матрицы A, B, C и изобразить структурную схему системы:
.
Решение:
Записав дифференциальное уравнение в операторной форме, получим:
.
Передаточная функция этого выражения имеет вид:
Представив передаточную функцию, как два последовательных звена, получим:
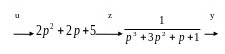
Запишем операторные уравнения через z:
Выразим старшую производную по y:
.
Нарисуем структурную схему из трех интеграторов, с обратными связями по u и производными по y:
От структурной схемы перейдем к модели в переменных состояния:
Матрицы объекта имеют вид:
,
B=
,
C=
;