Билет 14

Вопрос 1

Метод малого параметра.

(Метод Пуанкаре)

1.Предварительные рассуждения.

Метод последовательных приближений (метод Пикара), являясь довольно общим и универсальным методом, весьма плохо подходит для решения дифференциальных уравнений движения в небесной механике. Уже второе приближение этого метода дает громоздкие, неберущиеся интегралы, которые не дают никаких преимуществ перед классическим решением задачи. Кроме того, метод Пикара, в силу своей универсальности никак не учитывает математические и физические особенности уравнений движения.

Эти особенности блестяще учел и на этой основе создал свой метод, выдающийся французский ученый Жуль Анри Пуанкаре – философ, математик, небесный механик. Метод Пуанкаре или метод малого параметра получил широкое распространение в небесной механике, да и в математике в целом. Суть его заключается в следующем:

В небесной механике и космической геодезии мы имеем дело с системой дифференциальных уравнений вида:

(1)

где (2)

В случае, когда возмущения полагают равными нулю, т.е. R=0, то мы имеем дело с невозмущенным движением. Возмущенное движение чаще всего описывают системой из шести уравнений первого порядка, выраженной через элементы орбиты, т.е.

(3)

где L – матрица, не зависящая от текущих элементов.

Возмущающая функция в уравнениях (1) и (3) может быть представлена в виде

(4)

где суть константы имеющие порядок , а остальные и менее, то есть являются малыми параметрами.

Отметим, что и в теории движения планет, где тела рассматриваются в виде точечных масс, в правые части дифференциальных уравнений движения входят малые параметры в виде отношений масс планет к массе Солнца, т.е. . Но для самой большой планеты – Юпитера это соотношение равно, как известно 1: 1047, т.е. . Для остальных планет – гигантов это соотношение на порядок меньше, а для планет земной группы это соотношение составляет .

Обозначив эти параметры через , мы уравнения (1) можем записать в следующем виде:

(5)

Или в более общем виде, систему (5) можно переписать и таким образом:

(6)

Где мы выделили только один параметр (например , а остальные мы тоже можем обозначить через G).

2.Метод малого параметра для дифференциальных уравнений первого порядка с одним малым параметром.

Пусть нам дано дифференциальное уравнение первого порядка с одним малым параметром G, то есть:

при (7)

Отметим, что мы полагаем левую и правую часть (т.е. и ) n – мерными векторами, поэтому это уравнение эквивалентно одному дифференциальному уравнению n – го порядка. То есть уравнение (7) обладает довольно значимой общностью.

Определение (теорема Пуанкаре) Пусть правые части дифференциальных уравнений (7) удовлетворяют всем условиям

теоремы существования и единственности решения и, кроме того, правые части уравнения (7) разложимы в сходящийся ряд по степеням G, то есть

(8)

тогда решение данного уравнения (7) может быть найдено в следующем виде

(9)

где (9) – сходящийся к решения ряд, а - суть функции только начальных условий и времени , подлежащие определению.

Определение функций

Запишем первое приближение

(10)

т.е. первое приближение будет в точности совпадать с первым приближением по Пикару.

Найдем второе приближение

Так как мы ищем второе приближение пропорционально , то члены при и так далее приравняем к нулю и введем обозначение

Окончательно для второго приближения имеем:

(11)

Как мы видим, второе приближение по Пикару и второе приближение метода Пуанкаре совершенно разные ( и ). А именно по Пикару должно содержать все, в том числе и отброшенные нами члены. В тоже время второе приближение в методе малого параметра (Пуанкаре) не содержит предыдущих приближений в виде слагаемых, как метод Пикара, а оно входит как произведение производной от правой части по искомой переменной на первое приближение.

Третье приближение имеет вид:

Разложим подынтегральное выражение в ряд Тейлора в окрестности точки

Оставим члены пропорциональные до включительно, а степени выше третьей (т.е. ) отбросим:

Введем следующее обозначение

(12)

С учетом выражения (12) окончательно для третьего приближения можем записать

(13)

Выражение (13) с точностью до отброшенных членов дает нам третье приближение в методе Пикара, а точнее выражение третьего приближения для метода малого параметра.

С учетом вышеизложенной методики можно получить четвертое, пятое и т.д. приближения в методе Пуанкаре (малого параметра).

Метод малого параметра для дифференциальных уравнений первого порядка с двумя малыми параметрами.

Пусть нам задано стандартное дифференциальное уравнение первого порядка

(14)

при начальных условиях , которое имеет два малых параметра и

Мы полагаем, что правые части дифференциального уравнения (14) удовлетворяют теореме о существовании и единственности решения и теореме Пуанкаре, то есть правая часть разложима в сходящийся ряд вида:

(15)

В этом случае, согласно вышеупомянутой теореме, решение можно представить в виде:

(16)

Несколько слов по поводу функций и их индексации. Заметим, что индексация должна отражать:

1. от какой функци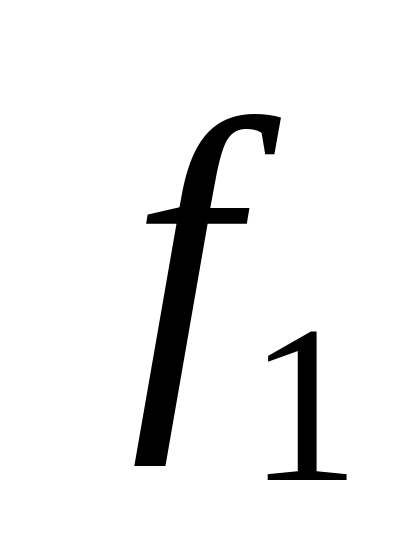и или зависят приближения.

2. какой параметр, и в какой степени перед

3. какой порядок приближения отражает та или иная функция

Мы введем минимум индексов (два) внизу которые, тем не менее, дают полную информацию на поставленные вопросы. В самом деле, говорит нам, что в m – ой степени (на что указывает первый индекс внизу), а в n – ой степени. Само выражение зависит от функции и . Если индекс n=0, то зависит только от функции , если m=0, то наоборот - зависит только от . Сумма индексов m+n говорит нам о порядке приближения.

Отыскание функции

Для этой цели, как и в случае с одним малым параметром, воспользуемся методом Пикара.

В самом деле, в методе Пикара имеем первое приближение:

(17)

Введем обозначения

(18)

Тогда выражение (17) приобретет искомый нами вид:

(19)

Как видно первое приближение метода Пикара и Пуанкаре совпадают.

Второе приближение по Пикару имеет вид:

(20)

Аналогично, как мы поступали с одним малым параметром заменим в (20) на основании (19) и разложим в ряд Тейлора в окрестности точки .

Имеем:

(21)

Но первые три члена в выражении (21) с учетом введенных обозначений (17) полностью совпадают с первым приближением (19). Что касается четырех членов в последних двух интегралах, то мы их сгруппируем по малым параметрам и . То есть имеем:

Введем новые обозначения

(22)

С учетом введенных обозначений (22) и раннее введенных (18), имеем:

(23)

Таким образом, мы получим выражения в заявленном нами виде – в виде разложений в ряды по степеням малых параметров и . Фактически у нас появляется и третий параметр порядок которого естественно равен ~ или ~ . Второй порядок в методе Пуанкаре значительно отличается от метода Пикара (выражение (20)). Сравнивая (20) и (23) мы видим, что в методе Пуанкаре мы учли то обстоятельство, что второе приближение по точности, как это видно из (20) пропорционально . Этой особенностью мы и воспользовались, отбросив во втором приближении члены пропорциональные и более высокие степени.

Имея это в виду, можно записать и третье приближение по Пуанкаре:

(24)

Найти третье приближение можно аналогично второму, разложив в ряд Тейлора третье приближение по Пикару и отбросив члены пропорциональные и их комбинации.

Функции третьего приближения по Пуанкаре будут содержать уже и вторые производные от и при коэффициентах пропорциональных и .

Метод малого параметра (Пуанкаре) при интегрировании уравнений движения.

Уравнения движения в векторной форме имеют вид:

(25)

при начальных условиях .

Как было показано во введении к методу Пуанкаре, что уравнения (25) легко представить в виде уравнений с малым параметром , то есть

при начальных условиях (26)

В координатной форме это уравнение (6).

Поставим задачу: получить решение системы(26) в следующем виде

(27)

где - векторы невозмущенных координат и скоростей, а и - возмущения, вызванные пертурбационной функцией R в выражении (26). При этом возмущения в координатах и скоростях будем искать методом малого параметра, то есть в следующем виде:

(28)

Решение поставленной задачи

Задачу разобьем на два этапа

Первый этап. На первом этапе будем полагать и , то есть, полагаем, что уравнения движения являются невозмущенными уравнениями. Но решение уравнений невозмущенного движения известно. То есть для

(29)

Мы имеем решение

(30)

Напомним, их в координатной форме

(31)

Аналогичные выражения имеются и для скоростей, то есть для . Кстати, их легко получить из (31) если продифференцировать это выражение по .

Второй этап. Вернемся к исходной системе дифференциальных уравнений (26). Решение этой системы методом малого параметра (Пуанкаре) состоит в доказанной возможности представлять сами исходные уравнения в виде степенных рядов по малому параметру , то есть

(32)

Кстати выражение (32) легко получить из выражений (27), так как согласно методу Пуанкаре и суть степенные ряды по малому параметру . Дифференцируя их два раза для координат, и один раз для скоростей, мы прейдем к выражению (32). Будем полагать, и это доказано Пуанкаре, что такое разложение (32) существует, но существует и решения в виде (27). Тогда (32) можно переписать:

Разложим правые части в ряд Тейлора и ограничимся вторым порядком точности, то есть будем отбрасывать все члены пропорциональные и выше. Учитывая (28) имеем:

Все члены при производных второго порядка и выше отбрасываем. Приравниваем при равных степенях слева и справа. Для получим:

(33)

Распишем уравнение (33) в координатной форме, полагая и с компонентами согласно выражению (6):

(34)

Подобным образом приравниваем члены пропорциональные :

(35)

Уравнение (34) в координатной форме имеет вид

+

;

; (36)

;

Введем некоторые обозначения, которые позволят нам записать выражение (34) и (36) в векторно-матричном виде и унифицировать записи для уравнений пропорциональных и так далее. В самом деле, обозначим

(37)

Тогда для второго приближения введем функции и , но, как мы видим из выражения (36) это довольно сложные выражения. В операторно-матричной форме будет иметь вид

(38)

Третье приближение запишется аналогично:

(39)

Кроме того, введем обозначения

(40)

и обозначим через Р матрицу этих производных:

(41)

В принятых обозначениях уравнения для первого, второго, третьего и последующих приближений можно записать одним векторным уравнением:

(42)

где , а Р согласно обозначению (41).

Первое приближение. Полагают в первом приближении, что , тогда мы имеем невозмущенную систему

(43)

у которой матрица Р является матрицей констант, то есть Р не зависит от , а зависит только от начальных условий. Поэтому из (43) мы сразу же получим:

(44)

Пусть мы нашли шесть интегралов, при этом получили шесть произвольных постоянных интегрирования и . То есть мы имеем:

Общее решение представляет собой линейную комбинацию частных решений

(45)

где ,

В нашем конкретном случае это

(46)

где - это шестимерный вектор элементов орбиты.

Из теории линейных дифференциальных уравнений известно, что не только сами решения (44) будут удовлетворять исходной системе (43), но и их частные производные и по произвольным постоянным, в данном случае по элементам орбиты. То есть решение системы (43) будут:

(47)

В этом случае система (43) приобретет вид:

(48)

Общее решение (с учетом приближений) можно записать в виде:

(49)

Для мы записывать не будем, так как его легко можно получить простым дифференцированием по , учитывая, что от времени не зависит. Но полученное решение прекрасно удовлетворяет системе (43) (линейные однородные уравнения), но удовлетворять исходной системе (42) естественно не будет, так как эта система совсем другая – она даже не является линейно однородной.

Второе и последующие приближения. Ставится задача найти общее решение (47) или (49) линейной однородной системы (43) таким образом, чтобы решение

а) имело тот же аналитический вид

б) сохраняло алгоритмы решения

То есть вид формул и их применение должны быть инвариантны как по отношению к системе (43), так и к системе (42).

Как это можно сделать? Еще до Пуанкаре Лагранж блестяще решил поставленную задачу – применив метод вариации произвольной постоянной. То есть в этом случае Пуанкаре в соответствии с методом Лагранжа положил, что для возмущенной системы решение должно быть найдено под условием, что вектор констант является функцией времени и эти функции необходимо искать под следующими условиями

Во – первых, чтобы эти функции в определенных комбинациях составили решение системы (42)

Во – вторых, чтобы вид этих формул, составляющих решение был таким же, как и для невозмущенной системы (41) и как следствие второго

В третьих, алгоритмы решения при переходе от невозмущенной системы (43) к возмущенной (42) не должен меняться.

Таким образом, Пуанкаре в методе малого параметра, используя метод Лагранжа, варьирует константами невозмущенного движения (элементами орбиты) системы (43) таким образом, чтобы

а) сохранить вид формул решений в невозмущенной и возмущенной системах (42) и (43), и

б) сохранить алгоритмы решения для линейной (43) и нелинейной (42) систем

Итак, мы имеем решение системы (43) в виде (49). Продифференцируем (49) по :

(50)

Заметим, что (50) дает нам и дополнение к решению (43) для скоростей, но в невозмущенной системе , поэтому . Но ведь мы желаем, чтобы решение для возмущенной системы было по форме таким же, как и в невозмущенной системе. То есть в (50) нам необходимо положить , но не за счет того, что как в невозмущенной системе , напротив , но

(51)

Продифференцируем упростившееся выражение (50) за счет условия (51). Имеем:

(52)

Подставим полученные выражения (49) и (52) в исходную систему (42). Имеем:

(53)

Согласно доказанной Пуанкаре теореме, с целью выполнения поставленных нами раннее условий, необходима расщепить систему (53) на две системы

1. (54)

2. (55)

Далее решают систему (54) чисто алгебраически, объединив ее с системой (49), то есть имеем:

(56)

Введем обозначения

(57)

(58)

(59)

Имеем с учетом обозначений (57) – (59) для системы (56):

(60)

Откуда

(61)

(62)

Если нам заданы начальные условия , то поставив условие, чтобы мы найдем , тогда (62) примет вид:

(63)

Можно поступить и по другому. Предположить, что - вектор констант невозмущенного движения, тогда . Пуанкаре в своей известной теореме доказал, что при найденных значениях уравнение (55) тождественно обращается в 0.

Поэтому уравнение (49) дают нам решение абсолютно совпадающем по виду с решением невозмущенной системы с той разницей, что в возмущенной системе элементы орбиты зависят от времени, а в невозмущенной – они константы.

Имеем:

(64)

Для скоростей на основании (50) с учетом (51) имеем:

(65)

Понятно, что координаты и скорости удобно находить в едином блоке

(66)

Общее решение примет вид:

(67)