17. Передаточные функции механизма

В машинах приходится движением одной из ее частей А вызывать движение другой части В и притом так, что первая часть или надавливанием, или трением приводит в движение другую часть, которая таким же образом двигает третью и т. д., пока движение не сообщится части В. Совокупность всех частей, передающих движение от части А к части В, и называется П. механизмом. Например, в карманных часах система колес, передающая движение заводной пружины стрелкам, представляет собой П. механизм, или просто — передачу. Если вращательное движение одного шкива передается другому с помощью ремня, цепи или проволочного каната, то такого рода передачи называют соответственно: ременной, цепочной или канатной. Зубчатой передачей называется система зубчатых колес.

18. Планы скоростей плоских рычажных механизмов

Построение планов скоростей и ускорений ведется в порядке присоединения групп Ассура к начальному механизму. Поскольку кривошипно-ползунный механизм имеет одну степень подвижности, то заданное движение входного звена (в данном случае кривошипа О₁А) определяет движение всех остальных звеньев. Т.к. звено О₁А совершает вращательное движение, то траекторией точки А является окружность с центром в точке О₁. Вектор скорости точки А направлен по касательной к траектории движения, т.е. перпендикулярно радиусу О₁А, в сторону вращения кривошипа. Величина скорости определяется из выражения:

,

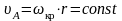где _{кр .}- угловая скорость кривошипа, рад/с; r – радиус кривошипа, м.

Известный по величине и направлению вектор скорости _А строят в виде отрезка произвольной длины р_а, из выбранного полюса р_ - плана скоростей (рис. 3.9, б). В этом случае масштаб плана скоростей:

, .

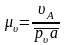При определении скорости точки В следует отметить, что ползун совершает возвратно-поступательное движение, т.е. траекторией его движения является прямая линия, а вектор её скорости направлен параллельно линии перемещения. Т.к. точка В одновременно принадлежит и ползуну, и шатуну, то для дальнейшего построения плана скоростей следует воспользоваться векторным уравнением, выражающим связь между скоростями точек А и В шатуна:

,

где – вектор абсолютной скорости точки В; – вектор скорости переносного движения, скорости полюса в качестве которого принята точка А; – вектор относительной скорости точки В по отношению к точке А (вектор вращательной скорости точки В вокруг полюса – точки А).

В векторном равенстве две неизвестные величины: скорость _В и относительная (вращательная) скорость _ВА. Вектор абсолютной скорости направлен параллельно линии перемещения ползуна ХХ, а вектор относительной скорости – перпендикулярно радиусу вращения, т.е. перпендикулярно текущему положению шатуна АВ. Вектор переносной скорости (скорости полюса) на плане скоростей представлен отрезком р_а, поэтому данное векторное равенство можно решить графическим путем.

Через точку а вектора р_а проводят линию действия скорости _ВА перпендикулярно АВ. Далее, в соответствии с векторным уравнением, через полюс плана скоростей р_ проводят линию действия скорости _В параллельно линии ХХ перемещения ползуна. На пересечении линий действия скоростей _ВА и _В находим точку в, расстояние от которой до полюса плана в масштабе и определяет величины скоростей, м/с:

; .

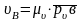Зная относительную скорость точки В вокруг полюса точки А, можно определить угловую скорость шатуна, рад/с:

,

где _ВА - м/с; l – длина шатуна, м.

Теорема подобия фигур для планов скоростей: фигуры на плане положений и на плане скоростей образованные векторами относительных скоростей подобны. Рассмотрим треугольники на плане положений 0₁АВ и на плане скоростей р_ав, они являются подобными как имеющими две стороны взаимно перпендикулярные друг другу и одну параллельную.

Для определения скоростей центров тяжести звеньев следует найти положения точек S₁ и S₂ на плане скоростей, воспользовавшись теоремой подобия составив соотношения:

и ,

т.е. абсолютная скорость .

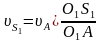Чтобы получить абсолютную скорость точки S₂ следует соединить точку s₂ с полюсом плана скоростей р_ , и тогда отрезок р_s₂ определит в масштабе плана _ скоростей абсолютную скорость центра тяжести шатуна. Истинное значение абсолютной скорости точки S₂ определяем, м/с:

.