25. Приведение сил и масс. Графический способ

13. Приведение сил. Графический способ.

О движении всех звеньев машины можно судить по движению одного звена, так как движение всех звеньев взаимосвязаны. Звено, по движению которого судят о характере работы машины, называется главным.

За главное звено обычно принимают ведущее звено, так как оно непосредственно связано с двигателем. Чтобы иметь право судить по движению главного звена о движении остальных звеньев, необходимо учесть силы и моменты, действующие на все звенья механизма, а также массы и моменты инерции всех звеньев. Для этого все силы и массы приводят к главному звену.

Приведенной силой (моментом) называется такая сила (момент) приложения к главному звену, которая развивает мощность равную сумме мощностей приводимых сил и моментов:

Если главное звено совершает поступательное движение, то удобно все силы и заменять эквивалентной по своему действию на механизм приведенной силой. Если главное звено вращается (что встречается гораздо чаще), то определяют приведенный момент.

14. Приведение масс. Графический способ.

П риведенной массой (моментом инерции) называется такая условная масса (момент инерции), обладая которой главное звено имеет кинетическую энергию, равную сумме кинетических энергий приводимых масс и моментов инерции:

Здесь также удобно определять приведенную массу, если главное звено движется поступательно, и определять приведенный момент инерции, если главное звено совершает вращательное движение.

После приведения сил и масс к главному звену определяется его истинный закон движения.

26. Уравнение движения механизма

Выполнив приведение сил и масс, любой механизм с одной степенью свободы (рычажный, зубчатый, кулачковый и др.), сколь бы сложным он ни был, можно заменить его динамической моделью (рис. 5.2). Эта модель в общем случае имеет переменный приведенный момент инер- ции   и к ней приложен суммарный приведенный момент  . Закон движения модели такой же, как и закон движения начального звена механизма (см. 5.1).

Рис. 5.2. Динамическая модель механизма с W = 1

 после приведения сил и масс

Основой для составления уравнения движения механизма с одной степенью свободы служит теорема об изменении кинетической энергии:

Т – Т_нач  = А_Σ .(5.2)

Работу совершают все активные силы и моменты и силы трения во всех кинематических парах механизма.Уравнение движения в энергетической форме. Запишем формулу для кинетической энергии модели, учитывая уравнение (5.1):

(5.3)

Так как вся нагрузка, приложенная к модели, выражается суммарным приведенным моментом  , то сумма работ равна

  _(5.4)

Здесь переменная интегрирования φ_м заменена координатой φ₁ начального звена, так как φ_м = φ₁.

Подставив выражения (5.4) в (5.2), получим уравнения движения в энергетической форме:

 _(5.5)

где искомой величиной является угловая скорость φ₁ начального звена механизма.

В общем случае верхний предел φ₁ интегрирования в равнении (5.5) считается переменным. Если вся нагрузка, приложенная к механизму, зависит только от его положения, то и суммарный приведенный момент  есть функция только координаты φ₁. В этом случае уравнение (5.5) решается непосредственно относительно искомой величины ω₁:

(5.6)

Укажем, что интеграл под корнем имеет знак, который необходимо учитывать.Уравнение движения в дифференциальной форме.Продифференцируем (5.5) по координате φ₁:

Определим производную, стоящую в левой части уравнения, помня, что в общем случае переменной величиной является не только угловая скорость ω₁, но и   . Поэтому

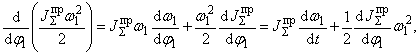
откуда

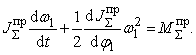(5.7)

Это и есть уравнение движения в дифференциальной форме, поскольку искомая переменная величина – угловая скоростьω₁ начального звена механизма – стоит под знаком производной. При пользовании уравнением (5.7) следует помнить, что суммарный приведенный момент  , а также производная d /dφ₁ величины алгебраические и подставляются со своими знаками.

В том случае, когда исследуется механизм, имеющий   = const (например, зубчатый механизм с круглыми центроидами), уравнение его движения упрощается и приобретает вид

 (5.8)

Уравнение движения в дифференциальной форме (5.7) может быть получено также и из уравнения Лагранжа второго рода.Для определения углового ускорения  ₁  начального звена используем уравнение (5.7) и решаем его относительно 

(5.9)

Величины   и d /dφ₁  подставляются в уравнение (5.9) со своими знаками. Если угловое ускорение  ₁ получится со знаком, противоположным знаку угловой скорости ω₁, значит, начальное звено механизма движется замедленно.Производную d /dφ₁  подсчитывают численным дифференцированием или графическим дифференцированием. Необходимо отметить, что существует другой значительно более точный (но и более трудоемкий) способ определения производной d /dφ₁ , который можно найти в специальной литературе.