22. Классификация случайных величин.

По типу структуры множества их возможных значений случайные величины делятся на дискретные и непрерывные.

Дискретной случайной величиной называют случайную величину, число возможных значений которой конечное либо счётное множество.

Примеры:

• X - частота попаданий при трёх выстрелах. Возможные значения: =0, =1/3, =2/3, =1

• X- число дефектных изделий из n штук. Возможные значения: =0, =1, =2… …

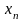• X – число выстрелов до первого попадания. Возможные значения: =1, =2, =3… =n

Непрерывной случайной величиной называют такую случайную величину, возможные значения которой непрерывно заполняют некоторый промежуток (конечный или бесконечный).

Примеры:

• X - случайное отклонение по дальности от точки попадания до цели при выстреле из орудия. Так как снаряд может попасть в любую точку, интервала, ограниченного минимальным и максимальным значениями дальности полёта снаряда, возможных для данного орудия, то возможные значения случайной величины X заполняют промежуток между минимальным и максимальным значением.

• X - ошибки при измерении радиолокатором.

• X - время работы прибора.

23. Способы задания свдт.

Дискретной называют случайную величину, возможные значения (конечные или бесконечные) которой есть отдельные изолированные числа (т.е. между двумя соседними возможными значениями нет возможных значений и их можно пронумеровать), которые эта величина принимает с определенными вероятностями.

Л юбой способ задания случайной величины называется законом распределения этой величины. Законом распределения СВДТ является перечень ее возможных значений и соответствующих им вероятностей. Записывается в виде таблицы:

– сумма ряда вероятностей должна быть равна единице.

Или может быть записан аналитически – Р (Х=х_i) = φ(х_i)

Также закон распределения СВДТ можно изобразить графически в виде многоугольника распределения. Для этого в системе координат строят точки М₁(х₁;p₁), М₂(х₂;p₂)… М_n(х_n;p_n).

1. Равномерное распределение СВДТ Х, принимающей n значений, задается формулой: P_n(x=x_i)=1/n

2 . Биномиальный закон распределения СВДТ Х – проводятся n-однотипных независимых испытаний, в каждом из которых может произойти или не произойти С ОДНОЙ И ТОЙ ЖЕ ВЕРОЯТНОСТЬЮ событие А, интересующее нас. Его вычисляют по формуле Бернулли:

Е сли число испытаний (n) велико, а вероятность p появления события в каждом испытании очень мала, то используют распределение СВДТ по закону Пуассона: , где k – число появлений события в n независимых испытаниях, λ = np (среднее число появлений события в n испытаниях).

3. Геометрическое распределение СВДТ Х – опыт состоит в проведении однотипных независимых испытаний, в каждом из которых может произойти ожидаемое нами событие А, при этом испытания проводят до первого появления события А (!): Р_n (x=k) = pq^k-1

4 . Гипергеометрическое распределение СВДТ Х – осуществляется безвозвратная выборка m – элементов из имеющихся n – элементов, причем эти n – элементы двух типов: n₁ элемент обладает нужными нам значениями признака, n₂ – нет, а в сумме n₁ + n₂ = n. Формула: