
Билет №1.
1)Функции y=cosx, её свойство и график.
2)Найдите наибольшее и наименьшее значение.
1) Свойства функции y=cosx
1. Область определения - множество R всех действительных чисел
2. Множество значений - отрезок [−1;1]
3. Функция y=cosx периодическая с периодом 2π
4. Функция y=cosx - чётная
5. Функция y=cosx принимает:
- значение, равное 0, при x=π2+πn,n∈Z;
- наибольшее значение, равное 1, при x=2πn,n∈Z
- наименьшее значение, равное −1, при x=π+2πn,n∈Z
- положительные значения на интервале (−π2;π2) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z
- отрицательные значения на интервале (π2;3π2) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z
6. Функция y=cosx
- возрастает на отрезке [π;2π] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z
- убывает на отрезке [0;π] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z

2)
Билет №2.
1)Функция y=sinx,её свойство и график.
2)Решите неравенство.
1) Свойства функции y=sinx
1. Область определения - множество R всех действительных чисел.
2. Множество значений - отрезок [−1;1]
3. Функция y=sinx периодическая с периодом T=2π
4. Функция y=sinx нечётная.
5. Функция y=sinx принимает:
- значение, равное 0, при x=πn,n∈Z
- наибольшее значение, равное 1, при x=π2+2πn,n∈Z
- наименьшее значение, равное −1, при x=−π2+2πn,n∈Z
- положительные значения на интервале (0;π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z
- отрицательные значения на интервале (π;2π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z
6. Функция y=sinx
- возрастает на отрезке
[−π2;π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z
- убывает на отрезке
[π2;3π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z

2)Sin t > ½.
Решение. Учтём, что sin t – это ордината точки M(t) числовой окружности. Значит, нам нужно найти на числовой окружности точки с ординатой y > ½ и записать, каким числам t они соответствуют.
Ответ: π/6 + 2πK< t < 5π/6 + 2πK
Билет №3 .
Функция y=tgx, её свойство и график.
Решить неравенство .
1) Свойства функции y=tgx
1. Область определения - множество всех действительных чисел x≠π2+πn,n∈Z
2. Множество значений - множество R всех действительных чисел
3. Функция y=tgx периодическая с периодом π
4. Функция y=tgx нечётная
5. Функция y=tgx принимает:
- значение 0, при x=πn,n∈Z;
- положительные значения на интервалах (πn;π2+πn),n∈Z;
- отрицательные значения на интервалах (−π2+πn;πn),n∈Z.
6. Функция y=tgx возрастает на интервалах (−π2+πn;π2+πn),n∈Z.
2)
 Решить неравенство: а)tg
t >
Решить неравенство: а)tg
t > .
.
Решение. А)
Отметим на линии тангенсов точку P=P(
).
Неравенство tg t
>
означает, что нас интересуют на этой
прямой точки, лежащие выше точки Р.
Прямая ОР пересекает числовую окружность
в точках М1, М2;
точкам, расположенным выше точки Р,
соответствуют точки открытых дуг М1В,
М2D. Аналитическая запись
дуги М1В такова; 4 /3
+ 2
K<
t < 3
/2
+ 2
K.
Эти две серии решений можно объединить
/3
+ 2
K<
t < 3
/2
+ 2
K.
Эти две серии решений можно объединить
 +
+
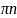 < t <
< t <
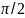 +
.
+
.
Билет №4.
Решите простейшее уравнение sinx=а.
Найдите производную функции.
1)Пример:
Найти arcsin12
Выражениеarcsin12 показывает, что синус угла x равен12 , т.е. sinx=12.
Далее просто находим точку этого синуса на числовой окружности, что и является ответом:

точка12, находящаяся на оси y, соответствует точке π6 на числовой окружности. Значит,arcsin12=π6
Обрати внимание!
Если sinπ6=12, то arcsin12=π6
В первом случае по точке на числовой окружности находим значение синуса, а во втором – наоборот, по значению синуса находим точку на числовой окружности. Движение в обратную сторону. Это и есть арксинус.
Теорема. Для любого a∈[−1;1] справедлива формула arcsin(−a)=−arcsina
Частные случаи: 1. sinx=0⇒x=πk,k∈Z.
2. sinx=1⇒x=π2+2πk,k∈Z
3.sinx=−1⇒x=−π2+2πk,k∈Z
2)

Билет №5
Решите простейшее уравнение cosx=a.
Найдите критические точки.
1) Пример:
Найти arccos2√2
Выражение arccos2√2 показывает, что косинус угла xравен 2√2 (cosx=2√2).
Далее просто находим точку этого косинуса на числовой окружности, что и является ответом:

число , являющееся значением осиx, соответствует точкеπ4 на числовой окружности.
Значит,arccos2√2=π4
Обрати внимание!
если cosπ4=2√2, тоarccos2√2=π4
В первом случае по точке на числовой окружности определяем значение косинуса, а во втором – наоборот, по значению косинуса находим точку на числовой окружности. Движение в обратную сторону. Это и есть арккосинус.
Теорема. Для любого a∈[−1;1] выполняется равенство arccosa+arccos(−a)=π
Частные случаи:
1.cosx=0⇒x=π2+πk,k∈Z
2.cosx=1⇒x=2πk,k∈Z
3.cosx=−1⇒x=π+2πk,k∈Z
Пример:
Решить уравнение cosx=25
Используем формулу x=±arccosa+2πk,k∈Z и получаем ответx=±arccos25+2πk,k∈Z
2)
Билет №6.
