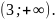Частина друга
Розв’яжіть завдання 2.1-2.6. Запишіть відповідь у бланк відповідей.
2.1.
Чому дорівнює значення виразу
.
2.2.
Знайдіть
область визначення функції
2.3.
Для функції
знайдіть первісну, графік якої проходить
через точку
2.4.
Розв’яжіть рівняння
2.5.
Площа
ромба дорівнює
,
а його діагоналі відносяться як 5 : 12.
Знайдіть периметр ромба.
2.6. В посудині, що має форму циліндра, рівень води перебуває на висоті 45 см. На якій висоті перебуватиме рівень води, якщо її перелити в посудину циліндричної форми, радіус якої втричі більший за радіус основи.
Частина третя
Розв’язання завдань 3.1-3.7 повинні мати обґрунтування. У них потрібно записати послідовні логічні дії, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1.
Розв’яжіть рівняння
.
3.2.
Побудуйте графік функції
.
3.3.
Радіуси нижньої та верхньої основ
зрізаного конуса відповідно дорівнюють
R
і r,
а його твірна нахилена до площини нижньої
основи під кутом
.
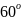Знайдіть площу бічної поверхні зрізаного
конуса.
3.4м
.
Для кожного значення параметра a
вкажіть кількість точок перетину графіка
функції
і
прямої
.
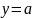3.5м
.
Розв’яжіть нерівність
3.6м . Пряма, паралельна стороні АС трикутника АВС, перетинає сторони АB та ВС в точках M і N. Ці точки з’єднані з довільною точкою К, що належить стороні АС. Знайдіть площу чотирикутника MBNK , коли відомо, що площі трикутників АВС і MNK відповідно дорівнюють Q і q.
3.7м.
У правильній трикутній піраміді плоский
кут при вершині дорівнює
Навколо цієї піраміди описано кулю,
радіус якої дорівнює R.
Знайдіть об’єм піраміди.
ВАРІАНТ 7
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповіді, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначте її у бланку відповідей.
1.1. Обчисліть
А) |
|
Б) |
|
В) |
|
Г) |
|
1.2.
Розв’яжіть систему рівнянь
А) |
|
Б) |
|
В) |
|
Г) |
|
1.3.
Спростіть
А) |
|
Б) |
|
В) |
|
Г) |
|
1.4.
(
)
– геометрична прогресія,
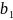= 16, q =
. Знайдіть
.
А) |
|
Б) |
|
В) |
|
Г) |
|
1.5. Яка з даних функцій є непарною ?
А) |
|
Б) |
|
В) |
|
Г) |
|
1.6.
Розв’яжіть нерівність
(x
+ 1)
(3
x).
А) |
|
Б) |
|
В) |
|
Г) |
|
1.7.
Знайдіть похідну функції
.
А) |
|
Б) |
|
В) |
|
Г) |
|
1.8.Знайдіть площу фігури, обмеженої лініями y = 2x , y = 0, x = 1, x = 3.
А) |
|
Б) |
|
В) |
|
Г) |
|
1.9.
Промінь PK
проходить між сторонами
APB,
APK
= 25
,
KPB
= 35
.
Знайдіть градусну міру
APB.
А) |
|
Б) |
|
В) |
|
Г) |
|
1.10.
Довжина кола дорівнює 6
см. Знайдіть площу круга, який обмежується
цим колом.
А) |
|
Б) |
|
В) |
|
Г) |
|
1.11. Знайдіть об’єм прямокутного паралелепіпеда, лінійні розміри якого дорівнюють 3 см, 4 см і 5 см.
А) |
|
Б) |
|
В) |
|
Г) |
|
1.12. Прямі a і b паралельні у просторі, а пряма c перетинає пряму a. Як можуть бути розташовані прямі b і c ? Виберіть правильне твердження.
А) прямі b і c можуть бути паралельними, не можуть бути мимобіжними або перетинатися;
Б) прямі b і c можуть перетинатися, не можуть бути паралельними або мимобіжними;
В) прямі b і c можуть бути мимобіжними, не можуть бути паралельними або перетинатися;
Г) прямі b і c можуть перетинатися або бути мимобіжними, не можуть бути паралельними.