Контрольная работа № 1 Вариант 9
1. Вычислить определитель
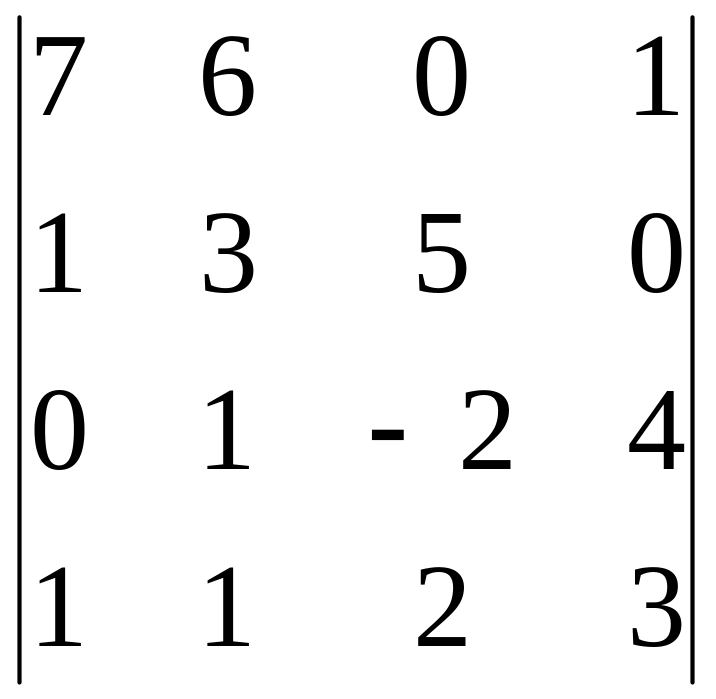
2. С матрицами А, В, С совершить указанные действия. Найти обратную к матрице А.
А=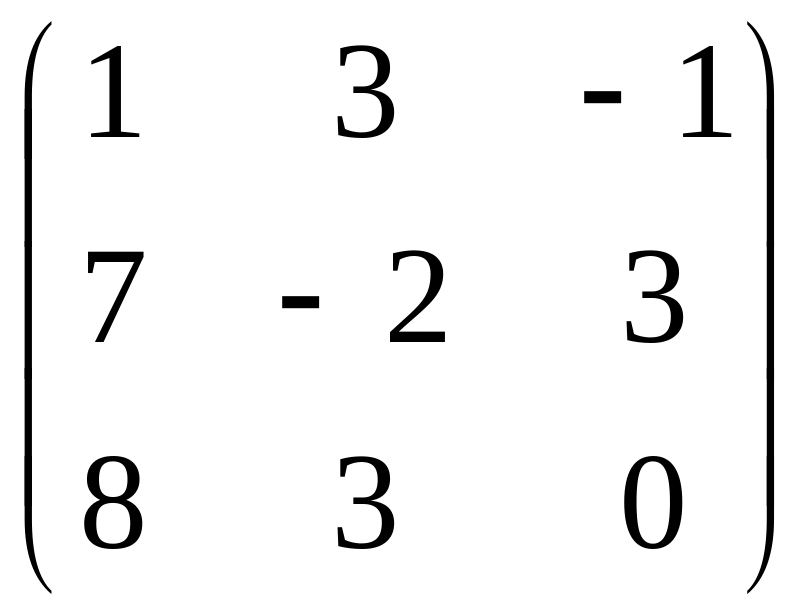
,
В=
,
С=
.
-5А+В, ВТС
3. Найти ранг матрицы.
4. Решить системы линейных уравнений: а) методом Крамера; б) методом Гаусса.
а)
б)
5. Исследовать системы на совместность. Для совместных систем найти решение.
а)
б)
6. Даны векторы а,b,с. Найти:
а) длины этих векторов;
б) скалярное произведение векторов а и b и косинус угла между ними;
в) векторное произведение а×b и площадь треугольника, построенного на этих векторах;
г) смешанное произведение аbс и объём тетраэдра, построенного на этих векторах.
a(2,5,-1), b(4,7,8), c(1,0,3)
7. Даны точки А, B, C, D. Требуется:
а) написать уравнения прямой (CD), плоскости АВС;
б) найти расстояние от точки D до плоскости АВС;
в) найти точку пересечения прямой l с плоскостью АВС;
A(2,3,2),
B(1,3,6),
C(0,4,2),
,D(2,5,4),
l:
Контрольная работа № 1 Вариант 10
1. Вычислить определитель
2. С матрицами А, В, С совершить указанные действия. Найти обратную к матрице А.
А=
,
В=
,
С=
.
3А+2В, АТСТ
3. Найти ранг матрицы.
4. Решить системы линейных уравнений: а) методом Крамера; б) методом Гаусса.
а)
б)
5. Исследовать системы на совместность. Для совместных систем найти решение.
а)
б)
6. Даны векторы а,b,с. Найти:
а) длины этих векторов;
б) скалярное произведение векторов а и b и косинус угла между ними;
в) векторное произведение а×b и площадь треугольника, построенного на этих векторах;
г) смешанное произведение аbс и объём тетраэдра, построенного на этих векторах.
a(6,-1,4), b(0,3,2), c(3,8,-2)
7. Даны точки А, B, C, D. Требуется:
а) написать уравнения прямой (CD), плоскости АВС;
б) найти расстояние от точки D до плоскости АВС;
в) найти точку пересечения прямой l с плоскостью АВС;
A(2,0,3),
B(1,-1,6),
C(0,0,2),
D(2,1,4),
l:
Контрольная работа № 1 Вариант 11
1. Вычислить определитель
2. С матрицами А, В, С совершить указанные действия. Найти обратную к матрице А.
А=
,
В=
,
С=
.
-5А+6В ВТСТ
3. Найти ранг матрицы.
4. Решить системы линейных уравнений: а) методом Крамера; б) методом Гаусса.
а)
б)
5. Исследовать системы на совместность. Для совместных систем найти решение.
а)
б)
6. Даны векторы а,b,с. Найти:
а) длины этих векторов;
б) скалярное произведение векторов а и b и косинус угла между ними;
в) векторное произведение а×b и площадь треугольника, построенного на этих векторах;
г) смешанное произведение аbс и объём тетраэдра, построенного на этих векторах.
a(2,5,-1), b(7,4,3), c(1,0,-3)
7. Даны точки А, B, C, D. Требуется:
а) написать уравнения прямой (CD), плоскости АВС;
б) найти расстояние от точки D до плоскости АВС;
в) найти точку пересечения прямой l с плоскостью АВС;
A(4,5,1),
B(
3,0,2), C(
1,2,-1), D(4,-4,1)
l:
Контрольная работа № 1 Вариант 12
1. Вычислить определитель
2. С матрицами А, В, С совершить указанные действия. Найти обратную к матрице А.
А=
,
В=
,
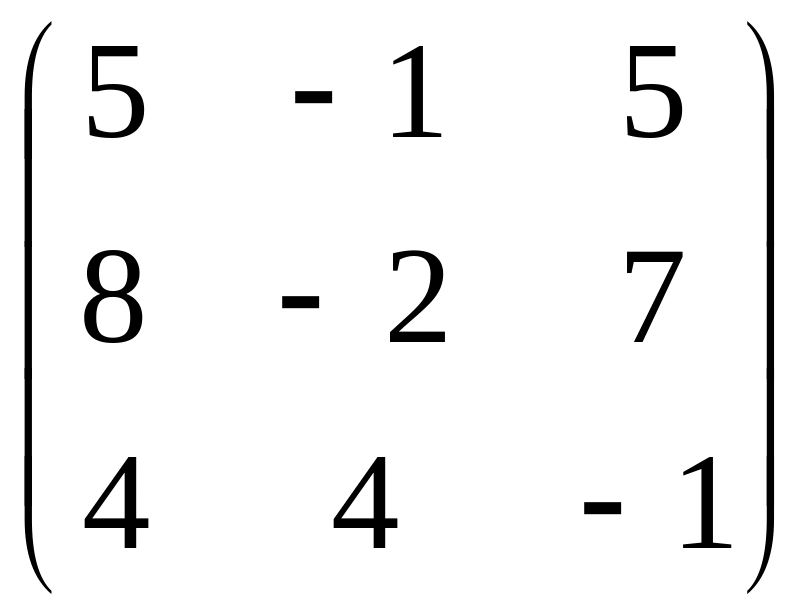С=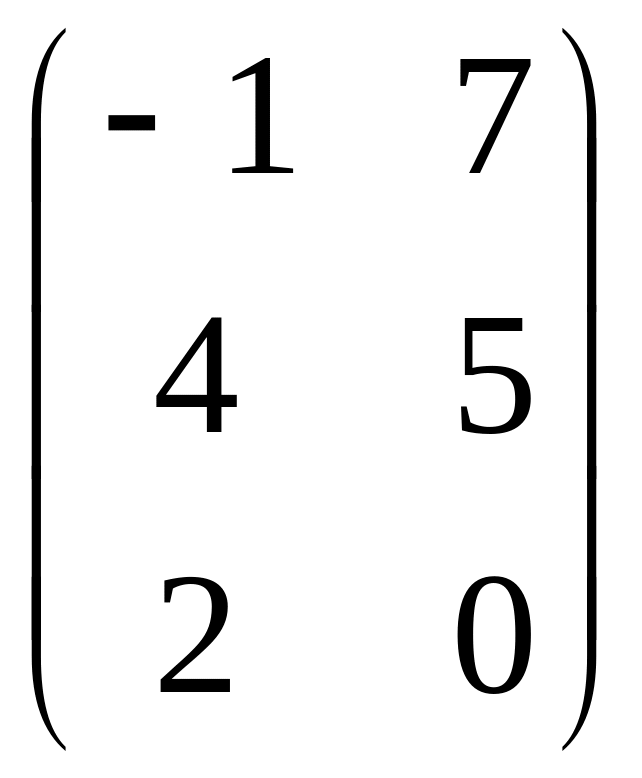
.
5А-4В, СТВ
3. Найти ранг матрицы.
4. Решить системы линейных уравнений: а) методом Крамера; б) методом Гаусса.
а)
б)
5. Исследовать системы на совместность. Для совместных систем найти решение.
а)
б)
6. Даны векторы а,b,с. Найти:
а) длины этих векторов;
б) скалярное произведение векторов а и b и косинус угла между ними;
в) векторное произведение а×b и площадь треугольника, построенного на этих векторах;
г) смешанное произведение аbс и объём тетраэдра, построенного на этих векторах.
a(-4,2,8), b(1,2,3), c(5,0,1)
7. Даны точки А, B, C, D. Требуется:
а) написать уравнения прямой (CD), плоскости АВС;
б) найти расстояние от точки D до плоскости АВС;
в) найти точку пересечения прямой l с плоскостью АВС;
A(-1,2,1),
B(0,-1,6),
C(-1,0,2,),
D(1,1,4),
l:
