2.3.7. Математическая модель для замирания канала

Замирание канала часто моделируется как канал с замираниями Накагами. Функция плотности вероятности (PDF) мгновенного SNR канала γ с замиранием Накагами задается так:

, (2.4)

В (2.4) n управляет серьезностью замирания, Γ (n) - гамма-функция, которая определяется так:

Где - среднее ОСШ канала. Если n = 1, PDF в (4) сводится к PDF γ над замиранием Рэлея и задается следующим образом:

Если значение n растет, канал ведет себя как при райсовском замирании, а при n, стремящемся к ∞, - сводится к каналу AWGN.

Пусть Рк - вероятность выбора к-режима из K схем возможных модуляций. Пусть ξ - качество метрики канала. Таким образом, Pk может быть вычислена как функция ξ:

(2.5)

В (2.5) означает переключение режимов уровней, а является PDF ξ. Среднюю пропускную способность В (среднее число битов в секунду) можно вычислить:

Где является пропускной способностью отдельных мод. Когда = ∞, средняя пропускная способность В может быть вычислена так:

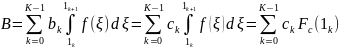
Где является комплементарной интегральной функцией распределения (CDF) и определяется:

Если мгновенное значение ОСШ канала γ может быть использовано в качестве канала измерения ξ в адаптивной схеме модуляции, то это - канал с замиранием Накагами. Выбор режима вероятности может быть вычислен из формулы:

Где Fc (γ )определяется так:

В канале с замиранием Рэлея при n = 1 вероятность выбора режима задается следующим образом:

Средняя пропускная способность В схемы адаптивной модуляции передачи по каналу с замиранием Накагами задается таким образом:

2.3.8. Фазовая манипуляция m-psk

При использовании фазовой манипуляции в соответствии с символами передаваемого сообщения изменяется фаза гармонического колебания, поэтому передаваемый сигнал можно записать в следующем виде […]:

,

где

;

;

A – амплитуда сигнала; T_S – длительность реализации; φ_k принимает значения из множества ; φ₀ – произвольная начальная фаза.

Сигналы с двоичной фазовой манипуляцией (BPSK)

Рассмотрим сигнал b(t) в виде последовательности импульсов цифровой информации, как это показано на рис.2.12.

Рис. 2.12 ‑ Униполярный и биполярный цифровой сигнал

На верхнем графике показан униполярный цифровой сигнал, в котором информационном логическому нулю соответствует b(t) = 0, а на нижнем графике биполярный цифровой сигнал b₀(t), в котором информационном логическому нулю соответствует b₀(t)= ‑1 .

Подадим биполярный цифровой сигнал в качестве модулирующего сигнала b₀(t) = s_m(t) на фазовый модулятор, как это показано на рис. 2.13 с девиацией фазы равной рад.

Рис.2.13: Формирование BPSK сигнала на основе фазового модулятора

Поскольку b₀(t) принимает только значения равные , то синфазная I(t) и квадратурная Q(t) компоненты комплексной огибающей BPSK сигнала равны:

Тогда BPSK сигнал можно записать:

А структурную схему модулятора можно упростить, как это показано на рис.2.14.

Рис.2.14. Упрощенная структурная схема BPSK модулятора

Рис.2.15. Графики, поясняющие BPSK модулятора

Информация передается со скоростью бит/c, длительность одного импульса цифровой информации равна . Исходный модулирующий сигнал умножается на несущее колебание (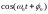 на рисунке ) и получаем фазоманипулированный сигнал со скачком фазы на рад. Таким образом, BPSK модуляция – вырожденный тип фазовой манипуляции, который совпадает с балансной амплитудной модуляцией при биполярном цифровом модулирующем сигнале.

Рассмотрим векторную диаграмму BPSK сигнала. Согласно выражению (1) синфазная компонента I(t) комплексной огибающей BPSK сигнала равна 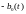, а квадратурная компонента Q(t)=0. При этом принимает значения , тогда векторная диаграмма BPSK сигнала показана на Рис. 2.16.

Рис. 2.16. Векторная диаграмма BPSK сигнала

Вектор комплексной огибающей может принимать одно из двух значений I(t)=1 (при передаче информационного нуля) и I(t)= ‑1 при передаче информационной единицы.

SPECTRUM SENSING METHODS IN COGNITIVE RADIO, A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF Bachelor of Technology In Electronics and Communication Engineering, 2011,43 pages.

SPECTRUM SENSING METHODS IN COGNITIVE RADIO NETWORK,A Thesis Submitted In Partial Fulfillment of The Requirements For The Degree of Bachelor of Technology In Electronics and Communication Engineering, 2014, 45 pages.

Spectrum Sensing Techniques and Issues in Cognitive Radio, International Journal of Engineering Trends and Technology (IJETT) - Volume4Issue4- April 2013.

Sharma, Gaurav, "Adaptive modulation for cognitive radios" (2008). Masters Thses. Paper 6831.