Задание 3.

а1) Найти .

Решение. Применяя подстановку , приведем данный интеграл к табличному интегралу 2. Положим , тогда .

.

а2) Найти .

Применяя подстановку , приведем данный интеграл к формуле 10.

Положим , тогда .

.

б) Найти интеграл .

Преобразуем знаменатель дроби, стоящей под знаком интеграла, следующим образом:

.

Тогда после подстановки получаем

=

=

При этом при вычислении интеграла мы воспользовались заменой переменной . Тогда , откуда

в1) Найти .

Принимаем и ; тогда и , следовательно .

в2) Найти .

Принимаем и ; тогда и . Применяя формулу интегрирования по частям, будем иметь:

в3) Найти .

Принимаем и ; тогда и , следовательно,

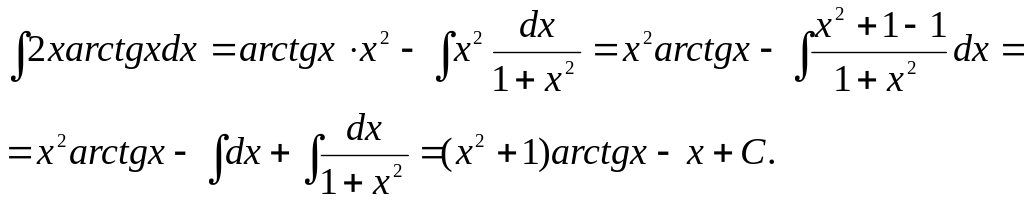
Задание 4.

Вычислить площадь фигуры, ограниченной линиями , (рис. 8).

Решение. Площадь фигуры, ограниченной сверху и снизу непрерывными линиями и , пересекающимися в точках с абсциссами и , определяется по формуле

. (1)

Для нахождения точек пересечения данных линий решаем систему уравнений

Рис. 8

откуда . Применяя формулу (1), получим:

Задание 5.

Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной параболой , прямой и осью Ох.

Решение. Найдем абсциссу точки пересечения параболы и прямой в первом квадранте. Для этого решим уравнение или . Легко убедиться, что , . Первому квадранту соответствует корень .

Найдем теперь абсциссу точки пересечения прямой с осью Ох, решив уравнение , откуда .

Таким образом, можно считать, что тело вращения ограничено при поверхностью, образованной вращением параболы вокруг оси Ох, а при – вращением прямой .

Искомый объем ищем по формуле .

Для вычисления второго интеграла используем подстановку . Тогда и .

Отсюда

.

Задание 6.

Найти объем тела, образованного вращением фигуры , вокруг оси Ох. (Рис. 9)

Решение. По формуле (1), учитывая, что получим

(куб. ед.). Рис. 9

Задание 7.

Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной параболой и прямыми (рис.10).

Решение. По формуле (2), учитывая, что , , получим

(куб. ед.).

Задание 8.

Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, заключенной между линиями , (рис.11).

Решение. Искомый объем определяется разностью , где есть объем тела, образованного вращением вокруг оси Оу треугольника АОВ, а – объем тела, образованного вращением вокруг оси Оу криволинейной трапеции ОтАВ. Чтобы найти пределы интегрирования, найдем ординаты точек пересечения данных линий.

(куб. ед.).

Задание 9.

Исследовать на экстремум функцию

.

Решение. Находим стационарные точки.

Решение последней системы дает 4 стационарные точки:

.

Находим частные производные второго порядка:

Исследуем каждую стационарную точку.

1) В точке Так как и , то в этой точке функция имеет минимум.

2) В точке Так как и , то в этой точке функция имеет максимум.

3) В точке Так как , то в этой точке нет экстремума.

4) В точке Так как , то в этой точке нет экстремума.

Задание 10.

Найти наибольшее и наименьшее значение функции в замкнутом треугольнике АОВ, ограниченном осями координат и прямой (рис. 12).

Решение. Найдем стационарные точки.

Решая систему

находим стационарную точку . Эта точка лежит внутри области. Вычислим значение функции в этой точке.

Граница заданной области состоит из отрезка ОА оси Ох, отрезка ОВ оси Оу и отрезка АВ. Определим наибольшее и наименьшее значение функции на каждом из этих трех участков. На отрезке ОА а . При функция есть функция одной независимой переменной х. Находим наибольшее и наименьшее значение этой функции на отрезке .

; – стационарная точка. .

Вычислим значения функции на концах отрезка ОА, то есть в точках О и А. .

На отрезке ОВ и . При имеем . Находим наибольшее и наименьшее значение этой функции от переменной у на отрезке . ; – стационарная точка. .

Вычислим значения функции на концах отрезка ОВ, то есть в точках О и В. . Исследуем теперь отрезок АВ. Уравнение прямой АВ: . Подставив это выражение для у в заданную функцию , получим или . Определим наибольшее и наименьшее значение этой функции на отрезке .

; – стационарная точка. .

Значения функции в точках А и В найдены ранее. Сравнивая полученные результаты, заключаем, что наибольшее значение заданная функция в заданной замкнутой области достигает в точке , а наименьшее значение – в стационарной точке . Таким образом,

и .